TODO für Tag 18
- Vergleich von Logistic Regression, SVM und RandomForest
Erst mal eine kurze Vorstellung der 3 Algorithmen, auch wenn sie schon in den vorherigen Tagen der 30 Tage scikit-learn Challenge verwendet wurden.
Logistic Regression
Die Logistische Regression ist ein Algorithmus der hauptsächlich für Klassifikationsaufgaben verwendet wird, insbesondere für binäre Klassifikationsprobleme (d.h. Probleme mit zwei möglichen Ergebnissen, z.B. Ja/Nein, 0/1, Spam/Kein Spam). Trotz des Namens „Regression“ im Titel ist das primäre Ziel die Klassifikation.
Ähnlich wie die lineare Regression berechnet sie eine gewichtete Summe der Eingabemerkmale (plus einem Bias-Term). Das Ergebnis dieser linearen Kombination wird dann durch die Sigmoid-Funktion geleitet. Diese Funktion „quetscht“ jeden beliebigen reellen Eingabewert in einen Ausgabewert zwischen 0 und 1. Der Ausgabewert der Sigmoid-Funktion wird als Wahrscheinlichkeit interpretiert, dass die gegebene Eingabe zur positiven Klasse gehört (z.B. Wahrscheinlichkeit für „Ja“ oder „Klasse 1“). Um eine endgültige Klassenzuordnung zu treffen, wird ein Schwellenwert (oft 0.5) verwendet. Liegt die Wahrscheinlichkeit über dem Schwellenwert, wird die Instanz der positiven Klasse zugeordnet, andernfalls der negativen Klasse.
Hier ist ein einfaches Beispiel mit synthetischen Daten:
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
from sklearn.datasets import make_classification # Um Beispieldaten zu generieren
# Daten generieren (synthetische Daten für ein binäres Klassifikationsproblem)
# X sind die Merkmale, y sind die Zielklassen (0 oder 1)
X, y = make_classification(
n_samples=200, # Anzahl der Datenpunkte
n_features=2, # Anzahl der Merkmale (z.B. Größe, Gewicht)
n_informative=2, # Anzahl der informativen Merkmale
n_redundant=0, # Keine redundanten Merkmale
n_clusters_per_class=1, # Wie "gruppiert" die Klassen sind
flip_y=0.1, # Prozentsatz der zufällig "umgedrehten" Labels (Rauschen)
random_state=42 # Für Reproduzierbarkeit
)
# Daten aufteilen in Trainings- und Testsets
# 70% Trainingsdaten, 30% Testdaten
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.3,
random_state=42 # Für Reproduzierbarkeit
)
# Modell instanziieren und trainieren
# solver='liblinear' ist oft eine gute Wahl für kleinere Datensätze und binäre Klassifikation.
# random_state hier für die Reproduzierbarkeit des Solvers, falls er stochastische Elemente hat.
model = LogisticRegression(solver='liblinear', random_state=42)
# Das Modell mit den Trainingsdaten trainieren
model.fit(X_train, y_train)
# Vorhersagen auf dem Testset machen
y_pred = model.predict(X_test)
# Man kann auch die Wahrscheinlichkeiten für jede Klasse vorhersagen:
# y_pred_proba[i][0] ist P(Klasse 0), y_pred_proba[i][1] ist P(Klasse 1)
y_pred_proba = model.predict_proba(X_test)
# Modell evaluieren
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)
print(f"Generierte Merkmale (erste 5 Trainingspunkte):\n{X_train[:5]}")
print(f"Generierte Labels (erste 5 Trainingspunkte):\n{y_train[:5]}\n")
print(f"Genauigkeit des Modells: {accuracy:.4f}")
print("\nKonfusionsmatrix:")
print(conf_matrix)
print("\nKlassifikationsbericht:")
print(class_report)
print("\nBeispiel-Vorhersagen und Wahrscheinlichkeiten (erste 5 Testpunkte):")
for i in range(5):
print(f" Datenpunkt: {X_test[i]}, Wahrscheinlichkeiten: {y_pred_proba[i]}, Vorhergesagte Klasse: {y_pred[i]}, Tatsächliche Klasse: {y_test[i]}")
# Beispiel: Vorhersage für einen neuen, einzelnen Datenpunkt
vorhersage_neu = model.predict(neuer_datenpunkt)
wahrscheinlichkeit_neu = model.predict_proba(neuer_datenpunkt)
print(f"\nVorhersage für neuen Datenpunkt {neuer_datenpunkt[0]}:")
print(f" Vorhergesagte Klasse: {vorhersage_neu[0]}") # Gibt [0] oder [1] zurück
print(f" Wahrscheinlichkeit (Klasse 0, Klasse 1): {wahrscheinlichkeit_neu[0]}")Ausgabe:
Generierte Merkmale (erste 5 Trainingspunkte):
[[ 1.67754452 -1.27723853]
[ 0.42543324 0.69472072]
[ 2.15367981 3.66332221]
[ 0.71376284 -0.44758139]
[ 0.49983212 -1.70707082]]
Generierte Labels (erste 5 Trainingspunkte):
[0 1 1 0 0]
Genauigkeit des Modells: 0.8167
Konfusionsmatrix:
[[28 7]
[ 4 21]]
Klassifikationsbericht:
precision recall f1-score support
0 0.88 0.80 0.84 35
1 0.75 0.84 0.79 25
accuracy 0.82 60
macro avg 0.81 0.82 0.81 60
weighted avg 0.82 0.82 0.82 60
Beispiel-Vorhersagen und Wahrscheinlichkeiten (erste 5 Testpunkte):
Datenpunkt: [0.70366436 0.10497061], Wahrscheinlichkeiten: [0.44506501 0.55493499], Vorhergesagte Klasse: 1, Tatsächliche Klasse: 1
Datenpunkt: [-1.1316811 -1.19667757], Wahrscheinlichkeiten: [0.66076224 0.33923776], Vorhergesagte Klasse: 0, Tatsächliche Klasse: 0
Datenpunkt: [0.54432827 1.10688432], Wahrscheinlichkeiten: [0.19822902 0.80177098], Vorhergesagte Klasse: 1, Tatsächliche Klasse: 0
Datenpunkt: [1.15419481 0.65696708], Wahrscheinlichkeiten: [0.33183872 0.66816128], Vorhergesagte Klasse: 1, Tatsächliche Klasse: 1
Datenpunkt: [-0.0895209 1.83871449], Wahrscheinlichkeiten: [0.08169901 0.91830099], Vorhergesagte Klasse: 1, Tatsächliche Klasse: 0
Vorhersage für neuen Datenpunkt [ 1.5 -0.5]:
Vorhergesagte Klasse: 0
Wahrscheinlichkeit (Klasse 0, Klasse 1): [0.67036277 0.32963723]Mit dem folgenden Python Code kann man die Ergebnisse auch grafisch ausgeben.
if X.shape[1] == 2: # Nur plotten, wenn wir 2 Merkmale haben
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
# Erstelle ein Gitter, um die Entscheidungsgrenze zu plotten
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
# Vorhersagen für jeden Punkt im Gitter machen
# np.c_ verbindet die flachen xx und yy Arrays zu Feature-Paaren
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape) # Zurück in die Gitterform
# Definiere Farbschemata
cmap_light = ListedColormap(['#FFAAAA', '#AAAAFF']) # Helle Farben für Regionen
cmap_bold = ListedColormap(['#FF0000', '#0000FF']) # Kräftige Farben für Punkte
plt.figure(figsize=(10, 7))
# Plot der Entscheidungsgrenze (Regionen)
plt.contourf(xx, yy, Z, cmap=cmap_light, alpha=0.6)
# Plot der Trainingspunkte
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cmap_bold,
edgecolor='k', s=30, marker='o', label='Trainingsdaten')
# Plot der Testpunkte
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cmap_bold,
edgecolor='k', s=100, marker='x', label='Testdaten (Wahr)')
# Optional: Falsch klassifizierte Testpunkte hervorheben
misclassified = (y_test != y_pred)
if np.any(misclassified): # Nur plotten, wenn es Fehlklassifikationen gibt
plt.scatter(X_test[misclassified, 0], X_test[misclassified, 1],
s=150, facecolors='none', edgecolors='lime', linewidths=2,
label='Falsch klassifiziert (Test)')
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title(f"Logistische Regression - Entscheidungsgrenze\nGenauigkeit: {accuracy:.2f}")
plt.xlabel("Merkmal 1")
plt.ylabel("Merkmal 2")
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()
else:
print("\nVisualisierung übersprungen, da mehr als 2 Merkmale vorhanden sind.")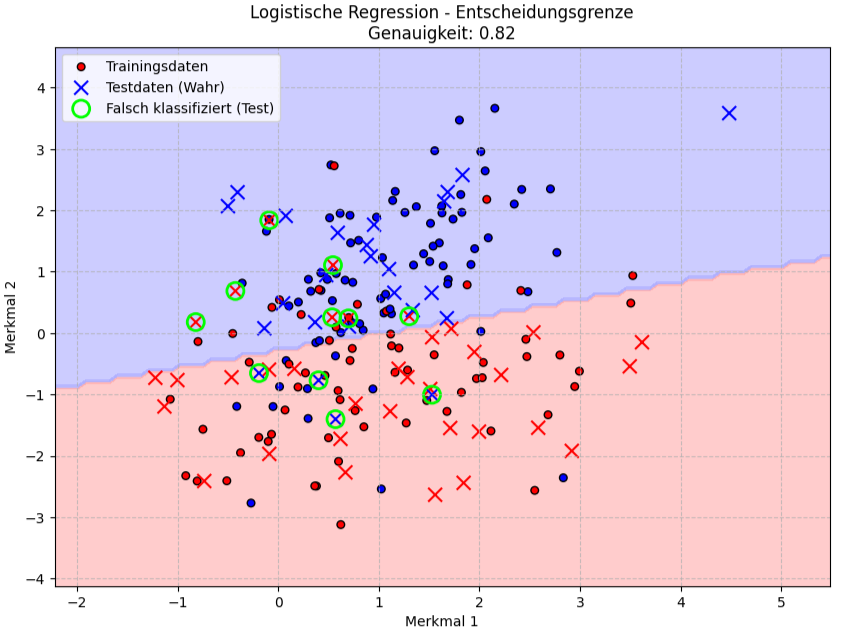
Die Grafik visualisiert die Entscheidungsgrenze eines Logistischen Regressionsmodells für das Klassifikationsproblem mit zwei Merkmalen, „Merkmal 1“ auf der x-Achse und „Merkmal 2“ auf der y-Achse. Die Trainingsdaten sind als kleine, gefüllte Kreise (rot für eine Klasse, blau für die andere) und Testdaten als Kreuze, ebenfalls farblich entsprechend ihrer wahren Klasse kodiert. Zusätzlich sind falsch klassifizierte Testpunkte mit einem grünen Kreis markiert, was aufzeigt, wo das Modell bei den ungesehenen Daten Fehler gemacht hat.
SVM
Support Vector Machines (SVMs) sind ein Verfahren, das sowohl für Klassifikations- als auch für Regressionsaufgaben eingesetzt werden kann. Die grundlegende Idee einer SVM zur Klassifikation besteht darin, eine optimale Trennfläche, eine sogenannte Hyperebene, im Merkmalsraum zu finden, die die Datenpunkte verschiedener Klassen bestmöglich voneinander trennt. Optimal bedeutet hierbei, dass der Abstand, die sogenannte Marge, zwischen der Hyperebene und den nächstgelegenen Datenpunkten jeder Klasse maximiert wird. Diese nächstgelegenen Punkte, welche die Position und Orientierung der Hyperebene maßgeblich bestimmen, werden als Support-Vektoren bezeichnet. Für Daten, die nicht linear trennbar sind, nutzen SVMs den sogenannten Kernel-Trick. Dieser Trick erlaubt es, die Daten implizit in einen höherdimensionalen Raum zu transformieren, in dem eine lineare Trennung möglich wird, ohne diese Transformation explizit berechnen zu müssen. Dies macht SVMs sehr flexibel und effektiv, auch bei komplexen Datensätzen und in hochdimensionalen Räumen.
Beispiel:
from sklearn.svm import SVC # Support Vector Classifier
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 1. Erstelle einen synthetischen Datensatz
# 100 Datenpunkte mit 2 Merkmalen, die zu 2 Klassen gehören.
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)
# 2. Teile Daten in Trainings- und Testsets auf. 80% der Daten zum Trainieren, 20% zum Testen.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 3. Initialisiere und trainiere das SVM-Modell mit linearen Kernel
# C ist der Regularisierungsparameter.
model = SVC(kernel='linear', C=1.0, random_state=42)
# Trainiere das Modell mit den Trainingsdaten
model.fit(X_train, y_train)
# 4. Mache Vorhersagen auf den Testdaten
y_pred = model.predict(X_test)
# 5. Bewerte das Modell
accuracy = accuracy_score(y_test, y_pred)
print(f"Genauigkeit des SVM-Klassifikators: {accuracy:.2f}")Ausgabe:
Genauigkeit des SVM-Klassifikators: 0.95
Eine Genauigkeit von 0.95 bedeutet, dass von allen Datenpunkten im Testset in 95 von 100 Fällen die richtige Klasse zugewiesen wurde. Die restlichen 5% der Vorhersagen waren falsch. Ein Wert von 0.95 (oder 95%) wird im Allgemeinen als eine gute Genauigkeit angesehen, obwohl die Bewertung, ob dies „gut genug“ ist, immer vom spezifischen Anwendungsfall und den damit verbundenen Konsequenzen von Fehlklassifikationen abhängt.
Hier ist ein erweitertes Beispiel, das die Genauigkeit pro Klasse (Recall) berechnet und mit Matplotlib darstellt:
import matplotlib.pyplot as plt
import numpy as np
from sklearn.svm import SVC
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
# Erstelle einen synthetischen Datensatz
# Wir erstellen 100 Datenpunkte mit 2 Merkmalen und diesmal 3 Klassen, um es interessanter zu machen.
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0,
n_classes=3, n_clusters_per_class=1, random_state=42)
# Teile die Daten in Trainings- und Testsets auf
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # 30% zum Testen
# Initialisiere und trainiere das SVM-Modell
# Wir verwenden einen RBF-Kernel, der oft gut für nicht-lineare Probleme ist.
model = SVC(kernel='rbf', C=1.0, gamma='scale', random_state=42)
model.fit(X_train, y_train)
# Mache Vorhersagen auf den Testdaten
y_pred = model.predict(X_test)
# Bewerte das Modell (Gesamtgenauigkeit)
overall_accuracy = accuracy_score(y_test, y_pred)
print(f"Gesamte Genauigkeit des SVM-Klassifikators: {overall_accuracy:.2f}\n")
# Erstelle die Konfusionsmatrix
cm = confusion_matrix(y_test, y_pred)
print("Konfusionsmatrix:")
print(cm)
print("\n")
# Berechne die Genauigkeit (Recall) pro Klasse
per_class_accuracy = cm.diagonal() / cm.sum(axis=1)
# Alternativ: classification_report liefert Precision, Recall, F1-Score pro Klasse
report = classification_report(y_test, y_pred, output_dict=True)
print("Classification Report (Auszug - Recall Werte):")
class_labels = sorted(list(set(y_test))) # Eindeutige Klassenlabels, sortiert
recall_from_report = []
for label in class_labels:
recall_val = report[str(label)]['recall']
recall_from_report.append(recall_val)
print(f" Klasse {label}: Recall = {recall_val:.2f}")
# Sicherstellen, dass unsere manuelle Berechnung mit dem Report übereinstimmt
# (kleine Fließkommaabweichungen sind möglich, aber sollten minimal sein)
assert np.allclose(per_class_accuracy, recall_from_report), "Berechnungen für Recall stimmen nicht überein!"
# Visualisiere die Genauigkeit pro Klasse mit Matplotlib
class_names = [f"Klasse {i}" for i in class_labels]
plt.figure(figsize=(8, 5))
bars = plt.bar(class_names, per_class_accuracy, color=['skyblue', 'lightgreen', 'salmon'])
plt.xlabel("Klasse")
plt.ylabel("Genauigkeit (Recall)")
plt.title("Genauigkeit (Recall) pro Klasse")
plt.ylim(0, 1.05) # Y-Achse bis knapp über 1.0 für bessere Darstellung
# Füge Text mit dem Wert über jeden Balken hinzu
for bar in bars:
yval = bar.get_height()
plt.text(bar.get_x() + bar.get_width()/2.0, yval + 0.01, f'{yval:.2f}', ha='center', va='bottom')
plt.show()Ausgabe:
Gesamte Genauigkeit des SVM-Klassifikators: 0.97
Konfusionsmatrix:
[[11 0 0]
[ 0 11 1]
[ 0 0 7]]
Classification Report (Auszug - Recall Werte):
Klasse 0: Recall = 1.00
Klasse 1: Recall = 0.92
Klasse 2: Recall = 1.00
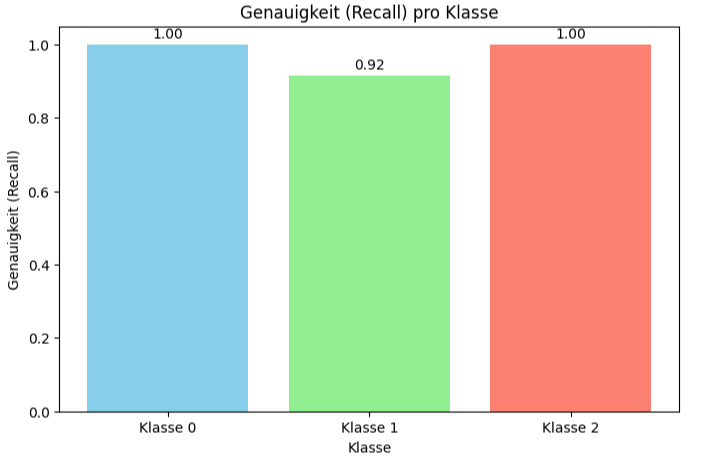
Das Bild visualisiert, wie gut das SVM-Modell darin ist, die Instanzen jeder einzelnen Klasse korrekt zu identifizieren, basierend auf den Testdaten.
Recall (auch Sensitivität oder Trefferquote genannt) misst den Anteil der tatsächlich positiven Instanzen, die korrekt als positiv identifiziert wurden. „pro Klasse“ bedeutet, dass dieser Wert für jede der drei Klassen (Klasse 0, Klasse 1, Klasse 2) einzeln berechnet und dargestellt wird.
Die Y-Achse „Genauigkeit (Recall)“ zeigt den Recall-Wert, der von 0.0 (0%) bis 1.0 (100%) reicht. Ein Wert von 1.0 bedeutet perfekte Identifikation aller Instanzen dieser Klasse.
Die X-Achse „Klasse“ Zeigt die verschiedenen Klassen, für die der Recall berechnet wurde: „Klasse 0“, „Klasse 1“ und „Klasse 2“.
Der Recall für Klasse 0 beträgt 1.00 (oder 100%). Das bedeutet, von allen Datenpunkten, die im Testset tatsächlich zur Klasse 0 gehören, hat das Modell alle korrekt als Klasse 0 erkannt.
Der Recall für Klasse 1 beträgt 0.92 (oder 92%). Das bedeutet, von allen Datenpunkten, die im Testset tatsächlich zur Klasse 1 gehören, hat das Modell 92% korrekt als Klasse 1 erkannt. Die restlichen 8% der tatsächlichen Klasse 1 Instanzen wurden vom Modell anderen Klasse (Klasse 0 oder Klasse 2) zugeordnet.
Der Recall für Klasse 2 beträgt 1.00 (oder 100%). Das bedeutet, ähnlich wie bei Klasse 0 hat das Modell von allen Datenpunkten, die im Testset tatsächlich zur Klasse 2 gehören, alle korrekt als Klasse 2 erkannt.
Diese Art der Darstellung ist nützlich, um zu verstehen, ob das Modell bei bestimmten Klassen möglicherweise Schwächen hat, selbst wenn die Gesamtgenauigkeit (wie die 0.95 aus deiner vorherigen Frage) hoch ist. Es hilft, unausgewogene Leistungen über verschiedene Klassen hinweg zu identifizieren.
RandomForest
Ein Random Forest ist ein Lernverfahren, das auf dem Prinzip der Weisheit der Vielen beruht. Statt sich auf einen einzelnen komplexen Entscheidungsbaum zu verlassen, konstruiert ein Random Forest eine Vielzahl von einzelnen Entscheidungsbäumen während der Trainingsphase. Jeder dieser Bäume wird auf einer leicht unterschiedlichen, zufällig ausgewählten Teilmenge der Trainingsdaten (durch ein Verfahren namens Bootstrapping) und unter Berücksichtigung einer zufälligen Teilmenge der Merkmale an jedem Knotenpunkt trainiert. Diese doppelte Zufälligkeit – sowohl bei den Daten als auch bei den Merkmalen – sorgt für Diversität unter den Bäumen und hilft, Overfitting zu reduzieren.
Bei Klassifikationsaufgaben trifft der Random Forest seine endgültige Vorhersage, indem er die Mehrheitsentscheidung aller einzelnen Bäume heranzieht – quasi eine Abstimmung unter Experten. Für Regressionsaufgaben wird typischerweise der Durchschnitt der Vorhersagen aller Bäume gebildet. Durch die Kombination vieler „schwachen Lerner“, die jeweils auf unterschiedliche Aspekte der Daten spezialisiert sind, entsteht ein robuster und oft sehr genauer „starker Lerner“. Random Forests sind bekannt dafür, gut mit hochdimensionalen Daten umgehen zu können, eine gewisse Resistenz gegenüber Ausreißern aufzuweisen und eine nützliche Einschätzung der Wichtigkeit einzelner Merkmale für die Vorhersage liefern zu können.
Hier ist ein einfaches Beispiel für einen Random Forest Klassifikator mit Matplotlib-Visualisierung der Entscheidungsgrenzen:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification # Zum Erstellen eines Beispieldatensatzes
from sklearn.model_selection import train_test_split # Zum Aufteilen der Daten
from sklearn.metrics import accuracy_score # Zur Bewertung des Modells
# Erstelle einen synthetischen Datensatz
# 200 Datenpunkte mit 2 Merkmalen, die zu 3 Klassen gehören.
# flip_y fügt etwas Rauschen hinzu, um die Klassengrenzen weniger perfekt zu machen.
X, y = make_classification(n_samples=200, n_features=2, n_informative=2, n_redundant=0,
n_classes=3, n_clusters_per_class=1, random_state=42, flip_y=0.1)
# Teile die Daten in Trainings- und Testsets auf
# 70% der Daten zum Trainieren, 30% zum Testen.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Initialisiere und trainiere das Random Forest Modell
# n_estimators: Anzahl der Bäume im Wald.
# max_depth: Maximale Tiefe der Bäume (kann helfen, Overfitting zu kontrollieren)
model = RandomForestClassifier(n_estimators=100, random_state=42, max_depth=5)
# Trainiere das Modell mit den Trainingsdaten
model.fit(X_train, y_train)
# Mache Vorhersagen auf den Testdaten
y_pred = model.predict(X_test)
# Bewerte das Modell
accuracy = accuracy_score(y_test, y_pred)
print(f"Genauigkeit des Random Forest Klassifikators: {accuracy:.2f}")
# Definiere einen Schrittweite für das Gitternetz
h = .02 # Schrittweite im Mesh
# Erstelle Farbkarten
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF']) # Farben für Regionen
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF']) # Farben für Punkte
# Erstelle das Gitternetz für die Visualisierung
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# Mache Vorhersagen für jeden Punkt im Gitternetz
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
# Forme die Vorhersagen in die Gitternetzform um
Z = Z.reshape(xx.shape)
# Erstelle den Plot
plt.figure(figsize=(10, 7))
# Plotte die Entscheidungsgrenzen (Regionen)
plt.contourf(xx, yy, Z, cmap=cmap_light, alpha=0.8)
# Plotte die Trainingspunkte (optional, hier zeigen wir die Testpunkte für eine bessere Beurteilung der Generalisierung)
# plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cmap_bold, edgecolor='k', s=20, label='Trainingsdaten')
# Plotte die Testpunkte
# Wir verwenden `scatter.legend_elements()` um eine Legende für die Klassenfarben zu erstellen
scatter = plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cmap_bold,
edgecolor='k', s=50, marker='o', label='Testdaten (Wahrheit)')
plt.title("Entscheidungsgrenzen des Random Forest")
plt.xlabel("Merkmal 1")
plt.ylabel("Merkmal 2")
# Erstelle eine Legende für die Klassen der Scatter-Punkte
handles, labels = scatter.legend_elements(prop="colors", alpha=0.6)
class_labels = [f'Klasse {i}' for i in range(len(np.unique(y)))] # Erstellt Labels wie 'Klasse 0', 'Klasse 1'
legend_elements = plt.legend(handles, class_labels, title="Klassen", loc="lower right")
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()
# Feature Importances (optional, aber eine Stärke von Random Forests)
importances = model.feature_importances_
feature_names = [f"Merkmal {i+1}" for i in range(X.shape[1])]
sorted_indices = np.argsort(importances)[::-1]
print("\nFeature Importances:")
for i in sorted_indices:
print(f"{feature_names[i]}: {importances[i]:.4f}")
plt.figure(figsize=(8,5))
plt.title("Feature Importances")
plt.bar(range(X.shape[1]), importances[sorted_indices], align="center")
plt.xticks(range(X.shape[1]), np.array(feature_names)[sorted_indices], rotation=45)
plt.tight_layout()
plt.show()Ausgabe:
Genauigkeit des Random Forest Klassifikators: 0.80
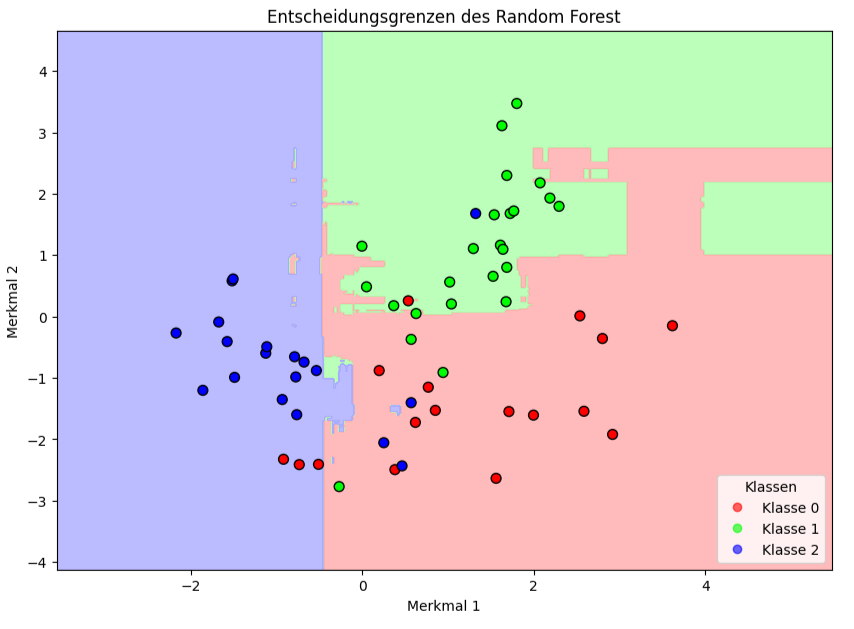
Das Bild zeigt die Entscheidungsgrenzen eines Random Forest Klassifikators für den zweidimensionalen Datensatz des Beispiels mit drei Klassen. Hier ist, was es im Detail aussagt:
Die horizontale Achse („Merkmal 1“) und die vertikale Achse („Merkmal 2“) repräsentieren die beiden Features (Eigenschaften), die verwendet wurden, um die Datenpunkte zu beschreiben und das Modell zu trainieren. Jeder Punkt im Diagramm hat einen Wert für Merkmal 1 und einen für Merkmal 2. Die hellblauen, hellgrünen und hellroten/hellrosa Bereiche sind die Entscheidungsregionen, die vom trainierten Random Forest Modell gelernt wurden.
Die Linien, an denen die farbigen Regionen aufeinandertreffen, sind die Entscheidungsgrenzen. An diesen Grenzen „entscheidet“ sich das Modell, ob ein Punkt zu der einen oder der anderen Klasse gehört. Man sieht, dass die Grenzen nicht glatt sind, sondern eher eine „blockartige“ oder „gestufte“ Struktur haben. Dies ist typisch für baumbasierte Modelle wie Random Forests, da einzelne Entscheidungsbäume Daten durch achsenparallele Schnitte aufteilen. Die Kombination vieler solcher Bäume im Random Forest führt zu diesen komplexeren, aber immer noch oft rechtwinkligen Grenzen. Die farbigen Kreise (rot, grün, blau) stellen die tatsächlichen Datenpunkte aus dem Testdatensatz dar.
Man kann mit dem Plot beurteilen, wie gut die vom Modell gelernten Entscheidungsregionen die tatsächlichen Datenpunkte der verschiedenen Klassen trennen. Die meisten Punkte liegen in der korrekten Region. Wenn ein Punkt einer bestimmten Farbe in einer Region einer anderen Farbe liegt, bedeutet dies eine Fehlklassifikation durch das Modell.
Das Diagramm zeigt, dass Random Forest in der Lage ist, nicht-lineare Beziehungen zwischen den Klassen zu lernen und entsprechend komplexe Entscheidungsgrenzen zu ziehen.
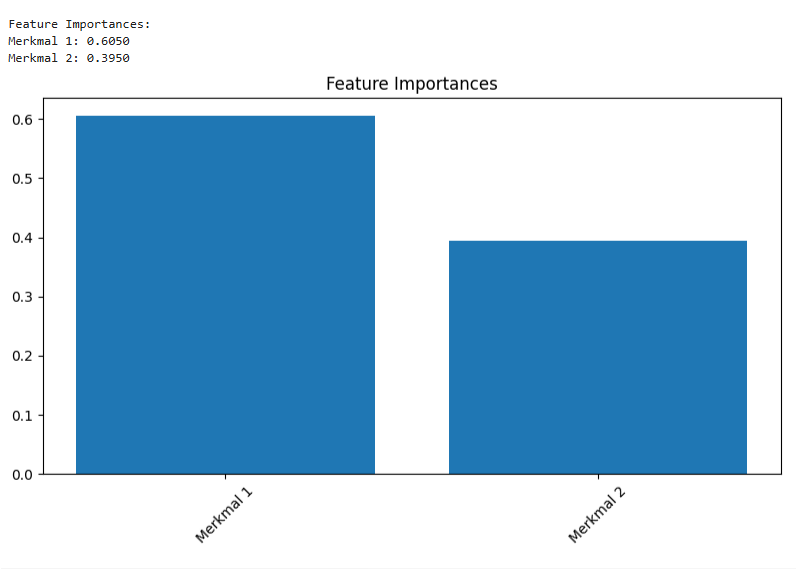
Der 2te Plot visualisiert, wie wichtig jedes einzelne Merkmal (Feature) für die Vorhersagen des trainierten Random Forest Modells war. Er zeigt die relative Bedeutung jedes Eingabemerkmals für die Entscheidungsfindung des Modells darstellt.
Das Diagramm zeigt dass Merkmal 1 für das trainierte Random Forest Modell deutlich wichtiger war als Merkmal 2, um die korrekten Klassenvorhersagen zu treffen. Das Modell hat sich bei seinen Entscheidungen stärker auf die Informationen aus Merkmal 1 gestützt. Mit dieser Grafik kann man Hinweise darauf identifizieren, welche Aspekte der Daten für das zugrundeliegende Problem am aussagekräftigsten sind. In Szenarien mit vielen Features könnte man überlegen, weniger wichtige Merkmale zu entfernen, um das Modell zu vereinfachen und möglicherweise die Trainingszeit zu verkürzen, ohne die Genauigkeit stark zu beeinträchtigen.
Vergleich von Logistic Regression, SVM und RandomForest
Logistic Regression, Support Vector Machines (SVMs) und Random Forests sind drei Algorithmen des maschinellen Lernens, die häufig für Klassifikationsaufgaben eingesetzt werden, obwohl SVMs und Random Forests auch für Regression verwendet werden können. Trotz ihres gemeinsamen Ziels, Datenpunkte Klassen zuzuordnen, unterscheiden sie sich grundlegend in ihrer Funktionsweise, ihren Stärken und den Szenarien, in denen sie typischerweise glänzen.
Die logistische Regression ist ein Modell, das die Wahrscheinlichkeit einer binären Zugehörigkeit (z.B. Klasse 0 oder 1) vorhersagt. Ihre Besonderheit liegt in der Verwendung der Sigmoid-Funktion (oder Logit-Funktion), die eine lineare Kombination der Eingabemerkmale in einen Wahrscheinlichkeitswert zwischen 0 und 1 transformiert. Dieser probabilistische Output ist eine ihrer größten Stärken, da er nicht nur eine Klassenzuordnung, sondern auch ein Maß an Sicherheit für diese Zuordnung liefert. Ihre Einsatzmöglichkeiten sind vielfältig, insbesondere wenn eine klare Interpretation der Modellergebnisse und Wahrscheinlichkeiten erforderlich ist.
Support Vector Machines (SVMs) verfolgen einen anderen Ansatz. Die Kernidee ist es, eine optimale Trennfläche (Hyperebene) im Merkmalsraum zu finden, die den Abstand zu den nächstgelegenen Datenpunkten jeder Klasse maximiert. Diese nächstgelegenen Punkte werden als Support-Vektoren bezeichnet. Eine herausragende Besonderheit der SVM ist der „Kernel-Trick“. Dieser erlaubt es, die Daten implizit in einen höherdimensionalen Raum zu transformieren, in dem eine lineare Trennung möglich wird, auch wenn die Daten im ursprünglichen Raum nicht linear trennbar sind. Gängige Kernel sind der lineare, der polynomiale und der Radial-Basis-Function (RBF) Kernel. SVMs sind besonders effektiv in hochdimensionalen Räumen und wenn die Anzahl der Dimensionen größer ist als die Anzahl der Samples. Sie sind auch relativ speichereffizient, da nur die Support-Vektoren zur Definition der Entscheidungsgrenze herangezogen werden. Die Wahl des richtigen Kernels und die Einstellung der Parameter können jedoch anspruchsvoll sein und erfordern oft sorgfältige Kreuzvalidierung.
Der Random Forest wiederum ist ein Lernverfahren, das auf der Kombination vieler einzelner Entscheidungsbäume basiert. Seine Besonderheit liegt in der Art und Weise, wie diese Bäume konstruiert und kombiniert werden, um die Vorhersagegenauigkeit zu erhöhen und Overfitting zu reduzieren. Jeder Baum wird auf einer zufällig gezogenen Teilmenge der Trainingsdaten trainiert. Zusätzlich wird an jedem Knotenpunkt jedes Baumes nur eine zufällige Untermenge der Merkmale für die Entscheidung über den besten Split in Betracht gezogen. Diese doppelte Zufälligkeit führt zu einer Diversität unter den Bäumen. Für die endgültige Klassifikation wird dann die Mehrheitsentscheidung aller Bäume herangezogen. Random Forests sind bekannt für ihre hohe Genauigkeit, ihre Robustheit gegenüber Ausreißern und Rauschen sowie ihre Fähigkeit, komplexe nicht-lineare Zusammenhänge ohne explizite Transformationen wie den Kernel-Trick der SVMs zu modellieren. Eine weitere Stärke ist die Möglichkeit, die Wichtigkeit einzelner Merkmale (Feature Importance) abzuschätzen, was zur Merkmalsauswahl und zum besseren Verständnis der Daten beitragen kann. Sie sind relativ einfach zu implementieren und erfordern weniger feingranulare Parameteroptimierung als SVMs. Obwohl sie sehr leistungsfähig sind, können sie bei sehr hochdimensionalen und dünn besetzten Daten manchmal weniger gut performen als SVM.
Zusammenfassend lässt sich sagen, dass die logistische Regression durch ihre Einfachheit, Interpretierbarkeit und ihren probabilistischen Output besticht, aber primär für linear trennbare Probleme geeignet ist. SVMs bieten durch den Kernel-Trick eine Methode zur Handhabung nicht-linearer Probleme und hochdimensionaler Daten, erfordern aber sorgfältige Parameterwahl. Random Forests liefern oft eine Vorhersageleistung durch die Aggregation vieler Bäume, sind robust gegenüber Overfitting und bieten Einblicke in die Merkmalswichtigkeit, können aber bei der Interpretation der genauen Entscheidungslogik eine Herausforderung darstellen.
Die Wahl des besten Algorithmus hängt stark von der spezifischen Problemstellung, der Datenbeschaffenheit, dem Bedarf an Interpretierbarkeit und den verfügbaren Rechenressourcen ab.
