TODO für Tag 24
- California Housing Dataset
- Diabetes Dataset
California Housing Dataset
Das California Housing Dataset in scikit-learn ist ein populärer Datensatz, der häufig für Regressionsaufgaben im maschinellen Lernen herangezogen wird. Sein Ziel ist die Vorhersage des Haus-Werts in Kalifornien.
Was diesen Datensatz besonders kennzeichnet und für die Praxis relevant macht, ist seine Natur als Mehrfeature-Datensatz. Das bedeutet, dass die Vorhersage des Hauspreises nicht auf einer einzelnen Eigenschaft basiert, sondern auf einer Kombination verschiedener Merkmale, die jeden geografischen Block beschreiben. Zu diesen Merkmalen gehören beispielsweise das Einkommen der Haushalte in einem Block, das Durchschnittsalter der Häuser, die durchschnittliche Anzahl der Zimmer und Schlafzimmer pro Haushalt, die Bevölkerungsdichte sowie die geografische Lage, ausgedrückt durch Längen- und Breitengrade. Jedes dieser Attribute liefert eine andere Facette an Information, die potenziell den Wert der Immobilien beeinflusst.
Das folgende Beispiel demonstriert, wie man das California Housing Dataset mit scikit-learn laden, ein einfaches Regressionsmodell (Lineare Regression) trainieren und die Ergebnisse mit matplotlib visualisieren können.
Zunächst wird das Dataset geladen. Die Daten werden dann in einen Trainings- und einen Testteil aufgespalten. Das Modell, in diesem Fall eine LinearRegression, lernt ausschließlich auf den Trainingsdaten.
Nach dem Training werden Vorhersagen für die Trainings- als auch die Testdaten generiert. Die Metriken MSE und R² geben eine quantitative Einschätzung der Modellgüte. Ein niedriger MSE und ein R² nahe 1 sind wünschenswert.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# Laden des California Housing Datasets mit as_frame=True, um die Daten direkt als Pandas DataFrame zu erhalten.
housing = fetch_california_housing(as_frame=True)
X = housing.data # Die Features (Eingabevariablen)
y = housing.target # Das Ziel (Medianhauswert = Label für die Vorhersage)
# Einen kurzen Blick auf die Features und das Ziel werfen
print("Form der Features (X):", X.shape)
print("Einige Feature-Namen:", X.columns.tolist())
print("\nForm des Ziels (y):", y.shape)
print("Beispiel Zielwerte (Medianhauspreise in $100,000s):", y.head().values)
print("-" * 30)
# Aufteilen der Daten in Trainings- und Testsets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
print(f"Größe des Trainingsdatensatzes: {X_train.shape[0]} Samples")
print(f"Größe des Testdatensatzes: {X_test.shape[0]} Samples")
print("-" * 30)
# Erstellen und Trainieren des Regressionsmodells
model = LinearRegression()
model.fit(X_train, y_train)
print("Modell trainiert.")
print("-" * 30)
# Vorhersagen auf den Trainings- und Testdaten treffen
y_pred_train = model.predict(X_train)
y_pred_test = model.predict(X_test)
# Mittleren quadratischen Fehler (MSE) und das Bestimmtheitsmaß (R²) ermitteln um das Modell zu Bewerten
mse_train = mean_squared_error(y_train, y_pred_train)
r2_train = r2_score(y_train, y_pred_train)
mse_test = mean_squared_error(y_test, y_pred_test)
r2_test = r2_score(y_test, y_pred_test)
print(f"Trainingsdaten - Mittlerer quadratischer Fehler (MSE): {mse_train:.4f}")
print(f"Trainingsdaten - Bestimmtheitsmaß (R²): {r2_train:.4f}")
print(f"Testdaten - Mittlerer quadratischer Fehler (MSE): {mse_test:.4f}")
print(f"Testdaten - Bestimmtheitsmaß (R²): {r2_test:.4f}")
print("-" * 30)
# Visualisierung der Ergebnisse
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred_test, alpha=0.5, edgecolors='k', s=50)
# Eine Linie für perfekte Vorhersagen (y_test = y_pred_test)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', lw=2)
plt.xlabel("Tatsächliche Medianhauspreise (in $100,000s)")
plt.ylabel("Vorhergesagte Medianhauspreise (in $100,000s)")
plt.title("Tatsächliche vs. Vorhergesagte Hauspreise (Testdaten)")
plt.grid(True)
plt.show()
# Residuenplot für das Testset
# Residuen sind die Differenz zwischen tatsächlichen und vorhergesagten Werten.
residuals_test = y_test - y_pred_test
plt.figure(figsize=(10, 6))
plt.scatter(y_pred_test, residuals_test, alpha=0.5, edgecolors='k', s=50)
plt.hlines(0, y_pred_test.min(), y_pred_test.max(), colors='r', linestyles='--') # Nulllinie
plt.xlabel("Vorhergesagte Medianhauspreise (in $100,000s)")
plt.ylabel("Residuen (Tatsächlich - Vorhergesagt)")
plt.title("Residuenplot (Testdaten)")
plt.grid(True)
plt.show()
# Verteilung der Residuen
plt.figure(figsize=(10, 6))
plt.hist(residuals_test, bins=50, edgecolor='k', alpha=0.7)
plt.xlabel("Residuen")
plt.ylabel("Häufigkeit")
plt.title("Verteilung der Residuen (Testdaten)")
plt.grid(axis='y', alpha=0.75)
plt.show()Ausgabe:
Form der Features (X): (20640, 8)
Einige Feature-Namen: ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude']
Form des Ziels (y): (20640,)
Beispiel Zielwerte (Medianhauspreise in $100,000s): [4.526 3.585 3.521 3.413 3.422]
------------------------------
Größe des Trainingsdatensatzes: 16512 Samples
Größe des Testdatensatzes: 4128 Samples
------------------------------
Modell trainiert.
------------------------------
Trainingsdaten - Mittlerer quadratischer Fehler (MSE): 0.5179
Trainingsdaten - Bestimmtheitsmaß (R²): 0.6126
Testdaten - Mittlerer quadratischer Fehler (MSE): 0.5559
Testdaten - Bestimmtheitsmaß (R²): 0.5758
------------------------------
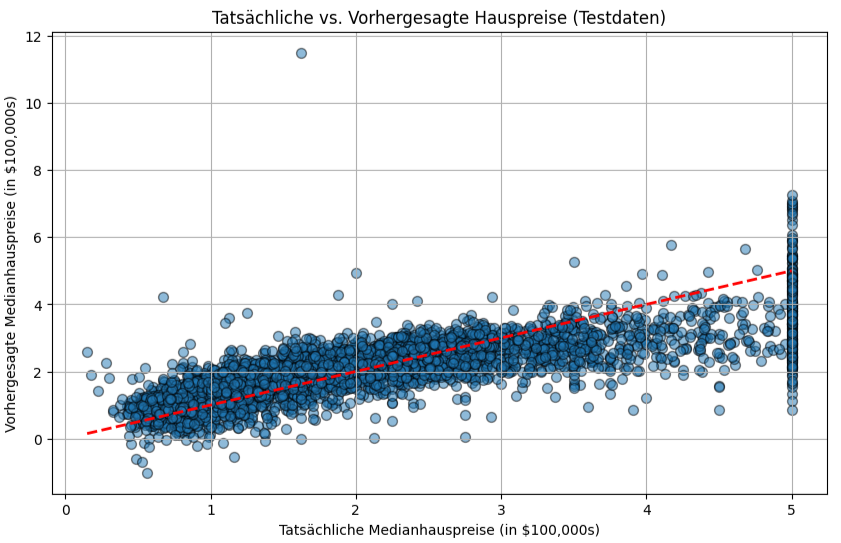
Die erste Visualisierung zeigt ein Streudiagramm der tatsächlichen Medianhauspreise gegen die vom Modell vorhergesagten Preise für das Testset. Punkte, die nahe an der roten diagonalen Linie liegen, deuten auf gute Vorhersagen hin. Eine starke Streuung um diese Linie herum signalisiert Bereiche, in denen das Modell ungenauer ist.
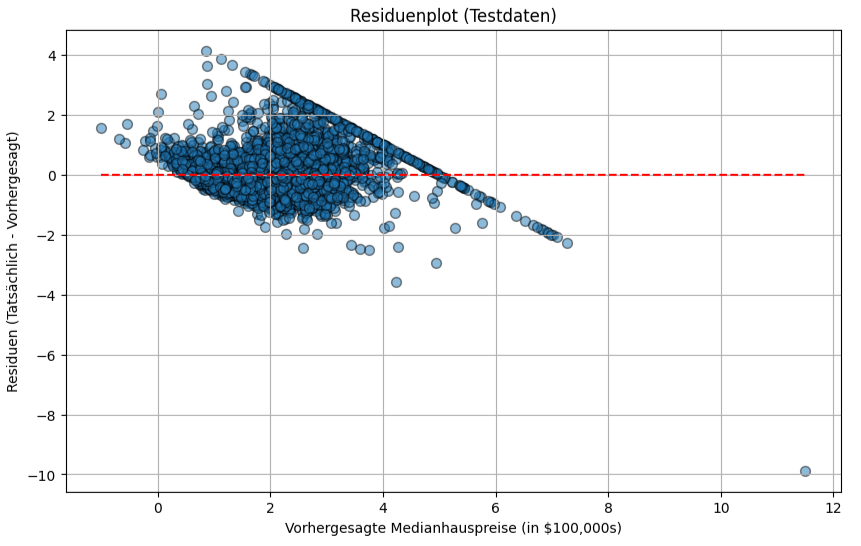
Der Residuenplot, stellt die Differenzen zwischen tatsächlichen und vorhergesagten Werten (die Residuen) gegen die vorhergesagten Werte dar. Idealerweise sollten die Residuen zufällig um die Nulllinie streuen, ohne erkennbare Muster. Muster in diesem Plot könnten darauf hindeuten, dass das lineare Modell nicht alle Zusammenhänge in den Daten erfasst oder dass die Varianz der Fehler nicht konstant ist.
Als Residuen bezeichnet man die Differenz zwischen dem tatsächlichen, wahren Wert und dem Wert, den das Modell vorhergesagt hat. Für jeden einzelnen Datenpunkt berechnet man das Residuum nach der Formel: Residuum = tatsächlicher Wert – vorhergesagter Wert. Ein kleines Residuum bedeutet, dass die Vorhersage gut war, während ein großes Residuum (egal ob positiv oder negativ) auf eine ungenaue Vorhersage hindeutet.
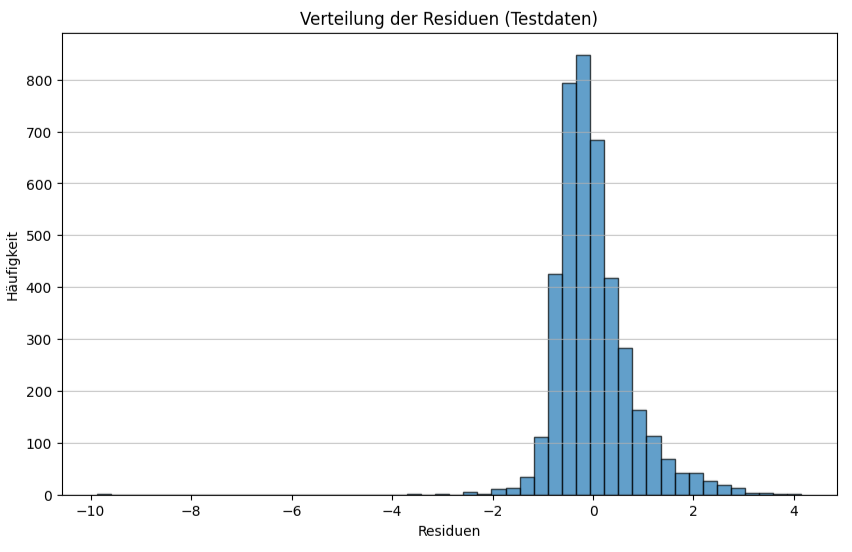
Der dritte Plot zeigt ein Histogramm der Residuen. Bei einem gut angepassten Modell würden wir erwarten, dass die Residuen ungefähr normalverteilt sind und sich um 0 zentrieren. Dies gibt einen weiteren Hinweis darauf, ob die Annahmen des linearen Regressionsmodells erfüllt sind.
Tauscht man die Zeile model = LinearRegression() durch die Zeile model = RandomForestRegressor(); aus, sieht die Ausgabe wie folgt aus.
Form der Features (X): (20640, 8)
Einige Feature-Namen: ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude']
Form des Ziels (y): (20640,)
Beispiel Zielwerte (Medianhauspreise in $100,000s): [4.526 3.585 3.521 3.413 3.422]
------------------------------
Größe des Trainingsdatensatzes: 16512 Samples
Größe des Testdatensatzes: 4128 Samples
------------------------------
Modell trainiert.
------------------------------
Trainingsdaten - Mittlerer quadratischer Fehler (MSE): 0.0356
Trainingsdaten - Bestimmtheitsmaß (R²): 0.9734
Testdaten - Mittlerer quadratischer Fehler (MSE): 0.2550
Testdaten - Bestimmtheitsmaß (R²): 0.8054
------------------------------
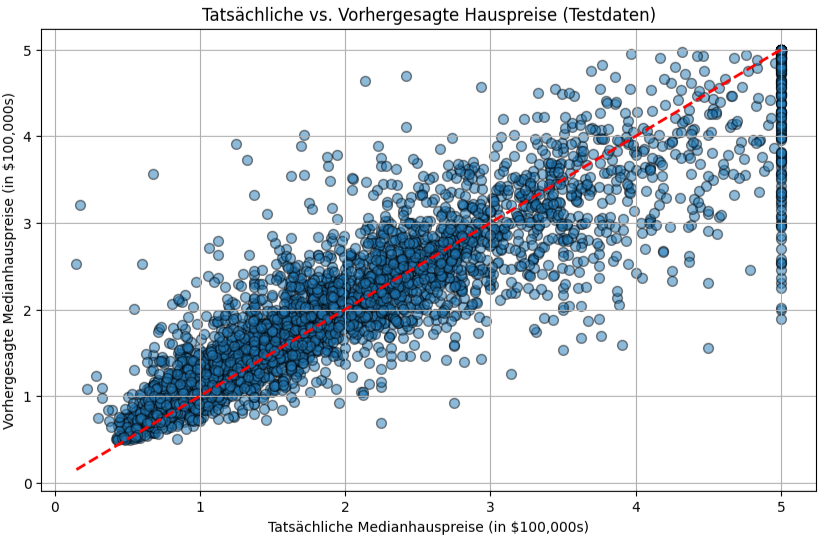
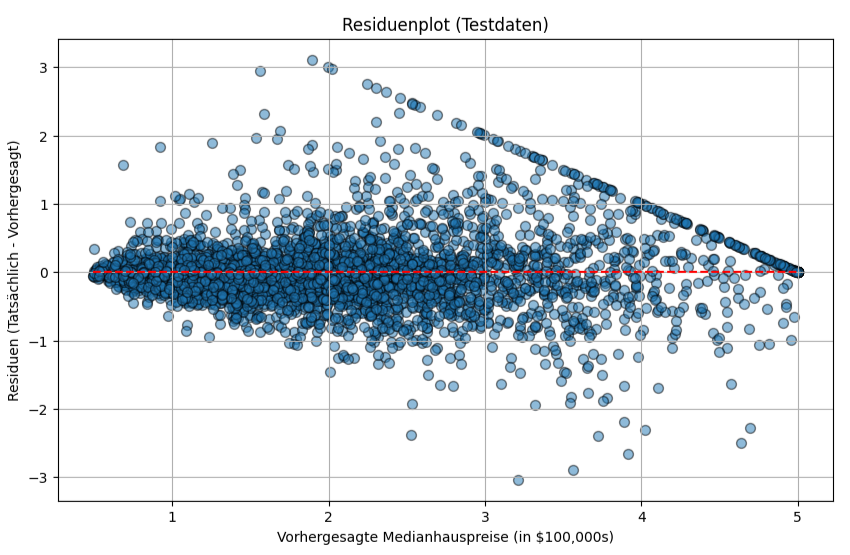
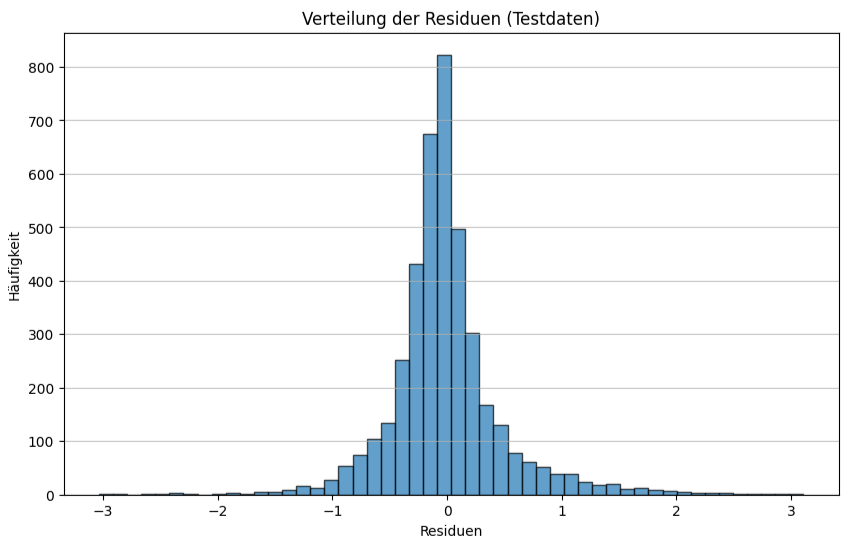
Wie man sieht, ist der RandomForestRegressor deutlich besser, darin die Hauspreise vorherzusagen. Währende die LinearRegression bei den Testdaten einen MSE von 0.5559 und einen R² von 0.5758 hat, kann der RandomForestRegressor auf den Testdateneinen MSE von 0.2550 und einen R² von 0.8054 erreichen.
- MSE (Mittlerer quadratischer Fehler / Mean Squared Error)
- LinearRegression: 0.5559
- RandomForestRegressor: 0.2550
Ein niedrigerer MSE ist besser, da er den durchschnittlichen quadrierten Unterschied zwischen den vorhergesagten und den tatsächlichen Werten angibt. Der RandomForestRegressor hat einen MSE, der weniger als halb so groß ist wie der der LinearRegression. Das bedeutet, dass seine Vorhersagen im Durchschnitt deutlich näher an den wahren Hauspreisen liegen.
- R² (Bestimmtheitsmaß / R-squared):
- LinearRegression: 57,58%
- RandomForestRegressor: 80,54%
Ein höherer R²-Wert ist besser. Er gibt an, welcher Anteil der Varianz der Hauspreise durch das Modell erklärt werden kann. Der RandomForestRegressor kann etwa 80,5% der Schwankungen in den Hauspreisen erklären, während die LinearRegression nur etwa 57,6% erklären kann.
Zusammenfassend bedeutet es, dass das RandomForestRegressor-Modell präzisere Vorhersagen liefert und ein besseres Verständnis bzw. eine bessere Erklärung für die Preisbildung aufweist als das LinearRegression-Modell, wenn es um die Vorhersage der Hauspreise auf den Testdaten geht.
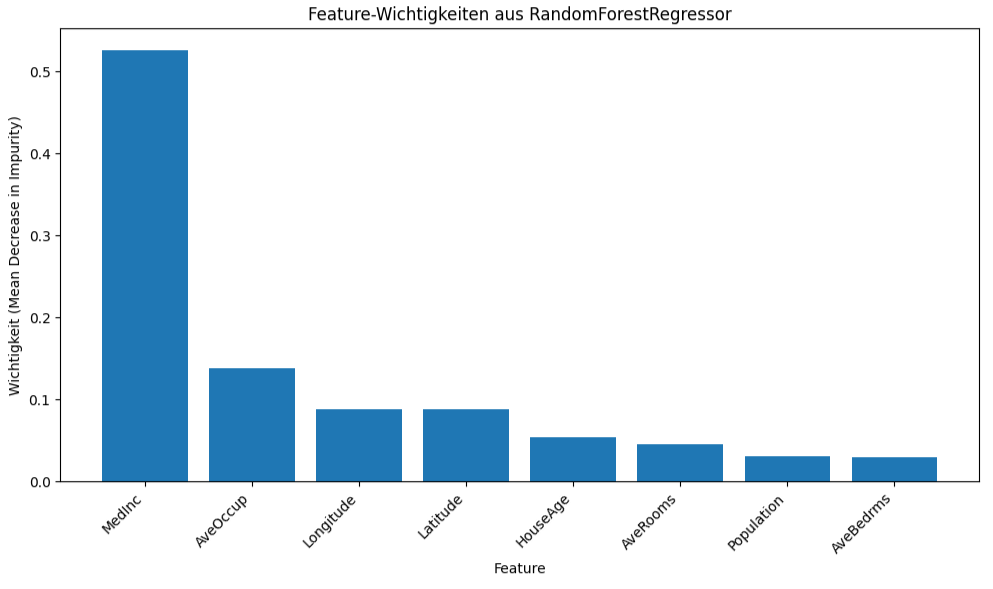
Mit dem folgenden Code-Snippet kann man sich die Wichtigkeit der Features anzeigen lassen.
importances = model.feature_importances_
# Wichtigkeiten mit Feature-Namen kombinieren und sortieren
feature_importance_df = pd.DataFrame({'feature': X.columns.tolist(), 'importance': importances})
feature_importance_df = feature_importance_df.sort_values('importance', ascending=False)
print("Feature-Wichtigkeiten (MDI):")
print(feature_importance_df)
# Visualisierung der Feature-Wichtigkeiten
plt.figure(figsize=(10, 6))
plt.bar(feature_importance_df['feature'], feature_importance_df['importance'])
plt.xlabel("Feature")
plt.ylabel("Wichtigkeit (Mean Decrease in Impurity)")
plt.title("Feature-Wichtigkeiten aus RandomForestRegressor")
plt.xticks(rotation=45, ha="right") # Feature-Namen lesbar machen
plt.tight_layout() # Stellt sicher, dass alles gut in den Plot passt
plt.show()
# Beispiel für Permutationswichtigkeit (optional, aber oft besser)
from sklearn.inspection import permutation_importance
print("\nBerechne Permutationswichtigkeit (kann etwas dauern)...")
perm_importance_result = permutation_importance(
model, X_test, y_test, n_repeats=10, random_state=42, n_jobs=-1
)
sorted_idx = perm_importance_result.importances_mean.argsort()[::-1] # Indizes für Sortierung (absteigend)
perm_feature_importance_df = pd.DataFrame({
'feature': X_test.columns[sorted_idx],
'importance_mean': perm_importance_result.importances_mean[sorted_idx],
'importance_std': perm_importance_result.importances_std[sorted_idx]
})
print("\nFeature-Wichtigkeiten (Permutation Importance):")
print(perm_feature_importance_df)
plt.figure(figsize=(10, 6))
plt.bar(perm_feature_importance_df['feature'], perm_feature_importance_df['importance_mean'],
yerr=perm_feature_importance_df['importance_std']) # Fehlerbalken hinzufügen
plt.xlabel("Feature")
plt.ylabel("Wichtigkeit (Permutation Importance - Mean Decrease in R² or Score)")
plt.title("Feature-Wichtigkeiten (Permutation) aus RandomForestRegressor")
plt.xticks(rotation=45, ha="right")
plt.tight_layout()
plt.show()Ausgabe:
Feature-Wichtigkeiten (MDI):
feature importance
0 MedInc 0.526144
5 AveOccup 0.138454
7 Longitude 0.087853
6 Latitude 0.087563
1 HouseAge 0.054115
2 AveRooms 0.045319
4 Population 0.030988
3 AveBedrms 0.029564
Berechne Permutationswichtigkeit (kann etwas dauern)...
Feature-Wichtigkeiten (Permutation Importance):
feature importance_mean importance_std
0 MedInc 0.742168 0.014654
1 Latitude 0.425746 0.008955
2 Longitude 0.327064 0.006014
3 AveOccup 0.201939 0.005184
4 HouseAge 0.071930 0.003659
5 AveRooms 0.028868 0.001917
6 AveBedrms 0.009511 0.001866
7 Population 0.007912 0.001041
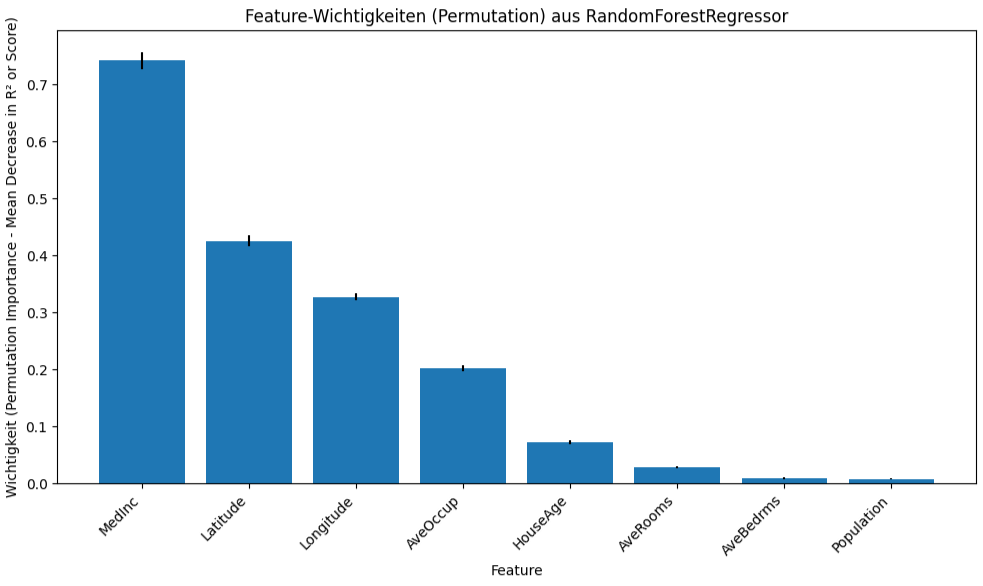
Das Medianeinkommen ist der mit Abstand stärkste Prädiktor für Hauspreise in diesem Modell, gefolgt von der geografischen Lage (Breiten- und Längengrad) und der durchschnittlichen Belegung. Das Alter der Häuser spielt eine geringere, aber immer noch messbare Rolle, während die durchschnittliche Zimmer-/Schlafzimmeranzahl und die Bevölkerungsdichte in den Blöcken laut dieser Analyse den geringsten Einfluss auf die Vorhersagen des Modells haben.
Diabetes Dataset
Der Diabetes-Datensatz ist ein Datensatz, der für Regressionsaufgaben im maschinellen Lernen verwendet wird. Er enthält Messwerte von Diabetes-Patienten, mit dem Ziel, die Krankheitsprogression ein Jahr nach der Baseline-Messung vorherzusagen. Der Diabetes-Datensatz enthält folgende Informationen.
- Anzahl der Beobachtungen (Samples): 442 Patienten
- Anzahl der Merkmale (Features): 10
- Zielvariable: Eine quantitative Messung der Krankheitsprogression ein Jahr nach der ersten Erhebung. Es ist ein kontinuierlicher Wert.
Alle 10 Merkmale wurden mittelwertzentriert und skaliert, sodass die Summe der Quadrate jeder Spalte 1 beträgt. Dies Form der Standardisierung ist für viele Algorithmen vorteilhaft.
- target: Dies ist die quantitative Messung der Krankheitsprogression ein Jahr nach der ersten Erhebung. Höhere Werte deuten auf eine stärkere Progression der Krankheit hin.
Beschreibung der Merkmale (Features):
Die zehn Basislinienvariablen sind Alter, Geschlecht, Body-Mass-Index, durchschnittlicher Blutdruck und sechs Bläserum-Messungen.
- age (Alter)
Beschreibung: Das Alter des Patienten in Jahren.
Einheit: Jahre (vor der Skalierung). - sex (Geschlecht)
Beschreibung: Das Geschlecht des Patienten. Im ursprünglichen Datensatz wurde dies wahrscheinlich als kategoriale Variable erfasst und dann numerisch kodiert, bevor es skaliert wurde. Scikit-learn liefert direkt die skalierten numerischen Werte. - bmi (Body-Mass-Index)
Beschreibung: Ein Maß zur Bewertung des Körpergewichts einer Person in Relation zu ihrer Körpergröße.
Einheit: kg/m ² (vor der Skalierung). - bp (Average Blood Pressure – Durchschnittlicher Blutdruck)
Beschreibung: Der mittlere arterielle Blutdruck (MAP).
Einheit: mmHg (Millimeter Quecksilbersäule) (vor der Skalierung). - s1 (tc – Total Serum Cholesterol)
Beschreibung: Gesamtcholesterin im Serum. Ein Blutfettwert.
Einheit: mg/dL (Milligramm pro Deziliter) (vor der Skalierung). - s2 (ldl – Low-Density Lipoproteins)
Beschreibung: Low-Density Lipoproteine, oft als „schlechtes Cholesterin“ bezeichnet.
Einheit: mg/dL (vor der Skalierung). - s3 (hdl – High-Density Lipoproteins)
Beschreibung: High-Density Lipoproteine, oft als „gutes Cholesterin“ bezeichnet.
Einheit: mg/dL (vor der Skalierung). - s4 (tch – Total Cholesterol / HDL ratio oder auch Thyroid Stimulating Hormone)
Beschreibung: Die LARS-Originalarbeit listet „tch“ als Thyroid Stimulating Hormone.
Einheit: Quotient oder Konzentration (vor der Skalierung). - s5 (ltg – Possibly Log of Serum Triglycerides level)
Beschreibung: Scikit-learn „possibly log of serum triglycerides level“.
Einheit: mg/dL (für Triglyceride, vor Logarithmierung und Skalierung). - s6 (glu – Blood Sugar Level)
Beschreibung: Der Blutzuckerspiegel, ein zentraler Wert bei Diabetes.
Einheit: mg/dL (vor der Skalierung).
Der Diabetes-Datensatz bietet eine gute Grundlage, um Regressionsmodelle zu testen und zu verstehen. Die Merkmale sind bereits vorverarbeitet (skaliert), was die direkte Anwendung vieler Algorithmen erleichtert. Es ist jedoch wichtig, sich der Bedeutung der ursprünglichen Messgrößen und der durchgeführten Skalierung bewusst zu sein, insbesondere bei der Interpretation der Modellergebnisse oder der Feature-Importances.
Mit folgendendem Code kann man einen RandomForestRegressor trainieren und die Permutationswichtigkeit plotten.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.inspection import permutation_importance
from sklearn.metrics import r2_score
# Diabetes Datensatz laden
diabetes = load_diabetes()
X, y = diabetes.data, diabetes.target
feature_names = diabetes.feature_names
# Daten aufteilen in Trainings- und Testsets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# RandomForestRegressor Modell initialisieren und trainieren
model = RandomForestRegressor(n_estimators=100, random_state=42, n_jobs=-1) # n_jobs=-1 nutzt alle Prozessorkerne
model.fit(X_train, y_train)
# Modellleistung auf dem Testset bewerten
y_pred_test = model.predict(X_test)
r2_test = r2_score(y_test, y_pred_test)
print(f"R²-Wert des RandomForestRegressor auf dem Testset: {r2_test:.4f}")
# Permutationswichtigkeit berechnen
perm_importance_result = permutation_importance(
model, X_test, y_test, scoring='r2', n_repeats=10, random_state=42, n_jobs=-1
)
# Die Ergebnisse enthalten importances_mean, importances_std und importances (für jede Wiederholung)
importances_mean = perm_importance_result.importances_mean
importances_std = perm_importance_result.importances_std
# Feature-Wichtigkeiten für die Visualisierung sortieren
sorted_idx = importances_mean.argsort() # Gibt die Indizes zurück, die die Werte sortieren würden
# Permutationswichtigkeit plotten
plt.figure(figsize=(12, 8))
plt.barh(
np.array(feature_names)[sorted_idx],
importances_mean[sorted_idx],
xerr=importances_std[sorted_idx], # Fügt Fehlerbalken basierend auf der Standardabweichung hinzu
capsize=5, # Größe der Kappen der Fehlerbalken
color="skyblue"
)
plt.xlabel("Permutationswichtigkeit (Abnahme im R²-Score)")
plt.ylabel("Feature")
plt.title("Permutationswichtigkeit der Features für den Diabetes Datensatz\n(RandomForestRegressor)")
plt.gca().invert_yaxis() # Optional: Wichtigstes Feature oben anzeigen
plt.tight_layout() # Stellt sicher, dass alles gut in die Abbildung passt
plt.show()
print("\nDurchschnittliche Permutationswichtigkeit (Abnahme im R²-Score):")
for i in sorted_idx[::-1]: # Umgekehrt sortiert, wichtigstes zuerst
print(f"{feature_names[i]:<5}: {importances_mean[i]:.4f} +/- {importances_std[i]:.4f}")Ausgabe:
R²-Wert des RandomForestRegressor auf dem Testset: 0.4428
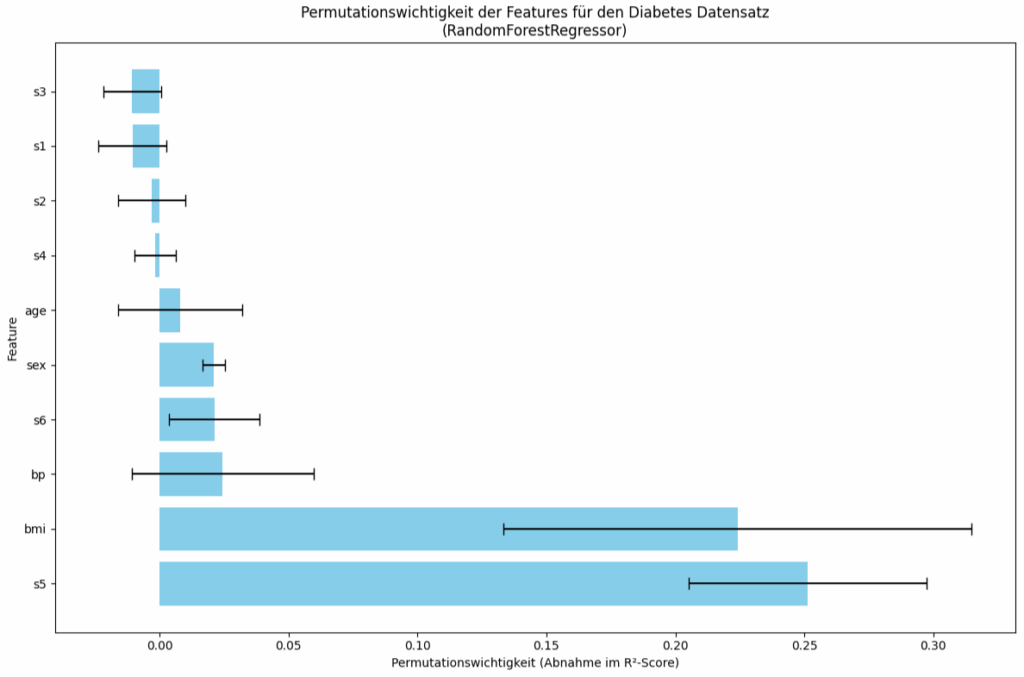
Das Bild zeigt die Permutationswichtigkeit der Features für den scikit-learn Diabetes Datensatz darstellt, ermittelt mit einem RandomForestRegressor.
Die Permutationswichtigkeit misst den Rückgang der Modellgüte (R²-Score), wenn die Werte eines einzelnen Features zufällig permutiert werden. Die Länge jedes Balkens repräsentiert die durchschnittliche Permutationswichtigkeit des entsprechenden Features. Längere Balken bedeuten höhere Wichtigkeit.
Die Schwarze horizontale Linien (Fehlerbalken) an den Enden der Balken stellen die Standardabweichung der Wichtigkeitswerte über die (wahrscheinlich mehrfachen) Wiederholungen der Permutation dar. Längere Fehlerbalken deuten auf eine größere Variabilität oder Unsicherheit in der Schätzung der Wichtigkeit hin.
Das Feature s5 Ist mit Abstand das wichtigste Feature. Die Permutation dieses Features führt zur größten Abnahme des R²-Scores (ca. 0.25). Allerdings ist der Fehlerbalken relativ lang, was auf eine gewisse Variabilität hindeutet, aber es bleibt das dominanteste Merkmal. Die Bedeutung von s5 ist „Possibly Log of Serum Triglycerides level„. Dem Mediziner wird das was sagen, aber ich habe keine Ahnung ….
Das Feature bmi ist das zweitwichtigste Feature. Die Abnahme des R²-Scores ist immer noch beträchtlich (ca. 0.22), aber geringer als bei s5. Auch hier ist der Fehlerbalken recht ausgeprägt. Unter dem bmi (Body-Mass-Index) kann ich mir eher was vorstellen und es ist auch klar, warum dieses Feature so wichtig ist.
Alle anderen Features haben deutlich geringeren Einfluss auf den R²-Score. Die Abnahme liegt bei unter 0.025 pro Feature. Das Modell stützt sich bei seinen Vorhersagen also primär auf s5 und bmi. Eine zweite Gruppe von Features (bp, s6, sex, age) trägt noch in geringerem Maße zur Vorhersage bei. Die restlichen Features (s4, s2, s1, s3) scheinen für dieses spezifische RandomForestRegressor-Modell kaum relevant zu sein, da ihre Permutation die Vorhersagegüte kaum verschlechtert. Die Fehlerbalken geben einen Hinweis auf die Stabilität der Wichtigkeitsschätzung. Bei Features wie bmi und s5 gibt es trotz ihrer hohen mittleren Wichtigkeit eine gewisse Schwankungsbreite.
