TODO für Tag 26
- Umgang mit unbalancierten Klassen (z.B. class_weight, SMOTE mit externen Bibliotheken)
Umgang mit unbalancierten Klassen (class_weight)
In scikit-learn wird der Parameter class_weight in vielen Klassifikationsalgorithmen (wie z.B. LogisticRegression, SVC, DecisionTreeClassifier, RandomForestClassifier) verwendet, um mit unbalancierten Klassen umzugehen. Die Grundidee ist, den Loss beim Training des Modells für die unterrepräsentierte(n) Klasse(n) höher zu gewichten.
Wenn z.B. eine Klasse deutlich mehr Instanzen hat als andere (z.B. 90% Klasse A, 10% Klasse B), neigen viele Algorithmen dazu, die Mehrheitsklasse übermäßig gut zu lernen und die Minderheitsklasse zu ignorieren. Das liegt daran, dass der Standard-Loss-Funktion jeder Fehler gleich viel „kostet“. Ein Modell, das einfach immer die Mehrheitsklasse vorhersagt, hätte bereits eine hohe Accuracy, aber eine schlechte Leistung für die Minderheitsklasse.
Um dem Problem zu begegnen, gibt es den Parameter class_weight. Er passt die Loss-Funktion an, indem die Fehlklassifikationen von Instanzen der Minderheitsklasse stärker bestraft. Wenn eine Instanz der Minderheitsklasse falsch klassifiziert wird, trägt dieser Fehler mit einem höheren Gewicht zum Gesamtverlust bei, den der Algorithmus während des Trainings zu minimieren versucht.
Während des Trainings wird also der Beitrag jeder einzelnen Instanz zum Gesamtverlust mit dem Gewicht ihrer Klasse multipliziert. Wenn also ein Sample der Klasse a mit Gewicht w falsch klassifiziert wird, ist der „Schaden“ für die Loss-Funktion w * loss_für_dieses_sample anstatt nur loss_für_dieses_sample. Das Modell wird versuchen, diese gewichteten Verluste zu minimieren, was implizit bedeutet, dass es stärker darauf achtet, die hoch gewichteten Minderheitsklassen korrekt zu klassifizieren. So kann die Performance für Minderheitsklassen signifikant verbessert werden. Der Parameter class_weight beeinflusst hier nur den Trainingsprozess. Die Vorhersagen selbst werden nicht direkt gewichtet.
Beispiel:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import (
classification_report,
confusion_matrix,
roc_auc_score,
roc_curve,
precision_recall_fscore_support
)
from collections import Counter
# Erstellen eines unbalancierten Datensatzes
X, y = make_classification(n_samples=10000, n_features=20, n_informative=15,
n_redundant=5, n_classes=2, weights=[0.95, 0.05],
flip_y=0.05, random_state=42)
print(f"Verteilung der Klassen im gesamten Datensatz: {Counter(y)}")
# Aufteilen in Trainings- und Testdaten
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
print(f"Verteilung der Klassen im Trainingsdatensatz: {Counter(y_train)}")
print(f"Verteilung der Klassen im Testdatensatz: {Counter(y_test)}")
print("-" * 50)
# Modelltraining OHNE class_weight
model_ohne_cw = LogisticRegression(solver='liblinear', random_state=42)
model_ohne_cw.fit(X_train, y_train)
y_pred_ohne_cw = model_ohne_cw.predict(X_test)
y_proba_ohne_cw = model_ohne_cw.predict_proba(X_test)[:, 1]
print("\nClassification Report (OHNE class_weight):")
report_ohne_cw = classification_report(y_test, y_pred_ohne_cw, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)'], output_dict=True)
print(classification_report(y_test, y_pred_ohne_cw, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)']))
cm_ohne_cw = confusion_matrix(y_test, y_pred_ohne_cw)
auc_ohne_cw = roc_auc_score(y_test, y_proba_ohne_cw)
print(f"ROC AUC Score (OHNE class_weight): {auc_ohne_cw:.4f}")
print("-" * 50)
# Modelltraining MIT class_weight='balanced'
model_mit_cw = LogisticRegression(solver='liblinear', random_state=42, class_weight='balanced')
model_mit_cw.fit(X_train, y_train)
y_pred_mit_cw = model_mit_cw.predict(X_test)
y_proba_mit_cw = model_mit_cw.predict_proba(X_test)[:, 1]
print("\nClassification Report (MIT class_weight='balanced'):")
report_mit_cw = classification_report(y_test, y_pred_mit_cw, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)'], output_dict=True)
print(classification_report(y_test, y_pred_mit_cw, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)']))
cm_mit_cw = confusion_matrix(y_test, y_pred_mit_cw)
auc_mit_cw = roc_auc_score(y_test, y_proba_mit_cw)
print(f"ROC AUC Score (MIT class_weight='balanced'): {auc_mit_cw:.4f}")
print("-" * 50)
# Visualisierungen
target_names = ['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)']
# Confusion Matrices
fig, axes = plt.subplots(1, 2, figsize=(14, 5))
sns.heatmap(cm_ohne_cw, annot=True, fmt='d', cmap='Blues', ax=axes[0],
xticklabels=target_names, yticklabels=target_names)
axes[0].set_title('Confusion Matrix (Ohne class_weight)')
axes[0].set_xlabel('Vorhergesagte Klasse')
axes[0].set_ylabel('Tatsächliche Klasse')
sns.heatmap(cm_mit_cw, annot=True, fmt='d', cmap='Greens', ax=axes[1],
xticklabels=target_names, yticklabels=target_names)
axes[1].set_title('Confusion Matrix (Mit class_weight="balanced")')
axes[1].set_xlabel('Vorhergesagte Klasse')
axes[1].set_ylabel('Tatsächliche Klasse')
plt.tight_layout()
plt.show()
# Balkendiagramm für Metriken der Minderheitsklasse
metrics_ohne = [
report_ohne_cw['Klasse 1 (Minderheit)']['precision'],
report_ohne_cw['Klasse 1 (Minderheit)']['recall'],
report_ohne_cw['Klasse 1 (Minderheit)']['f1-score']
]
metrics_mit = [
report_mit_cw['Klasse 1 (Minderheit)']['precision'],
report_mit_cw['Klasse 1 (Minderheit)']['recall'],
report_mit_cw['Klasse 1 (Minderheit)']['f1-score']
]
metric_names = ['Precision', 'Recall', 'F1-Score']
x = np.arange(len(metric_names)) # die Label-Positionen
width = 0.35 # die Breite der Balken
fig, ax = plt.subplots(figsize=(10, 6))
rects1 = ax.bar(x - width/2, metrics_ohne, width, label='Ohne class_weight', color='skyblue')
rects2 = ax.bar(x + width/2, metrics_mit, width, label='Mit class_weight="balanced"', color='lightgreen')
# Beschriftungen, Titel und benutzerdefinierte x-Achsen-Tick-Labels usw.
ax.set_ylabel('Score')
ax.set_title('Metriken für Minderheitsklasse (Klasse 1)')
ax.set_xticks(x)
ax.set_xticklabels(metric_names)
ax.legend()
ax.set_ylim(0, 1.1) # Y-Achse bis knapp über 1.0 für bessere Sichtbarkeit
def autolabel(rects):
"""Fügt Labels über den Balken hinzu."""
for rect in rects:
height = rect.get_height()
ax.annotate(f'{height:.2f}',
xy=(rect.get_x() + rect.get_width() / 2, height),
xytext=(0, 3), # 3 points vertical offset
textcoords="offset points",
ha='center', va='bottom')
autolabel(rects1)
autolabel(rects2)
fig.tight_layout()
plt.show()Ausgabe:
Verteilung der Klassen im gesamten Datensatz: Counter({np.int64(0): 9285, np.int64(1): 715})
Verteilung der Klassen im Trainingsdatensatz: Counter({np.int64(0): 6500, np.int64(1): 500})
Verteilung der Klassen im Testdatensatz: Counter({np.int64(0): 2785, np.int64(1): 215})
--------------------------------------------------
Classification Report (OHNE class_weight):
precision recall f1-score support
Klasse 0 (Mehrheit) 0.94 1.00 0.97 2785
Klasse 1 (Minderheit) 0.96 0.24 0.39 215
accuracy 0.94 3000
macro avg 0.95 0.62 0.68 3000
weighted avg 0.95 0.94 0.93 3000
ROC AUC Score (OHNE class_weight): 0.7754
--------------------------------------------------
Classification Report (MIT class_weight='balanced'):
precision recall f1-score support
Klasse 0 (Mehrheit) 0.97 0.76 0.85 2785
Klasse 1 (Minderheit) 0.18 0.68 0.28 215
accuracy 0.75 3000
macro avg 0.57 0.72 0.57 3000
weighted avg 0.91 0.75 0.81 3000
ROC AUC Score (MIT class_weight='balanced'): 0.7829
--------------------------------------------------
Die Ergebnisse demonstrieren den Effekt der class_weight-Anpassung. Im gesamten Datensatz sind 9285 Instanzen der Klasse 0 (Mehrheit) und nur 715 der Klasse 1 (Minderheit) vorhanden. Diese Verteilung spiegelt sich dann auch in den Trainingsdaten und den Testdaten wider.
Beim Training des Modells ohne spezifische Gewichtung (class_weight) erzielt das System eine hohe Gesamtgenauigkeit von 0.94. Dies ist jedoch primär auf die exzellente Erkennung der Mehrheitsklasse (Klasse 0) zurückzuführen, die einen Recall von 1.00 bei einer Precision von 0.94 und einem F1-Score von 0.97 erreicht. Die Minderheitsklasse (Klasse 1) wird hingegen sehr schlecht erkannt: Obwohl die Precision mit 0.96 relativ hoch ist, wenn sie denn einmal korrekt vorhergesagt wird, beträgt der Recall lediglich 0.24. Das bedeutet, nur 24% der tatsächlichen Minderheitsinstanzen werden korrekt identifiziert, was zu einem F1-Score von nur 0.39 für diese Klasse führt. Der ROC AUC Score liegt für dieses Modell bei 0.7754.
Durch die Aktivierung von class_weight=’balanced‘ verschiebt sich das Verhalten des Modells deutlich, um die Minderheitsklasse besser zu berücksichtigen. Die Gesamtgenauigkeit sinkt auf 0.75. Für die Mehrheitsklasse (Klasse 0) reduziert sich der Recall auf 0.76, während die Precision bei 0.97 verbleibt, was einen F1-Score von 0.85 ergibt. Entscheidend ist die Veränderung bei der Minderheitsklasse (Klasse 1): Der Recall steigt hier markant auf 0.68 an, was bedeutet, dass nun 68% der seltenen Instanzen korrekt erkannt werden. Dieser signifikante Gewinn im Recall geht allerdings mit einer deutlichen Reduktion der Precision auf 0.18 für diese Klasse einher. Das heißt, wenn das Modell Klasse 1 vorhersagt, ist es seltener korrekt als zuvor. Dies führt zu einem F1-Score von 0.28 für die Minderheitsklasse. Der ROC AUC Score verbessert sich leicht auf 0.7829, was auf eine marginal bessere generelle Trennfähigkeit der Klassen hindeutet.
Die Verwendung von class_weight=’balanced‘ verschiebt den Fokus des Modells auf die Erkennung der unterrepräsentierten Klasse, was sich in einem stark erhöhten Recall für die Minderheitsklasse zeigt. Dieser Gewinn wird jedoch mit einer reduzierten Performance bei der Mehrheitsklasse und einer geringeren Precision für die Minderheitsklasse erkauft.

Die linke Confusion-Matrix zeigt, dass das Modell ohne Klassen-Gewichtung 2783 Instanzen der Mehrheitsklasse (Klasse 0) korrekt als Klasse 0 klassifiziert hat. Nur 2 Instanzen der Mehrheitsklasse wurden fälschlicherweise als Minderheitsklasse (Klasse 1) vorhergesagt. Bei der Minderheitsklasse (Klasse 1) wurden jedoch nur 52 Instanzen korrekt als Klasse 1 identifiziert, während 163 Instanzen der Minderheitsklasse fälschlicherweise als Mehrheitsklasse klassifiziert wurden. Dies verdeutlicht, dass das Modell stark zur Mehrheitsklasse tendiert und die Minderheitsklasse größtenteils übersieht.
Die rechte Confusion Matrix zeigt ein deutlich verändertes Bild. Die Anzahl der korrekt als Mehrheitsklasse (Klasse 0) klassifizierten Instanzen ist auf 2115 gesunken. Gleichzeitig wurden nun 670 Instanzen der Mehrheitsklasse fälschlicherweise als Minderheitsklasse (Klasse 1) vorhergesagt, was einen deutlichen Anstieg der False Positives für die Minderheitsklasse bedeutet. Entscheidend ist die Verbesserung bei der Minderheitsklasse (Klasse 1): Die Anzahl der korrekt als Klasse 1 identifizierten Instanzen ist auf 146 gestiegen. Im Gegenzug ist die Anzahl der fälschlicherweise als Mehrheitsklasse klassifizierten Minderheitsinstanzen (False Negatives) auf 69 gesunken.
Zusammenfassend zeigen die Matrizen, dass die Verwendung von class_weight=“balanced“ dazu geführt hat, dass das Modell die Minderheitsklasse signifikant besser erkennt. Dieser Gewinn bei der Erkennung der Minderheitsklasse geht jedoch mit einer Zunahme von Fehlklassifikationen bei der Mehrheitsklasse einher, insbesondere werden mehr Instanzen der Mehrheitsklasse fälschlicherweise der Minderheitsklasse zugeordnet.
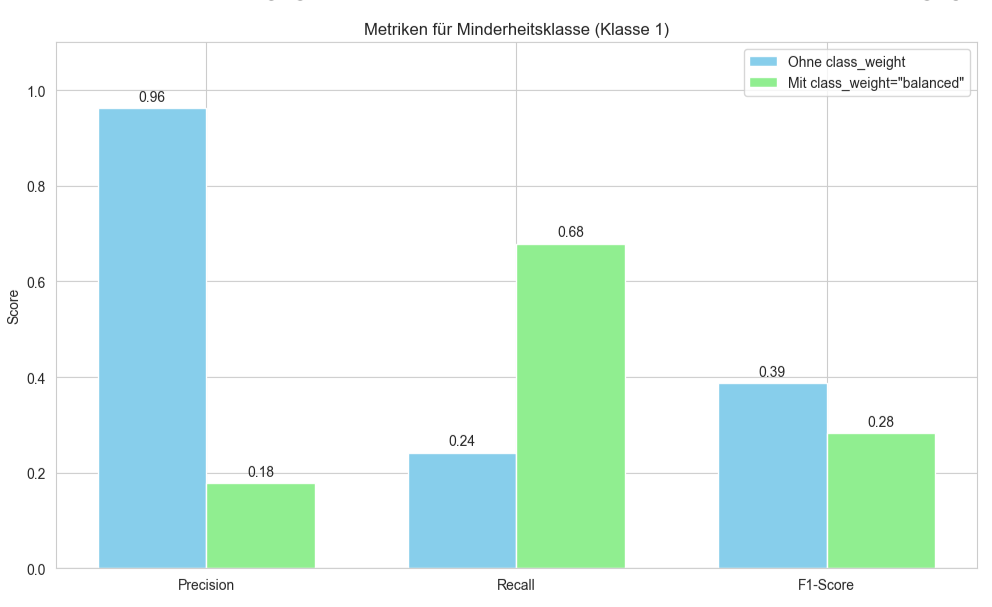
Das Balkendiagramm vergleicht die Leistungskennzahlen Precision, Recall und F1-Score speziell für die Minderheitsklasse eines Klassifikationsmodells. Für jede dieser drei Metriken werden zwei Balken nebeneinander dargestellt: ein Balken für das Modell „Ohne class_weight“ und ein Balken für das Modell „Mit class_weight=’balanced'“. Die y-Achse zeigt den „Score“ der jeweiligen Metrik, der von 0.0 bis ca. 1.0 reicht.
Beim Betrachten der „Precision“ zeigt der hellblaue Balken („Ohne class_weight“) einen sehr hohen Wert von 0.96, während der hellgrüne Balken („Mit class_weight=’balanced'“) einen deutlich niedrigeren Wert von 0.18 aufweist. Dies deutet darauf hin, dass das Modell ohne Gewichtung, wenn es die Minderheitsklasse vorhersagt, dies mit hoher Präzision tut, während das Modell mit Gewichtung bei seinen Vorhersagen für die Minderheitsklasse öfter falsch liegt.
Im Gegensatz dazu steht der „Recall“. Hier ist der hellblaue Balken („Ohne class_weight“) mit einem Wert von 0.24 sehr niedrig, was bedeutet, dass nur ein kleiner Teil der tatsächlichen Minderheitsklassen-Instanzen erkannt wird. Der hellgrüne Balken („Mit class_weight=’balanced'“) hingegen erreicht einen signifikant höheren Wert von 0.68. Dies illustriert, dass die Verwendung von class_weight die Fähigkeit des Modells, tatsächliche Instanzen der Minderheitsklasse zu identifizieren, erheblich verbessert hat.
Schließlich zeigt der „F1-Score“, der das harmonische Mittel aus Precision und Recall darstellt, für das Modell „Ohne class_weight“ (hellblauer Balken) einen Wert von 0.39. Für das Modell „Mit class_weight=’balanced'“ (hellgrüner Balken) ist der F1-Score mit 0.28 niedriger. Dies legt nahe, dass der starke Abfall der Precision bei Verwendung von class_weight den deutlichen Anstieg des Recalls in der kombinierten F1-Metrik für die Minderheitsklasse in diesem spezifischen Fall überkompensiert hat.
Zusammenfassend visualisiert das Diagramm den Kompromiss, der durch die Verwendung von class_weight=’balanced‘ entsteht: eine drastische Verbesserung des Recalls für die Minderheitsklasse auf Kosten einer erheblichen Reduktion der Precision für dieselbe Klasse, was sich hier auch in einem niedrigeren F1-Score niederschlägt.
SMOTE mit externen Bibliotheken
SMOTE steht für Synthetic Minority Over-sampling TEchnique. Es ist eine Methode, um das Problem von unbalancierten Klassen anzugehen. Die Grundidee von SMOTE ist es, die Minderheitsklasse nicht einfach zu Duplizieren (was zu Overfitting führen kann), sondern synthetische (künstliche) neue Instanzen zu generieren, die den vorhandenen Instanzen der Minderheitsklasse ähneln. Dazu wählt SMOTE zufällig eine Instanz aus der Minderheitsklasse aus. Für diese ausgewählte Instanz werden ihre k nächsten Nachbarn (k-nearest neighbors, KNN) identifiziert, die ebenfalls zur Minderheitsklasse gehören. Die Anzahl k ist ein Parameter, der typischerweise auf 5 gesetzt wird. Einer dieser Nachbarn wird zufällig ausgewählt und ein neuer, synthetischer Datenpunkt wird entlang einer Linie erzeugt, die die ursprüngliche Instanz und den ausgewählten Nachbarn im Merkmalsraum verbindet. Die Position dieses neuen Punktes wird zufällig entlang dieser Linie gewählt. Dieser Vorgang wird so oft wiederholt, bis die gewünschte Anzahl synthetischer Instanzen für die Minderheitsklasse erzeugt wurde, um das Klassengleichgewicht zu verbessern. Im Gegensatz zum einfachen Duplizieren von Minderheitsinstanzen, erzeugt SMOTE neue Datenpunkte. Dies hilft dem Modell, die Entscheidungsregion für die Minderheitsklasse besser zu erlernen und zu verallgemeinern.
Oft führt SMOTE zu einer besseren Leistung des Klassifikators für die Minderheitsklasse, gemessen an Metriken wie Recall, F1-Score oder AUC, da das Modell mehr „Beispiele“ zum Lernen hat.
SMOTE darf nur auf die Trainingsdaten angewendet werden, niemals auf die Testdaten. Die Testdaten müssen die ursprüngliche, reale Verteilung der Klassen widerspiegeln, um eine unverfälschte Bewertung der Modellleistung zu ermöglichen.
Wenn die Minderheitsklasse sehr spärlich ist oder ihre Instanzen nahe an der Grenze zur Mehrheitsklasse liegen, kann es passieren, dass SMOTE synthetische Instanzen erzeugt, die in die Region der Mehrheitsklasse „hineinragen“ oder die Klassengrenzen verschwimmen lassen. Dies kann die Klassifikation erschweren. SMOTE berücksichtigt nicht, ob die Nachbarn selbst Ausreißer oder verrauschte Daten sind. Wenn eine Minderheitsinstanz ein Ausreißer ist, kann SMOTE weitere synthetische Ausreißer um sie herum erzeugen. Aufgrund dieser Nachteile gibt es viele Varianten von SMOTE, wie z.B.:
- Borderline-SMOTE: Konzentriert sich auf die Generierung von Instanzen nahe der Klassengrenze.
- ADASYN (Adaptive Synthetic Sampling): Generiert mehr synthetische Daten für Minderheitsklassen-Instanzen, die schwieriger zu lernen sind (d.h. mehr Nachbarn aus der Mehrheitsklasse haben).
Für das folgende Beispiel muss die Python Bibliothek imbalanced-learn mit folgendem Befehl installiert werden:
!pip install -U imbalanced-learnDas folgende Beispiel generiert zunächst wieder den synthetischen, binären Klassifikationsdatensatz mit einem starken Klassenungleichgewicht und teilt diesen anschließend in Trainings- und Testmengen auf, wobei die Klassenproportionen in beiden Mengen erhalten bleiben. Daraufhin wird ein erstes Logistisches Regressionsmodell auf den originalen, unbalancierten Trainingsdaten trainiert, und seine Leistung wird anhand von Vorhersagen und Wahrscheinlichkeiten auf den Testdaten bewertet, wobei Metriken wie der Classification Report, die Confusion Matrix und der ROC AUC Score berechnet werden. Anschließend wird die SMOTE-Technik (Synthetic Minority Over-sampling Technique) angewendet, um die Anzahl der Samples zu der Minderheitsklasse im Trainingsdatensatz durch die Generierung synthetischer Samples auszugleichen, wodurch ein neuer, balancierter Trainingsdatensatz entsteht. Ein zweites, identisch konfiguriertes Logistisches Regressionsmodell wird dann auf diesem mit SMOTE behandelten, balancierten Trainingsdatensatz trainiert. Die Leistung dieses zweiten Modells wird ebenfalls auf den ursprünglichen, Testdaten evaluiert, indem erneut Vorhersagen und Wahrscheinlichkeiten generiert und die entsprechenden Metriken berechnet werden, um die Auswirkungen von SMOTE auf die Modellgüte zu vergleichen.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import (
classification_report,
confusion_matrix,
roc_auc_score,
roc_curve
)
from collections import Counter
from imblearn.over_sampling import SMOTE # Wichtig: SMOTE importieren
# Erstellen des unbalancierten Datensatzes
X, y = make_classification(n_samples=10000, n_features=20, n_informative=15,
n_redundant=5, n_classes=2, weights=[0.95, 0.05],
flip_y=0.05, random_state=42)
print(f"Verteilung der Klassen im gesamten Datensatz: {Counter(y)}")
# Aufteilen in Trainings- und Testdaten
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
print(f"Verteilung der Klassen im Trainingsdatensatz VOR SMOTE: {Counter(y_train)}")
print(f"Verteilung der Klassen im Testdatensatz: {Counter(y_test)}")
print("-" * 50)
# Modelltraining OHNE SMOTE
print("Modelltraining OHNE SMOTE (Baseline):")
model_ohne_smote = LogisticRegression(solver='liblinear', random_state=42)
model_ohne_smote.fit(X_train, y_train) # Training auf originalen Trainingsdaten
y_pred_ohne_smote = model_ohne_smote.predict(X_test)
y_proba_ohne_smote = model_ohne_smote.predict_proba(X_test)[:, 1]
print("\nClassification Report (OHNE SMOTE):")
report_ohne_smote = classification_report(y_test, y_pred_ohne_smote, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)'], output_dict=True)
print(classification_report(y_test, y_pred_ohne_smote, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)']))
cm_ohne_smote = confusion_matrix(y_test, y_pred_ohne_smote)
auc_ohne_smote = roc_auc_score(y_test, y_proba_ohne_smote)
print(f"ROC AUC Score (OHNE SMOTE): {auc_ohne_smote:.4f}")
print("-" * 50)
# Anwenden von SMOTE auf die Trainingsdaten und Modelltraining
print("Anwenden von SMOTE auf die Trainingsdaten...")
smote = SMOTE(random_state=42) # Standardmäßig wird die Minderheitsklasse auf die Größe der Mehrheitsklasse überabgetastet
X_train_smote, y_train_smote = smote.fit_resample(X_train, y_train)
print(f"Verteilung der Klassen im Trainingsdatensatz NACH SMOTE: {Counter(y_train_smote)}")
print("-" * 50)
print("Modelltraining MIT SMOTE:")
model_mit_smote = LogisticRegression(solver='liblinear', random_state=42)
model_mit_smote.fit(X_train_smote, y_train_smote) # Training auf den mit SMOTE überabgetasteten Trainingsdaten
y_pred_mit_smote = model_mit_smote.predict(X_test) # Vorhersage auf den *originalen* Testdaten
y_proba_mit_smote = model_mit_smote.predict_proba(X_test)[:, 1]
print("\nClassification Report (MIT SMOTE):")
report_mit_smote = classification_report(y_test, y_pred_mit_smote, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)'], output_dict=True)
print(classification_report(y_test, y_pred_mit_smote, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)']))
cm_mit_smote = confusion_matrix(y_test, y_pred_mit_smote)
auc_mit_smote = roc_auc_score(y_test, y_proba_mit_smote)
print(f"ROC AUC Score (MIT SMOTE): {auc_mit_smote:.4f}")
print("-" * 50)
# Visualisierungen
target_names = ['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)']
# Confusion Matrices
fig, axes = plt.subplots(1, 2, figsize=(14, 5))
sns.heatmap(cm_ohne_smote, annot=True, fmt='d', cmap='Blues', ax=axes[0],
xticklabels=target_names, yticklabels=target_names)
axes[0].set_title('Confusion Matrix (Ohne SMOTE)')
axes[0].set_xlabel('Vorhergesagte Klasse')
axes[0].set_ylabel('Tatsächliche Klasse')
sns.heatmap(cm_mit_smote, annot=True, fmt='d', cmap='Greens', ax=axes[1],
xticklabels=target_names, yticklabels=target_names)
axes[1].set_title('Confusion Matrix (Mit SMOTE auf Trainingsdaten)')
axes[1].set_xlabel('Vorhergesagte Klasse')
axes[1].set_ylabel('Tatsächliche Klasse')
plt.tight_layout()
plt.show()
# Balkendiagramm für Metriken der Minderheitsklasse
metrics_ohne = [
report_ohne_smote['Klasse 1 (Minderheit)']['precision'],
report_ohne_smote['Klasse 1 (Minderheit)']['recall'],
report_ohne_smote['Klasse 1 (Minderheit)']['f1-score']
]
metrics_mit = [
report_mit_smote['Klasse 1 (Minderheit)']['precision'],
report_mit_smote['Klasse 1 (Minderheit)']['recall'],
report_mit_smote['Klasse 1 (Minderheit)']['f1-score']
]
metric_names = ['Precision', 'Recall', 'F1-Score']
x = np.arange(len(metric_names))
width = 0.35
fig, ax = plt.subplots(figsize=(10, 6))
rects1 = ax.bar(x - width/2, metrics_ohne, width, label='Ohne SMOTE', color='skyblue')
rects2 = ax.bar(x + width/2, metrics_mit, width, label='Mit SMOTE', color='lightgreen')
ax.set_ylabel('Score')
ax.set_title('Metriken für Minderheitsklasse (Klasse 1)')
ax.set_xticks(x)
ax.set_xticklabels(metric_names)
ax.legend()
ax.set_ylim(0, 1.1)
def autolabel(rects):
for rect in rects:
height = rect.get_height()
ax.annotate(f'{height:.2f}',
xy=(rect.get_x() + rect.get_width() / 2, height),
xytext=(0, 3),
textcoords="offset points",
ha='center', va='bottom')
autolabel(rects1)
autolabel(rects2)
fig.tight_layout()
plt.show()Ausgaben:
Verteilung der Klassen im gesamten Datensatz: Counter({np.int64(0): 9285, np.int64(1): 715})
Verteilung der Klassen im Trainingsdatensatz VOR SMOTE: Counter({np.int64(0): 6500, np.int64(1): 500})
Verteilung der Klassen im Testdatensatz: Counter({np.int64(0): 2785, np.int64(1): 215})
--------------------------------------------------
Modelltraining OHNE SMOTE (Baseline):
Classification Report (OHNE SMOTE):
precision recall f1-score support
Klasse 0 (Mehrheit) 0.94 1.00 0.97 2785
Klasse 1 (Minderheit) 0.96 0.24 0.39 215
accuracy 0.94 3000
macro avg 0.95 0.62 0.68 3000
weighted avg 0.95 0.94 0.93 3000
ROC AUC Score (OHNE SMOTE): 0.7754
--------------------------------------------------
Anwenden von SMOTE auf die Trainingsdaten...
Verteilung der Klassen im Trainingsdatensatz NACH SMOTE: Counter({np.int64(0): 6500, np.int64(1): 6500})
--------------------------------------------------
Modelltraining MIT SMOTE:
Classification Report (MIT SMOTE):
precision recall f1-score support
Klasse 0 (Mehrheit) 0.97 0.77 0.86 2785
Klasse 1 (Minderheit) 0.18 0.66 0.28 215
accuracy 0.76 3000
macro avg 0.57 0.71 0.57 3000
weighted avg 0.91 0.76 0.81 3000
ROC AUC Score (MIT SMOTE): 0.7805
--------------------------------------------------
Die Ergebnisses des Beispiels zeigen deutlich die Auswirkungen der Minderheitsklasse auf die Modellleistung.
Ausgangssituation (Ohne SMOTE):
Der Datensatz ist stark unbalanciert, mit 9285 Instanzen der Mehrheitsklasse (0) und nur 715 der Minderheitsklasse (1) insgesamt. Dies spiegelt sich im Trainingsdatensatz wider (6500 vs. 500). Das Baseline-Modell, das ohne SMOTE auf diesen unbalancierten Daten trainiert wurde, erzielt eine hohe Gesamtgenauigkeit von 0.94. Dies ist jedoch trügerisch, da es primär auf der fast perfekten Erkennung der Mehrheitsklasse beruht (Recall 1.00, Precision 0.94). Die kritische Minderheitsklasse wird hingegen sehr schlecht erkannt: Obwohl die Precision mit 0.96 gut ist, ist der Recall mit 0.24 extrem niedrig. Das bedeutet, nur 24% der Minderheitsinstanzen werden korrekt identifiziert, was zu einem schlechten F1-Score von 0.39 für diese Klasse führt.
SMOTE wurde angewendet, um den Trainingsdatensatz auszubalancieren, sodass nun jeweils 6500 Instanzen für Klasse 0 und Klasse 1 im Trainingsset vorhanden sind. Das Modell, das auf diesen mit SMOTE multiplizierten Daten trainiert wurde, zeigt folgende Veränderungen in der Leistung auf dem unveränderten Testdatensatz:
- Klasse 1
Der Recall ist signifikant von 0.24 auf 0.66 gestiegen. Das Modell erkennt nun einen deutlich größeren Anteil der tatsächlichen Minderheitsinstanzen.
Die Precision ist jedoch drastisch von 0.96 auf 0.18 gesunken. Das bedeutet, dass viele Vorhersagen der Klasse 1 nun falsch positiv sind. - Klasse 0
Der Recall ist von 1.00 auf 0.77 gesunken, während die Precision leicht von 0.94 auf 0.97 gestiegen ist. Der F1-Score ist von 0.97 auf 0.86 gefallen. - Gesamtmetriken:
Die Gesamtgenauigkeit ist von 0.94 auf 0.76 gesunken, was zu erwarten ist, da das Modell nicht mehr primär die Mehrheitsklasse favorisiert.
Der ROC AUC Score hat sich leicht von 0.7754 auf 0.7805 verbessert, was auf eine marginal bessere generelle Fähigkeit des Modells hindeutet, die Klassen zu trennen.
SMOTE hat sein primäres Ziel erreicht. Die Erkennungsrate der Minderheitsklasse signifikant zu verbessern. Das Modell ist nun viel sensibler für die seltene Klasse. Allerdings auf Kosten einer stark reduzierten Gesamtgenauigkeit.

Die Confusion-Matritzen sind vergleichbar mit den Ergebnissen zu dem Beispiel class_weight=“balanced“. Die Werte weichen nur minimal ab.

Die Das Balkendiagramm ist auch vergleichbar mit den Ergebnissen aus dem Beispiel class_weight=“balanced“. Was darauf hindeutet, dass bei Methoden vergleichbare Ergebnisse erzielen.
Vergleich class_weight mit SMOTE
Beim Vergleich der Ergebnisse von class_weight=’balanced‘ und SMOTE fällt auf, dass beide Ansätze zu ähnlichen Resultaten in der Klassifikationsleistung führen, insbesondere hinsichtlich der kritischen Minderheitsklasse. Für die Minderheitsklasse (Klasse 1) erzielen sowohl class_weight als auch SMOTE eine identische Precision von 0.18 und einen identischen F1-Score von 0.28. Der Recall für die Minderheitsklasse ist ebenfalls sehr vergleichbar, wobei class_weight mit 0.68 einen minimal höheren Wert erreicht als SMOTE mit 0.66. Beide Methoden haben also den Recall im Vergleich zum Baseline-Modell (das einen Recall von 0.24 hatte) erheblich gesteigert, dies jedoch auf Kosten einer deutlich reduzierten Precision.
Auch bei der Betrachtung der Mehrheitsklasse (Klasse 0) sind die Unterschiede gering: Die Precision ist bei beiden Methoden 0.97. SMOTE erzielt einen marginal besseren Recall (0.77 gegenüber 0.76 für class_weight) und F1-Score (0.86 gegenüber 0.85 für class_weight). Die Gesamtgenauigkeit ist mit 0.75 für class_weight und 0.76 für SMOTE fast gleich. Interessanterweise zeigt der ROC AUC Score für class_weight=’balanced‘ mit 0.7829 einen geringfügig besseren Wert als für SMOTE mit 0.7805, was auf eine minimal überlegene generelle Trennfähigkeit der Klassen durch die Gewichtungsmethode hindeutet.
