TODO für Tag 27
- ROC-Kurve plotten und AUC berechnen (roc_auc_score)
ROC-Kurve plotten und AUC berechnen (roc_auc_score)
Die ROC Kurve (Receiver Operating Characteristic Kurve), ist ein grafisches Werkzeug, das die Leistungsfähigkeit eines binären Klassifikationsmodells über verschiedene Schwellenwerte hinweg visualisiert. Auf der y Achse wird die Sensitivität oder Trefferquote abgetragen, während die x Achse die False-Positiv-Rate darstellt. Eine Diagonale von links unten nach rechts oben repräsentiert die Leistung eines Zufallsklassifikators. Die Fläche unter dieser Kurve, bekannt als AUC (Area Under the Curve), dient als zusammenfassendes Maß für die Modellgüte über alle Schwellenwerte hinweg; ein höherer AUC Wert, idealerweise nahe 1, deutet auf eine bessere Unterscheidungsfähigkeit des Modells hin.
Um eine solche Kurve mit der Python Bibliothek scikit learn zu erstellen, benötigt man zunächst die wahren Zielwerte und die vom Modell vorhergesagten Wahrscheinlichkeiten für die positive Klasse. Die Funktion roc_curve aus dem Modul sklearn.metrics ist hierfür zentral. Man übergibt ihr die wahren Labels, typischerweise als y_true bezeichnet, und die vorhergesagten Wahrscheinlichkeiten der positiven Klasse, oft y_scores genannt. Diese Funktion liefert drei Arrays zurück: die Falsch-Positiv-Raten, die Richtig-Positiv-Raten und die entsprechenden Schwellenwerte, die zu diesen Raten geführt haben. Diese Raten können dann beispielsweise mit matplotlib.pyplot geplottet werden, indem die Falsch-Positiv-Raten auf der x Achse und die Richtig-Positiv-Raten auf der y Achse dargestellt werden.
Zusätzlich lässt sich der AUC Wert direkt mit der Funktion roc_auc_score (sklearn.metrics) berechnen, indem man ihr wiederum die wahren Labels und die Wahrscheinlichkeitsprognosen übergibt. Man importiert also roc_curve und roc_auc_score. Nach dem Training eines Klassifikators und der Vorhersage von Wahrscheinlichkeiten für die positive Klasseruft man roc_curve auf. Anschließend kann das Ergebnis verwendet werden, um die Kurve zu zeichnen.
Das Folgende Beispiel entspricht dem Beispiel von Tag 26, dass statt der Confusion-Matrix und dem Balkendiagram die ROC-Kurve zeichnet.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import (
classification_report,
confusion_matrix,
roc_auc_score,
roc_curve # roc_curve ist bereits importiert, aber zur Verdeutlichung hier nochmals erwähnt
)
from collections import Counter
from imblearn.over_sampling import SMOTE # Wichtig: SMOTE importieren
# Erstellen des unbalancierten Datensatzes
X, y = make_classification(n_samples=10000, n_features=20, n_informative=15,
n_redundant=5, n_classes=2, weights=[0.95, 0.05],
flip_y=0.05, random_state=42)
print(f"Verteilung der Klassen im gesamten Datensatz: {Counter(y)}")
# Aufteilen in Trainings- und Testdaten
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
print(f"Verteilung der Klassen im Trainingsdatensatz VOR SMOTE: {Counter(y_train)}")
print(f"Verteilung der Klassen im Testdatensatz: {Counter(y_test)}")
print("-" * 50)
# Modelltraining OHNE SMOTE
print("Modelltraining OHNE SMOTE (Baseline):")
model_ohne_smote = LogisticRegression(solver='liblinear', random_state=42)
model_ohne_smote.fit(X_train, y_train) # Training auf originalen Trainingsdaten
y_pred_ohne_smote = model_ohne_smote.predict(X_test)
y_proba_ohne_smote = model_ohne_smote.predict_proba(X_test)[:, 1] # Wahrscheinlichkeiten für die positive Klasse
print("\nClassification Report (OHNE SMOTE):")
report_ohne_smote = classification_report(y_test, y_pred_ohne_smote, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)'], output_dict=True)
print(classification_report(y_test, y_pred_ohne_smote, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)']))
cm_ohne_smote = confusion_matrix(y_test, y_pred_ohne_smote)
auc_ohne_smote = roc_auc_score(y_test, y_proba_ohne_smote)
print(f"ROC AUC Score (OHNE SMOTE): {auc_ohne_smote:.4f}")
print("-" * 50)
# Anwenden von SMOTE auf die Trainingsdaten und Modelltraining
print("Anwenden von SMOTE auf die Trainingsdaten...")
smote = SMOTE(random_state=42) # Standardmäßig wird die Minderheitsklasse auf die Größe der Mehrheitsklasse überabgetastet
X_train_smote, y_train_smote = smote.fit_resample(X_train, y_train)
print(f"Verteilung der Klassen im Trainingsdatensatz NACH SMOTE: {Counter(y_train_smote)}")
print("-" * 50)
print("Modelltraining MIT SMOTE:")
model_mit_smote = LogisticRegression(solver='liblinear', random_state=42)
model_mit_smote.fit(X_train_smote, y_train_smote) # Training auf den mit SMOTE überabgetasteten Trainingsdaten
y_pred_mit_smote = model_mit_smote.predict(X_test) # Vorhersage auf den *originalen* Testdaten
y_proba_mit_smote = model_mit_smote.predict_proba(X_test)[:, 1] # Wahrscheinlichkeiten für die positive Klasse
print("\nClassification Report (MIT SMOTE):")
report_mit_smote = classification_report(y_test, y_pred_mit_smote, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)'], output_dict=True)
print(classification_report(y_test, y_pred_mit_smote, target_names=['Klasse 0 (Mehrheit)', 'Klasse 1 (Minderheit)']))
cm_mit_smote = confusion_matrix(y_test, y_pred_mit_smote)
auc_mit_smote = roc_auc_score(y_test, y_proba_mit_smote)
print(f"ROC AUC Score (MIT SMOTE): {auc_mit_smote:.4f}")
print("-" * 50)
# Berechnung der ROC-Kurven-Daten für das Modell OHNE SMOTE
fpr_ohne_smote, tpr_ohne_smote, thresholds_ohne_smote = roc_curve(y_test, y_proba_ohne_smote)
# Berechnung der ROC-Kurven-Daten für das Modell MIT SMOTE
fpr_mit_smote, tpr_mit_smote, thresholds_mit_smote = roc_curve(y_test, y_proba_mit_smote)
# Erstellung des ROC-Kurven-Diagramms
plt.figure(figsize=(10, 7)) # Festlegen der Größe der Abbildung
# Plotten der ROC-Kurve für das Modell OHNE SMOTE
plt.plot(fpr_ohne_smote, tpr_ohne_smote, label=f'Modell OHNE SMOTE (AUC = {auc_ohne_smote:.4f})')
# Plotten der ROC-Kurve für das Modell MIT SMOTE
plt.plot(fpr_mit_smote, tpr_mit_smote, label=f'Modell MIT SMOTE (AUC = {auc_mit_smote:.4f})')
# Plotten der Referenzlinie für einen Zufallsklassifikator
plt.plot([0, 1], [0, 1], linestyle='--', color='grey', label='Zufallsklassifikator (AUC = 0.5000)')
# Hinzufügen von Titel und Achsenbeschriftungen
plt.title('Vergleich der ROC-Kurven: Mit und ohne SMOTE')
plt.xlabel('Falsch-Positiv-Rate (1 - Spezifität)')
plt.ylabel('Richtig-Positiv-Rate (Sensitivität/Recall)')
plt.legend(loc='lower right') # Positionierung der Legende
plt.grid(True) # Hinzufügen eines Gitters zur besseren Lesbarkeit
plt.show() # Anzeigen des DiagrammsAusgabe:
Verteilung der Klassen im gesamten Datensatz: Counter({np.int64(0): 9285, np.int64(1): 715})
Verteilung der Klassen im Trainingsdatensatz VOR SMOTE: Counter({np.int64(0): 6500, np.int64(1): 500})
Verteilung der Klassen im Testdatensatz: Counter({np.int64(0): 2785, np.int64(1): 215})
--------------------------------------------------
Modelltraining OHNE SMOTE (Baseline):
Classification Report (OHNE SMOTE):
precision recall f1-score support
Klasse 0 (Mehrheit) 0.94 1.00 0.97 2785
Klasse 1 (Minderheit) 0.96 0.24 0.39 215
accuracy 0.94 3000
macro avg 0.95 0.62 0.68 3000
weighted avg 0.95 0.94 0.93 3000
ROC AUC Score (OHNE SMOTE): 0.7754
--------------------------------------------------
Anwenden von SMOTE auf die Trainingsdaten...
Verteilung der Klassen im Trainingsdatensatz NACH SMOTE: Counter({np.int64(0): 6500, np.int64(1): 6500})
--------------------------------------------------
Modelltraining MIT SMOTE:
Classification Report (MIT SMOTE):
precision recall f1-score support
Klasse 0 (Mehrheit) 0.97 0.77 0.86 2785
Klasse 1 (Minderheit) 0.18 0.66 0.28 215
accuracy 0.76 3000
macro avg 0.57 0.71 0.57 3000
weighted avg 0.91 0.76 0.81 3000
ROC AUC Score (MIT SMOTE): 0.7805
--------------------------------------------------
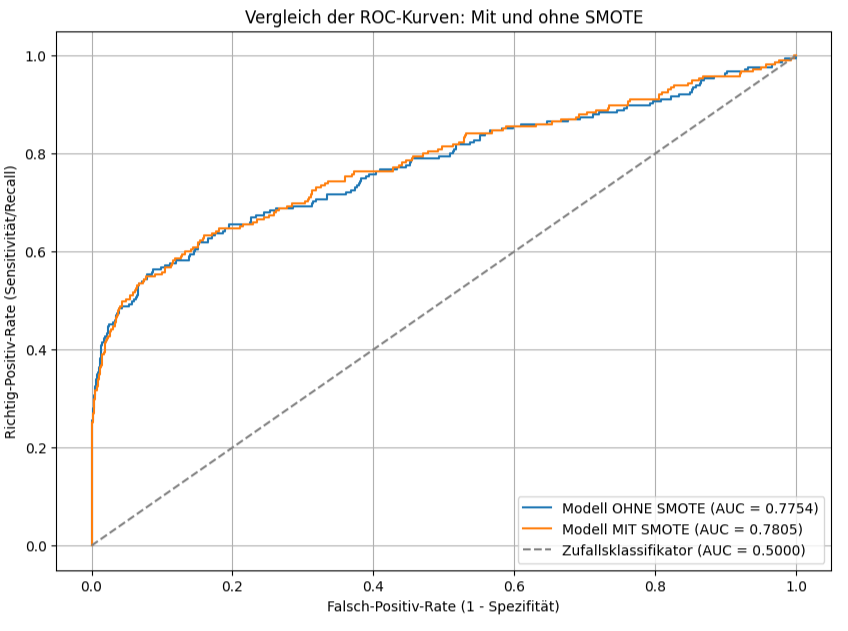
Die ROC-Kurve visualisiert die Leistung der beiden Klassifikationsmodelle, ohne SMOTE und mit SMOTE. Zusätzlich ist die Diagonale als Referenz für einen Zufallsklassifikator eingezeichnet. Die x Achse zeigt die Falsch-Positiv-Rate, also den Anteil der tatsächlich negativen Fälle, die fälschlicherweise als positiv klassifiziert wurden. Die y Achse stellt die Richtig-Positiv-Rate dar, also den Anteil der tatsächlich positiven Fälle, die korrekt als positiv erkannt wurden.
Sowohl die blaue Kurve (OHNE SMOTE) als auch die orange Kurve (MIT SMOTE) liegen deutlich oberhalb der gestrichelten diagonalen Linie des Zufallsklassifikators. Dies bedeutet, dass beide Modelle eine bessere Unterscheidungsfähigkeit als reines Raten besitzen. Das „Modell OHNE SMOTE“ erreicht einen AUC-Wert von 0.7754. Das „Modell MIT SMOTE“ erreicht einen AUC-Wert von 0.7805. Der AUC-Wert (Area Under Curve) ist ein Maß für die Gesamtperformanz des Modells über alle möglichen Schwellenwerte hinweg. Ein höherer AUC-Wert deutet auf eine bessere Fähigkeit des Modells hin, zwischen den positiven und negativen Klassen zu unterscheiden.
Das Modell, das auf „SMOTE“ Trainingsdaten trainiert wurde, weist einen geringfügig höheren AUC-Wert auf. Das bedeutet, die Anwendung von SMOTE liefert in diesem spezifischen Fall ein minimal besseres Modell. Die orange Kurve verläuft über weite Strecken leicht oberhalb oder deckungsgleich mit der blauen Kurve. Das bedeutet, dass für die meisten Falsch-Positiv-Raten das Modell mit SMOTE eine gleich hohe oder leicht höhere Richtig-Positiv-Rate erzielt.
Die Anwendung von SMOTE hat die Unterscheidungsfähigkeit des Modells, gemessen am AUC, leicht verbessert. Der Unterschied in der AUC ist aber sehr gering, was darauf hindeutet, dass der Effekt von SMOTE auf die Performance in diesem speziellen Szenario eher überschaubar ist.
