TODO für Tag 29
- Einführung in Multi-Output Methoden
Einführung in Multi-Output Methoden
Beim Maschine Learning ist es oft die Aufgaben, eine einzelne Zielvariable vorherzusagen. Es gibt jedoch Szenarien, in denen es notwendig ist, mehrere Zielvariablen gleichzeitig aus denselben Eingabemerkmalen zu prognostizieren. Diese Art von Problemstellung wird als Multi-Output-Vorhersage bezeichnet und kann sowohl Regressions- als auch Klassifikationsaufgaben umfassen. Anstatt für jede Multi-Output-Aufgabe völlig neue Algorithmen zu implementieren, verfolgt scikit-learn einen flexiblen Ansatz. In scikit-learn kann man dies mit den Meta-Estimators oder Wrappern ermöglichen. Einige der Single-Output-Estimators kann man für Multi-Output-Szenarien anpassen.
Ein simple Alternative besteht darin, für jede Zielvariable ein eigenes, unabhängiges Modell zu trainieren und die Vorhersagen dann zu aggregieren. Darüber hinaus unterstützen einige Algorithmen in scikit-learn von Hause aus die Vorhersage mehrerer Ausgaben.
Die Fähigkeit, mehrere Ausgaben gemeinsam zu modellieren, ist besonders wertvoll, wenn zwischen den Zielvariablen Abhängigkeiten bestehen, da diese Korrelationen potenziell für genauere Vorhersagen genutzt werden können. Scikit-learn stellt hier ein praktisches Werkzeugset zur Verfügung, um komplexe Probleme mit mehreren Labeln anzugehen.
Meta-Estimators
Meta-Estimators sind im Grunde „Estimators“, die andere Estimators als Argumente verwenden. Sie erweitern oder modifizieren das Verhalten der zugrundeliegenden, sogenannten „Basis-Estimators“. Anstatt einen Algorithmus von Grund auf neu zu implementieren, um eine bestimmte Funktionalität zu erreichen ermöglicht ein Meta-Estimator die Wiederverwendung und Anpassung bestehender, oft einfacherer Estimators.
Ein gutes Beispiel hierfür ist MultiOutputClassifier. Dieser Meta-Estimator nimmt einen beliebigen Single-Output-Klassifikator (z.B. LogisticRegression oder SVC) und trainiert intern für jede einzelne Zielvariable ein separates Modell dieses Typs. Wenn dann eine Vorhersage für neue Daten erforderlich ist, werden die Eingabemerkmale an jedes der trainierten Modelle weitergeleitet, und die jeweiligen Vorhersagen werden in einem finalen Multi-Output-Vektor zusammengefasst.
Ein weiteres Beispiel für einen Meta-Estimator, der für Multi-Output-Probleme relevant ist, ist der ClassifierChain. Dieser geht über die einfache unabhängige Behandlung jeder Zielvariable hinaus. Er nimmt einen Basis-Klassifikator und trainiert eine Kette von Modellen. Das erste Modell in der Kette wird auf den ursprünglichen Merkmalen trainiert, um die erste Zielvariable vorherzusagen. Für das zweite Modell werden die ursprünglichen Merkmale zusammen mit der Vorhersage der ersten Zielvariable als Eingabe verwendet, um die zweite Zielvariable vorherzusagen. Dieser Prozess setzt sich fort, sodass die Vorhersage einer Zielvariable die Eingabe für die Vorhersage der nächsten Zielvariable in der Kette beeinflussen kann. Dies ermöglicht es, Abhängigkeiten zwischen den Zielvariablen zu modellieren.
Meta-Estimator Beispiel
Das folgende Beispiel zeigt eine Multi-Output Regression, bei der MultiOutputRegressor als Meta-Estimator verwendet wird, um einen GradientBoostingRegressor für jede Zielvariable einzusetzen.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.multioutput import MultiOutputRegressor
from sklearn.metrics import mean_squared_error, r2_score
# Erzeugung von synthetischen Multi-Output Regressionsdaten
# Datensatz mit 200 Samples, 5 Eingabemerkmalen und 3 Zielvariablen.
X, y = make_regression(n_samples=200, n_features=5, n_targets=3,
random_state=42, noise=10.0, effective_rank=None) # effective_rank=None für weniger korrelierte Targets
print(f"Form der Eingabemerkmale (X): {X.shape}")
print(f"Form der Zielvariablen (y): {y.shape}")
print(f"Beispiel Zielvariable y[0]: {y[0]}")
# Aufteilung der Daten in Trainings- und Testsets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# Definition des GradientBoostingRegressor als Basis-Estimator.
base_estimator = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
max_depth=3, random_state=0)
# Der MultiOutputRegressor wird als Meta-Estimator verwendet
# Er nimmt den base_estimator und wendet ihn auf jede Zielvariable an.
meta_estimator = MultiOutputRegressor(base_estimator)
# Der Meta-Estimator trainiert für jede der 3 Zielvariablen
# ein separates GradientBoostingRegressor-Modell
print("\nTraining des MultiOutputRegressor...")
meta_estimator.fit(X_train, y_train)
print("Training abgeschlossen.")
# Vorhersagen auf dem Testset
y_pred = meta_estimator.predict(X_test)
# Evaluierung
print("\nEvaluierung der Ergebnisse:")
for i in range(y_test.shape[1]): # Für jede Zielvariable
mse = mean_squared_error(y_test[:, i], y_pred[:, i])
r2 = r2_score(y_test[:, i], y_pred[:, i])
print(f" Zielvariable {i+1}:")
print(f" Mean Squared Error: {mse:.2f}")
print(f" R^2 Score: {r2:.2f}")
# Visualisierung der Ergebnisse mit Matplotlib
# Scatter-Plot für jede Zielvariable, der die wahren Werte gegen die vorhergesagten Werte zeigt.
n_targets = y_test.shape[1]
fig, axes = plt.subplots(1, n_targets, figsize=(5 * n_targets, 5), sharey=False) # sharey=False, da Skalen unterschiedlich sein können
if n_targets == 1: # Falls nur ein Target, axes ist kein Array
axes = [axes]
for i in range(n_targets):
ax = axes[i]
ax.scatter(y_test[:, i], y_pred[:, i], edgecolors=(0, 0, 0), alpha=0.7, label='Vorhersagen')
# Diagonale Linie für perfekte Vorhersage
min_val = min(np.min(y_test[:, i]), np.min(y_pred[:, i]))
max_val = max(np.max(y_test[:, i]), np.max(y_pred[:, i]))
ax.plot([min_val, max_val], [min_val, max_val], 'k--', lw=2, label='Perfekte Vorhersage')
ax.set_xlabel(f"Wahre Werte (Zielvariable {i+1})")
ax.set_ylabel(f"Vorhergesagte Werte (Zielvariable {i+1})")
ax.set_title(f"Vorhersage für Zielvariable {i+1}")
ax.legend()
ax.grid(True)
plt.suptitle("Multi-Output Regression mit MultiOutputRegressor und Gradient Boosting", fontsize=16, y=1.02)
plt.tight_layout(rect=[0, 0, 1, 0.98]) # rect um Platz für suptitle zu lassen
plt.show()Mit der Funktion make_regression wird zu Beginn des Skripts ein Datensatz mit 200 Datenpunkten (n_samples=200) erzeugt. Jeder Datenpunkt besitzt 5 Features (n_features=5) und 3 voneinander unabhängige Zielvariablen (n_targets=3). Im nächsten Schritt werden die generierten Daten mithilfe von train_test_split in einen Trainings- und einen Test-Datensatz aufgeteilt. Als Basis-Modell wird ein GradientBoostingRegressor mit 100 Bäumen (n_estimators=100), einer Lernrate von 0.1 und einer maximalen Tiefe von 3 für jeden Baum initialisiert. Darauf aufbauend wird ein MultiOutputRegressor erstellt der als Meta-Estimator fungiert. Er fungiert als eine Art Manager, der die Anwendung des Basis-Estimators auf die Multi-Output-Struktur koordiniert. Das Training des Modells erfolgt durch den Aufruf der fit-Methode mit X_train und y_train. Intern sorgt der MultiOutputRegressor dafür, dass drei unabhängige GradientBoostingRegressor-Modelle trainiert werden, eines für jede Spalte in y_train. Nachdem das Training abgeschlossen ist, wird die predict-Methode des trainierten meta_estimators verwendet, um Vorhersagen für die Eingabemerkmale des Testsets (X_test) zu generieren. Das Ergebnis y_pred ist eine Matrix, die für jeden Datenpunkt im Testset die vorhergesagten Werte für alle drei Zielvariablen enthält. Zur Beurteilung der Qualität der Vorhersagen, wird für jede Zielvariable der MSE und der R² Score berechnet und mit den Zielvariablen y_test verglichen.
Ergebnis:
Form der Eingabemerkmale (X): (200, 5)
Form der Zielvariablen (y): (200, 3)
Beispiel Zielvariable y[0]: [-49.00611675 -71.93412276 17.25030099]
Training des MultiOutputRegressor...
Training abgeschlossen.
Evaluierung der Ergebnisse:
Zielvariable 1:
Mean Squared Error: 763.56
R^2 Score: 0.94
Zielvariable 2:
Mean Squared Error: 1166.33
R^2 Score: 0.94
Zielvariable 3:
Mean Squared Error: 2222.77
R^2 Score: 0.92
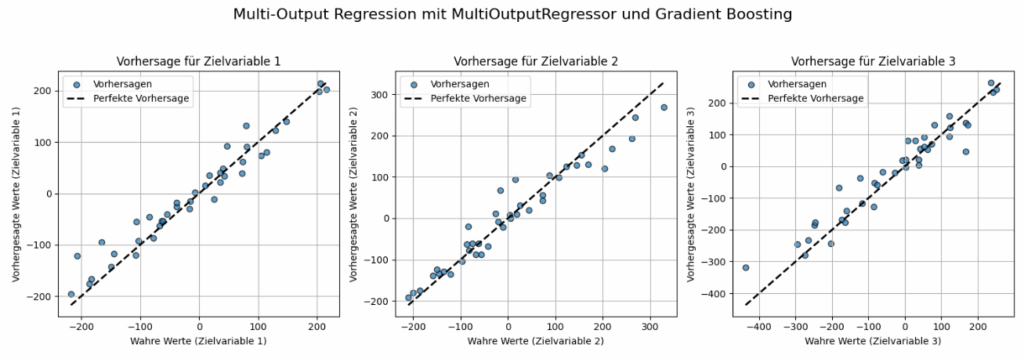
Das Bild zeigt die Ergebnisse der Multi-Output-Regressionsanalyse, die mit einem MultiOutputRegressor in Kombination mit Gradient Boosting durchgeführt wurde. Es besteht aus drei separaten Streudiagrammen, wobei jedes Diagramm die Vorhersagegüte für eine der drei Zielvariablen visualisiert. Die x-Achse stellt die „Wahren Werte“ der jeweiligen Zielvariable dar, also die tatsächlichen, korrekten Werte aus dem Testdatensatz. Die y-Achse zeigt die „Vorhergesagten Werte“ der jeweiligen Zielvariable, also die Werte, die das trainierte Modell für den Testdatensatz prognostiziert hat. Jeder blaue Punkt („Vorhersagen“) repräsentiert einen einzelnen Datenpunkt aus dem Testdatensatz, wobei seine Position durch den wahren Wert (x-Koordinate) und den vorhergesagten Wert (y-Koordinate) bestimmt wird. Die gestrichelte schwarze Diagonallinie („Perfekte Vorhersage“) stellt eine ideale Vorhersage dar. Wenn alle blauen Punkte genau auf dieser Linie lägen, hätte das Modell perfekt vorhergesagt.
Das Bild demonstriert, dass der gewählte Ansatz (MultiOutputRegressor mit Gradient Boosting) in der Lage ist, für alle drei Zielvariablen sinnvolle und relativ genaue Vorhersagen zu treffen.
ClassifierChain Beispiel
ClassifierChain ist ein weiterer Meta-Estimator in scikit-learn, der speziell für Multi-Output-Klassifikationsaufgaben entwickelt wurde, bei denen die Reihenfolge der Klassifikation eine Rolle spielen kann und die Vorhersage für eine Zielvariable als Merkmal für die nächste verwendet wird.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_multilabel_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.multioutput import ClassifierChain, MultiOutputClassifier
from sklearn.metrics import accuracy_score, hamming_loss, jaccard_score, confusion_matrix, ConfusionMatrixDisplay
# Erzeugung von synthetischen Multi-Label Klassifikationsdaten
X, y = make_multilabel_classification(n_samples=200, n_features=10,
n_classes=3, n_labels=2,
allow_unlabeled=False,
random_state=42)
print(f"Form der Eingabemerkmale (X): {X.shape}")
print(f"Form der Zielvariablen (y): {y.shape}")
print("Beispiel Zielvariablen (erste 5 Samples):")
print(y[:5])
# Aufteilung der Daten in Trainings- und Testsets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)
# Definition des Basis-Klassifikators
base_classifier = LogisticRegression(solver='liblinear', random_state=0)
# Definition der ClassifierChain
chain_order = [0, 1, 2]
classifier_chain = ClassifierChain(base_classifier, order=chain_order, random_state=42)
print("\nTraining der ClassifierChain...")
classifier_chain.fit(X_train, y_train)
print("Training abgeschlossen.")
y_pred_chain = classifier_chain.predict(X_test)
# Metriken für ClassifierChain
subset_accuracy_chain = classifier_chain.score(X_test, y_test)
hamming_chain = hamming_loss(y_test, y_pred_chain)
jaccard_chain = jaccard_score(y_test, y_pred_chain, average='samples')
accuracies_chain_per_label = [accuracy_score(y_test[:, i], y_pred_chain[:, i]) for i in range(y_test.shape[1])]
print("\n--- ClassifierChain Metriken ---")
print(f"Subset Accuracy: {subset_accuracy_chain:.2f}")
print(f"Hamming Loss: {hamming_chain:.2f}")
print(f"Jaccard Score (Samples Avg): {jaccard_chain:.2f}")
for i, acc in enumerate(accuracies_chain_per_label):
print(f" Genauigkeit für Zielvariable {i+1}: {acc:.2f}")
# MultiOutputClassifier (zum Vergleich)
multi_output_clf = MultiOutputClassifier(base_classifier)
print("\nTraining des MultiOutputClassifier...")
multi_output_clf.fit(X_train, y_train)
print("Training abgeschlossen.")
y_pred_multi = multi_output_clf.predict(X_test)
# Metriken für MultiOutputClassifier
subset_accuracy_multi = multi_output_clf.score(X_test, y_test)
hamming_multi = hamming_loss(y_test, y_pred_multi)
jaccard_multi = jaccard_score(y_test, y_pred_multi, average='samples')
accuracies_multi_per_label = [accuracy_score(y_test[:, i], y_pred_multi[:, i]) for i in range(y_test.shape[1])]
print("\n--- MultiOutputClassifier Metriken ---")
print(f"Subset Accuracy: {subset_accuracy_multi:.2f}")
print(f"Hamming Loss: {hamming_multi:.2f}")
print(f"Jaccard Score (Samples Avg): {jaccard_multi:.2f}")
for i, acc in enumerate(accuracies_multi_per_label):
print(f" Genauigkeit für Zielvariable {i+1}: {acc:.2f}")
# Visualisierung der Ergebnisse
n_labels = y_test.shape[1]
labels = [f"Label {i+1}" for i in range(n_labels)]
# Plot 1: Genauigkeit pro Label
plt.figure(figsize=(10, 6))
bar_width = 0.35
index = np.arange(n_labels)
rects1 = plt.bar(index - bar_width/2, accuracies_chain_per_label, bar_width,
label='ClassifierChain', color='skyblue')
rects2 = plt.bar(index + bar_width/2, accuracies_multi_per_label, bar_width,
label='MultiOutputClassifier (Unabhängig)', color='lightcoral')
plt.xlabel('Zielvariable (Label)')
plt.ylabel('Genauigkeit')
plt.title('Genauigkeit pro Label: ClassifierChain vs. Unabhängige Modelle')
plt.xticks(index, labels)
plt.ylim(0, 1.05)
plt.legend()
plt.grid(axis='y', linestyle='--')
plt.tight_layout()
plt.show()
# Plot 2: Vergleich der Gesamtmetriken (Hamming Loss und Jaccard Score)
metrics_names = ['Hamming Loss\n(niedriger ist besser)', 'Jaccard Score\n(höher ist besser)']
chain_scores = [hamming_chain, jaccard_chain]
multi_scores = [hamming_multi, jaccard_multi]
plt.figure(figsize=(10, 6))
index_metrics = np.arange(len(metrics_names))
rects_chain = plt.bar(index_metrics - bar_width/2, chain_scores, bar_width,
label='ClassifierChain', color='deepskyblue')
rects_multi = plt.bar(index_metrics + bar_width/2, multi_scores, bar_width,
label='MultiOutputClassifier', color='salmon')
plt.ylabel('Metrikwert')
plt.title('Vergleich der Gesamt-Klassifikationsmetriken')
plt.xticks(index_metrics, metrics_names)
plt.legend()
plt.grid(axis='y', linestyle='--')
# Textlabels auf den Balken hinzufügen
def autolabel(rects):
for rect in rects:
height = rect.get_height()
plt.annotate(f'{height:.2f}',
xy=(rect.get_x() + rect.get_width() / 2, height),
xytext=(0, 3), # 3 Punkte vertikaler Offset
textcoords="offset points",
ha='center', va='bottom')
autolabel(rects_chain)
autolabel(rects_multi)
plt.tight_layout()
plt.show()
# Plot 3: Konfusionsmatrizen pro Label für ClassifierChain
fig, axes = plt.subplots(1, n_labels, figsize=(5 * n_labels, 4.5))
if n_labels == 1: # Falls nur ein Label, ist axes kein Array
axes = [axes]
for i in range(n_labels):
cm = confusion_matrix(y_test[:, i], y_pred_chain[:, i])
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=[0, 1]) # Annahme: Klassen sind 0 und 1
disp.plot(ax=axes[i], cmap=plt.cm.Blues)
axes[i].set_title(f'Konfusionsmatrix\nLabel {i+1} (Chain)')
plt.suptitle("Konfusionsmatrizen für ClassifierChain pro Label", fontsize=16, y=1.03)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()Erläuterung:
Zunächst wird ein synthetischer Datensatz für die Multi-Label-Klassifikation generiert. Dieser Datensatz besteht aus 200 Datenpunkten, von denen jeder durch 10 Eingabemerkmale charakterisiert ist. Ziel ist es, für jeden Datenpunkt eine Zuweisung zu drei möglichen binären Labels (Klassen) vorherzusagen, wobei im Durchschnitt zwei Labels pro Datenpunkt aktiv sind. Anschließend werden die Daten in Trainings- und Testmengen aufgeteilt. Als Basis-Algorithmus für die Klassifikation dient in diesem Beispiel eine LogisticRegression.
Für den ClassifierChain-Ansatz wird zunächst eine spezifische Reihenfolge (chain_order = [0, 1, 2]) für die Klassifikatoren in der Kette festgelegt. Dies bedeutet, dass das Modell für das erste Label (Index 0) auf den ursprünglichen Merkmalen trainiert wird. Die Vorhersage dieses ersten Modells wird dann als zusätzliches Merkmal für das Training des Modells für das zweite Label (Index 1) verwendet. Dieser Prozess setzt sich fort, sodass die Vorhersage für das dritte Label (Index 2) sowohl die ursprünglichen Merkmale als auch die Vorhersagen der ersten beiden Labels berücksichtigt. Die ClassifierChain wird mit dem Basis-Klassifikator in der festgelegten Reihenfolge initialisiert. Mit der fit-Methode wird die Kette mit den Trainingsdaten trainiert und mit der predict-Methode eine Vorhersage für den Testdaten erstellt.
Zur Bewertung der Leistung des ClassifierChain werden mehrere Metriken berechnet. Die „Subset Accuracy“ gibt den Anteil der Testdaten an, bei denen alle Labels exakt korrekt vorhergesagt wurden. Der „Hamming Loss“ repräsentiert den durchschnittlichen Anteil der falsch klassifizierten Labels pro Datenpunkt. Der „Jaccard Score„, hier als Durchschnitt über die Samples berechnet, misst die Ähnlichkeit zwischen den tatsächlichen und vorhergesagten Label-Sets.
Parallel dazu wird der MultiOutputClassifier als Vergleichsmodell eingesetzt. Nach dem Training des MultiOutputClassifier auf denselben Trainingsdaten werden ebenfalls Vorhersagen für das Testset generiert. Für diesen Ansatz werden die gleichen Metriken – Subset Accuracy, Hamming Loss, Jaccard Score und die Genauigkeiten pro Label – berechnet und ausgegeben, um einen direkten Leistungsvergleich mit dem ClassifierChain zu ermöglichen. Dieser Vergleich hilft zu beurteilen, ob die explizite Modellierung von Abhängigkeiten zwischen den Labels durch die ClassifierChain zu einer Verbesserung der Vorhersagequalität führt.
Ausgabe:
Form der Eingabemerkmale (X): (200, 10) Form der Zielvariablen (y): (200, 3) Beispiel Zielvariablen (erste 5 Samples): [[1 1 0] [1 1 0] [0 0 1] [1 1 1] [0 1 0]] Training der ClassifierChain... Training abgeschlossen. --- ClassifierChain Metriken --- Subset Accuracy: 0.76 Hamming Loss: 0.08 Jaccard Score (Samples Avg): 0.90 Genauigkeit für Zielvariable 1: 0.88 Genauigkeit für Zielvariable 2: 0.94 Genauigkeit für Zielvariable 3: 0.94 Training des MultiOutputClassifier... Training abgeschlossen. --- MultiOutputClassifier Metriken --- Subset Accuracy: 0.78 Hamming Loss: 0.07 Jaccard Score (Samples Avg): 0.91 Genauigkeit für Zielvariable 1: 0.88 Genauigkeit für Zielvariable 2: 0.94 Genauigkeit für Zielvariable 3: 0.96
Das Beispiel liefert einen Vergleich der Leistung zwischen dem ClassifierChain und dem MultiOutputClassifier auf demselben Testdatensatz.
- Subset Accuracy
ClassifierChain: 0.76
MultiOutputClassifier: 0.78
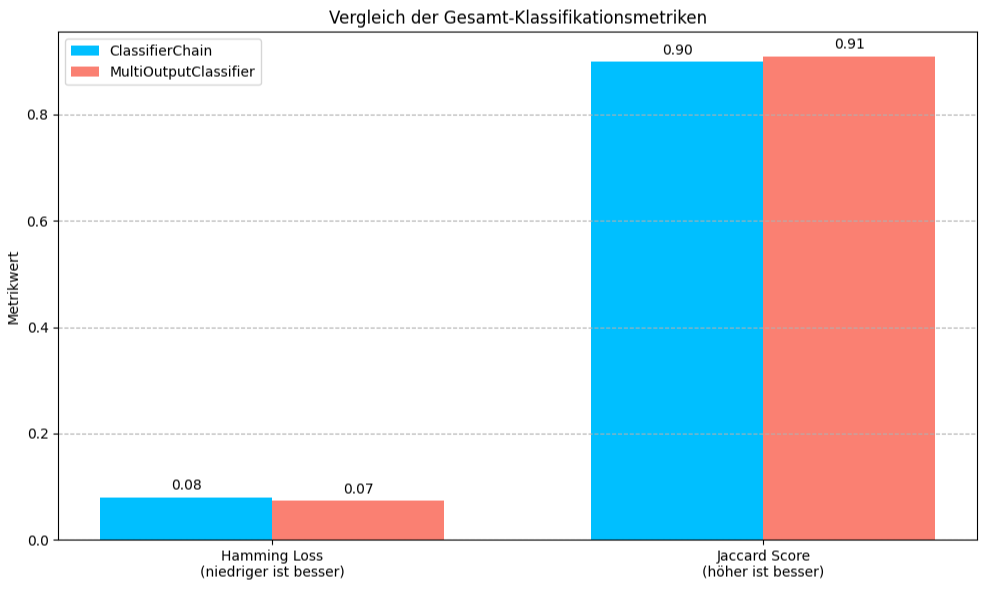
Der MultiOutputClassifier erreicht eine leicht höhere Subset Accuracy. Das bedeutet, er hat bei einem etwas größeren Anteil der Test-Samples alle Labels exakt korrekt vorhergesagt. - Hamming Loss
ClassifierChain: 0.08
MultiOutputClassifier: 0.07
Der MultiOutputClassifier hat einen niedrigeren Hamming Loss. Dies bedeutet, dass er im Durchschnitt einen geringeren Anteil an falsch klassifizierten einzelnen Labels aufweist. - Jaccard Score (Samples Avg)
ClassifierChain: 0.90
MultiOutputClassifier: 0.91
Auch hier erzielt der MultiOutputClassifier einen leicht höheren Jaccard Score. Dies deutet auf eine etwas bessere Übereinstimmung zwischen den vorhergesagten und den tatsächlichen Label-Sets pro Sample hin. - Genauigkeit pro Zielvariable
- Zielvariable 1: Beide Methoden erreichen 0.88.
- Zielvariable 2: Beide Methoden erreichen 0.94.
- Zielvariable 3: ClassifierChain erreicht 0.94, während MultiOutputClassifier 0.96 erreicht. Hier ist der MultiOutputClassifier leicht besser.
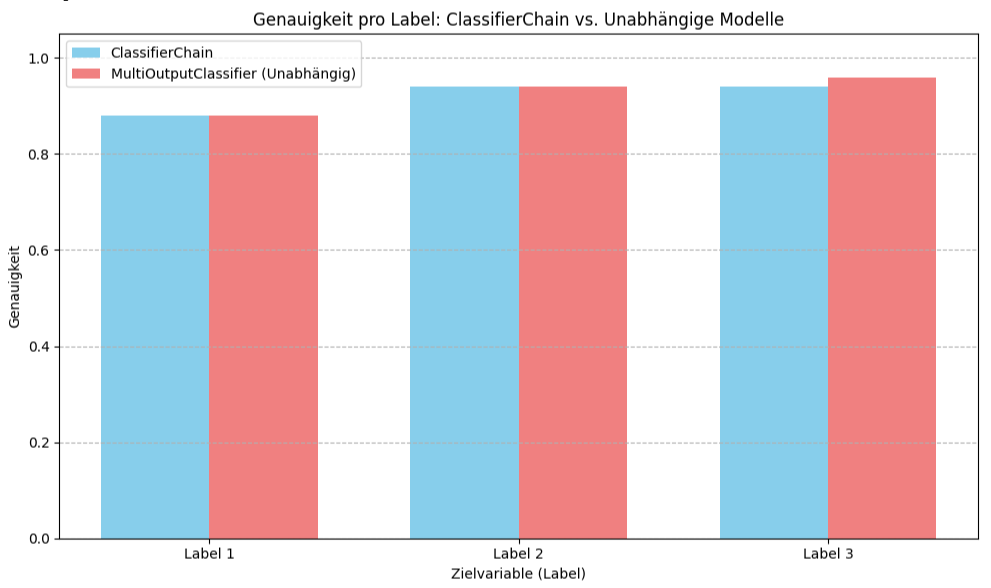
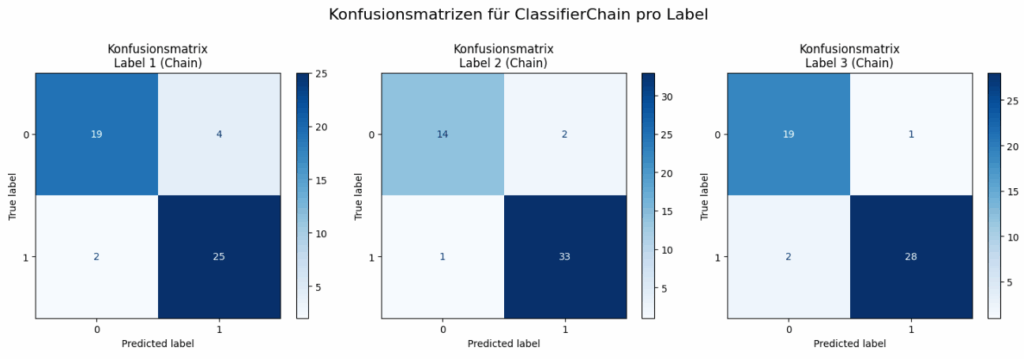
Der MultiOutputClassifier, der für jedes Label ein unabhängiges Modell trainiert, erzielt bessere Gesamtmetriken (Subset Accuracy, Hamming Loss, Jaccard Score) und ist bei der Genauigkeit für das dritte Label leicht überlegen, während er bei den anderen beiden Labels gleichauf liegt. Dies deutet darauf hin, dass für diesen Datensatz (und die gewählte Reihenfolge für die ClassifierChain) die Modellierung von Abhängigkeiten zwischen den Labels keinen Vorteil gegenüber dem einfacheren Ansatz der unabhängigen Behandlung der Labels gebracht hat.
