TODO für Tag 9
- RandomForestClassifier anwenden
- Vorteile gegenüber einzelnen Entscheidungsbäumen
- RandomizedSearchCV für RandomForest
RandomForestClassifier anwenden
Der RandomForestClassifier ist ein leistungsfähiger und vielseitiger Classifier.
Statt nur einen einzigen Entscheidungsbaum zu trainieren, baut der Random Forest viele Bäume auf zufälligen Daten-Subsets und Merkmals-Subsets auf. Das Ergebnis jedes Baums wird als Voting betrachtet, und die Klasse mit den meisten Votes wird als Gesamtergebnis ausgegeben.
Beispielcode
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# Daten laden
iris = load_iris()
X = iris.data
y = iris.target
# Trainings- und Testdaten aufteilen
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Random Forest-Modell erstellen
rf = RandomForestClassifier(n_estimators=100, random_state=42)
# Modell trainieren
rf.fit(X_train, y_train)
# Vorhersage treffen
y_pred = rf.predict(X_test)
# Genauigkeit berechnen
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")Der Python-Code lädt einmal mehr den Iris-Datensatz :-), teilt ihn in Trainings- und Testdaten auf und trainiert damit ein Random Forest Klassifizierungsmodell auf den Trainingsdaten.
Mit der predict Funktion macht er eine Vorhersage auf den Testdaten und bewertet schließlich die Leistung des Modells, indem die Genauigkeit der Vorhersagen im Vergleich zu den tatsächlichen Labels berechnet und ausgegeben wird.
Accuracy: 1.00
Um die Feature Importance eines Random Forest Modells in einem Plot darzustellen, kann mandie feature_importances_-Eigenschaft des trainierten Modells verwenden. Diese Eigenschaft gibt die Wichtigkeit jedes Merkmals im Modell an. Man kann diese Werte visualisieren, um zu sehen, welche Merkmale den größten Einfluss auf die Vorhersagen haben.
Hier ein Beispiel, das auch die Feature Importance in einem Balkendiagramm darstellt:
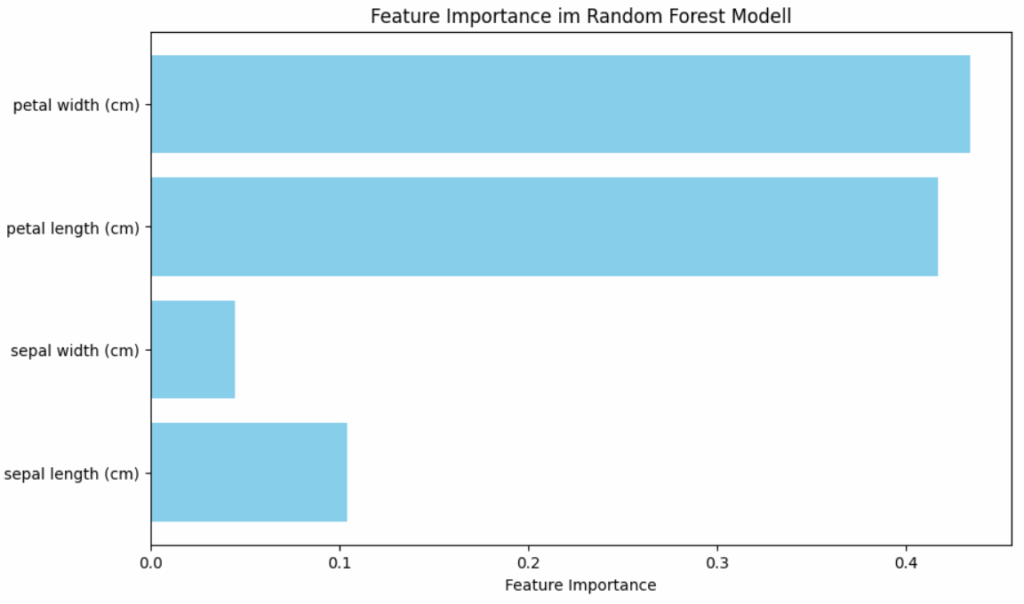
Das Diagramm zeigt die Wichtigkeit jedes Merkmals im Iris-Datensatz. Merkmale mit höheren Balken tragen stärker zur Vorhersage des Modells bei. Hier ist, was die Darstellung aussagt:
- Wichtigkeitsskala
Die horizontale Achse („Feature Importance“) zeigt einen Wert zwischen 0.0 und ca. 0.45. Ein höherer Wert auf dieser Skala bedeutet, dass das entsprechende Merkmal als wichtiger für die korrekte Klassifizierung der Iris-Arten angesehen wurde. - Ranking der Merkmale
Die Darstellung sortiert die Merkmale (oft absteigend, hier durch die Balkenlänge visuell offensichtlich) nach ihrer Wichtigkeit
- petal width (cm)
Dieses Merkmal hat den höchsten Wichtigkeitswert (ca. 0.43). Es ist das wichtigste Merkmal für dieses Modell, um die Iris-Arten zu unterscheiden. - petal length (cm)
Dieses Merkmal ist das zweitwichtigste (ca. 0.41), sehr nah an der „petal width“. - sepal length (cm)
Dieses Merkmal ist deutlich weniger wichtig (ca. 0.1). - sepal width (cm)
Dies ist das am wenigsten wichtige Merkmal (ca. 0.02-0.03) im Vergleich zu den anderen dreien.
- petal width (cm)
- Aussagekraft der Merkmale
Die Darstellung macht deutlich, dass petal (Länge und Breite) weitaus aussagekräftiger für die Unterscheidung der Iris-Arten sind als die sepal (Länge und Breite). Insbesondere die „sepal width“ scheint für dieses Modell von sehr geringer Bedeutung zu sein.
Für das trainierte Random Forest Modell sind die Breite und Länge der Blütenblätter die entscheidenden Faktoren, um die jeweilige Iris-Art korrekt zu identifizieren. Die Maße der Kelchblätter sind weniger relevant für diese Klassifizierungsaufgabe.
Vorteile gegenüber einzelnen Entscheidungsbäumen
Der RandomForestClassifier ist eine Methode, die auf einer Sammlung von vielen einzelnen Entscheidungsbäumen basiert. Seine Vorteile gegenüber einem einzelnen Entscheidungsbaum ergeben sich hauptsächlich aus dieser Kombination und der Art und Weise, wie die Bäume im Wald erstellt werden.
Reduzierung von Overfitting
Dies ist der wichtigste Vorteil. Ein einzelner, tiefer Entscheidungsbaum kann das Trainingsrauschen lernen und sich stark an die Trainingsdaten anpassen, was zu schlechter Leistung auf unbekannten Daten führt. Ein Random Forest trainiert viele Bäume auf leicht unterschiedlichen Datensätzen und verwendet bei jeder Aufteilung im Baum nur eine zufällige Teilmenge der Features. So werden die Vorhersagen vieler solcher weniger überangepasster Bäume gemittelt oder per Mehrheitsentscheid kombiniert. So wird die Gesamtvarianz des Modells stark reduziert, was zu einer besseren Generalisierung auf neue Daten führt.
Verbesserte Genauigkeit
Aufgrund der reduzierten Varianz und der Kombination der Stärken vieler Bäume erzielt ein Random Forest oft eine deutlich höhere Vorhersagegenauigkeit als ein einzelner Entscheidungsbaum, insbesondere bei komplexen Datensätzen.
Erhöhte Robustheit und Stabilität
Ein einzelner Entscheidungsbaum kann sehr empfindlich auf kleine Änderungen in den Trainingsdaten reagieren. Wenn sich die Trainingsdaten leicht ändern, kann die Struktur des Baumes komplett anders aussehen. Da ein Random Forest die Vorhersagen vieler Bäume kombiniert, wird die Auswirkung von Änderungen auf einzelne Bäume geglättet. Das Gesamtmodell ist dadurch stabiler und weniger anfällig für Schwankungen in den Trainingsdaten.
Umgang mit hochdimensionalen Daten
Random Forests können auch mit Datensätzen arbeiten, die sehr viele Merkmale (Features) haben. Die zufällige Auswahl von Features bei jeder Aufteilung macht sie relativ effizient.
Automatische Feature Importance
Wie im gezeigten Plot zu sehen ist, liefert der Random Forest von Haus aus einen Wert für die Wichtigkeit der einzelnen Features, der Aufschluss darüber gibt, welche Merkmale am meisten zur Vorhersage beitragen. Ein einzelner Baum liefert diese Information zwar auch, aber der Wert aus einem Ensemble ist oft robuster.
Nachteile gegenüber einzelnen Entscheidungsbäumen
Geringere Interpretierbarkeit
Ein einzelner Entscheidungsbaum lässt sich leicht visualisieren und nachvollziehen („Wenn Merkmal A > X und Merkmal B < Y, dann Klasse Z“). Ein Random Forest mit 100 Bäumen ist viel schwieriger zu interpretieren; man weiß, dass er eine gute Vorhersage macht, aber nicht so einfach warum.
Höherer Rechenaufwand
Das Trainieren von 100 oder mehr Bäumen dauert länger und benötigt mehr Speicher als das Trainieren eines einzelnen Baumes.
Hyperparameter-Optimierung mit RandomizedSearchCV
RandomizedSearchCV ist eine Technik zur Hyperparameter-Optimierung in scikit-learn, die anstatt alle möglichen Kombinationen wie bei GridSearchCV auszuprobieren, nur eine feste Anzahl zufällig ausgewählter Kombinationen testet. So lässt sich die Suche nach guten Parametern beschleunigen. Besonders Modelle mit vielen einstellbaren Parametern wie Random Forests können davon profitieren, da eine vollständige Suche schnell sehr aufwändig wird. RandomizedSearchCV ist also besonders nützlich, wenn Rechenzeit begrenzt ist.
Beispiel: RandomizedSearchCV für RandomForest
import matplotlib.pyplot as plt
import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import RandomizedSearchCV
from sklearn.datasets import load_iris
from scipy.stats import randint
# Datensatz laden
X, y = load_iris(return_X_y=True)
# Modell
rf = RandomForestClassifier(random_state=42)
# Hyperparameter-Suchraum
param_dist = {
'n_estimators': randint(100, 300),
'max_depth': randint(10, 30),
'min_samples_split': randint(2, 20),
'min_samples_leaf': randint(1, 20),
'max_features': ['auto', 'sqrt', 'log2']
}
# RandomizedSearchCV Setup
rscv = RandomizedSearchCV(
rf,
param_distributions=param_dist,
n_iter=50, # 50 Kombinationen ausprobieren
cv=5, # 5-fache Kreuzvalidierung
verbose=0, # leiser
random_state=42,
n_jobs=-1
)
# Modell trainieren
rscv.fit(X, y)
# Ergebnisse extrahieren
results = rscv.cv_results_
mean_test_scores = results['mean_test_score']
param_n_estimators = [d['n_estimators'] for d in results['params']]
param_max_depth = [d['max_depth'] for d in results['params']]
# Scatter Plot: n_estimators vs. Score (farbig nach max_depth)
plt.figure(figsize=(10, 6))
scatter = plt.scatter(param_n_estimators, mean_test_scores, c=param_max_depth, cmap='viridis', edgecolor='k')
plt.colorbar(scatter, label='max_depth')
plt.xlabel('n_estimators')
plt.ylabel('Mean Test Score (CV)')
plt.title('RandomizedSearchCV Ergebnisse für RandomForestClassifier')
plt.grid(True)
plt.show()
# Beste Parameter ausgeben
print(f"Bester Score: {rscv.best_score_:.2f}")
print(f"Beste Parameter: {rscv.best_params_}")Ausgabe:
Bester Score: 0.97
Beste Parameter: {'max_depth': 15, 'max_features': 'sqrt', 'min_samples_leaf': 1, 'min_samples_split': 13, 'n_estimators': 157}
Das beste gefundene Random Forest Modell, das während der RandomizedSearchCV getestet wurde, erreicht eine mittlere Kreuzvalidierungsgenauigkeit von 97 %. Das bedeutet, dass dieses Modell auf den Trainings-/Validierungsdaten im Durchschnitt 97 % der Fälle korrekt klassifiziert hat.
Folgende Hyperparameter wurden als optimal ermittelt:
max_depth: 15bedeutet, dass die Entscheidungsbäume maximal 15 Ebenen tief wachsen dürfen.max_features: 'sqrt'heißt, dass bei jedem Split nur die Quadratwurzel der Gesamtzahl der Features betrachtet wird.min_samples_leaf: 1bedeutet, dass Blätter mindestens ein Sample enthalten dürfen.min_samples_split: 13besagt, dass ein Knoten mindestens 13 Samples haben muss, bevor er gesplittet werden darf.n_estimators: 157legt fest, dass der Random Forest aus 157 Bäumen besteht.
Neben der Ausgabe erhält man auch die folgende Warnung
FitFailedWarning:
80 fits failed out of a total of 250.
The score on these train-test partitions for these parameters will be set to nan.
If these failures are not expected, you can try to debug them by setting error_score='raise'.
Die FitFailedWarning bedeutet, dass 80 von insgesamt 250 Modellanpassungen fehlgeschlagen sind. Das passiert, wenn bestimmte zufällig gewählte Hyperparameterkombinationen dazu führen, dass das Modell nicht korrekt trainiert oder validiert werden kann, etwa weil die Konfiguration mathematisch unsinnig oder technisch inkompatibel ist. In solchen Fällen setzt scikit-learn die Bewertungsergebnisse dieser fehlgeschlagenen Fits einfach auf NaN, um den Suchvorgang nicht abzubrechen und dennoch möglichst viele brauchbare Modelle zu testen.
Man kann das Verhalten des RandomizedSearchCV ändern, indem man error_score='raise' setzt, wodurch beim ersten auftretenden Fehler eine Exception ausgelöst wird und man so direkt die Ursache analysieren kann.
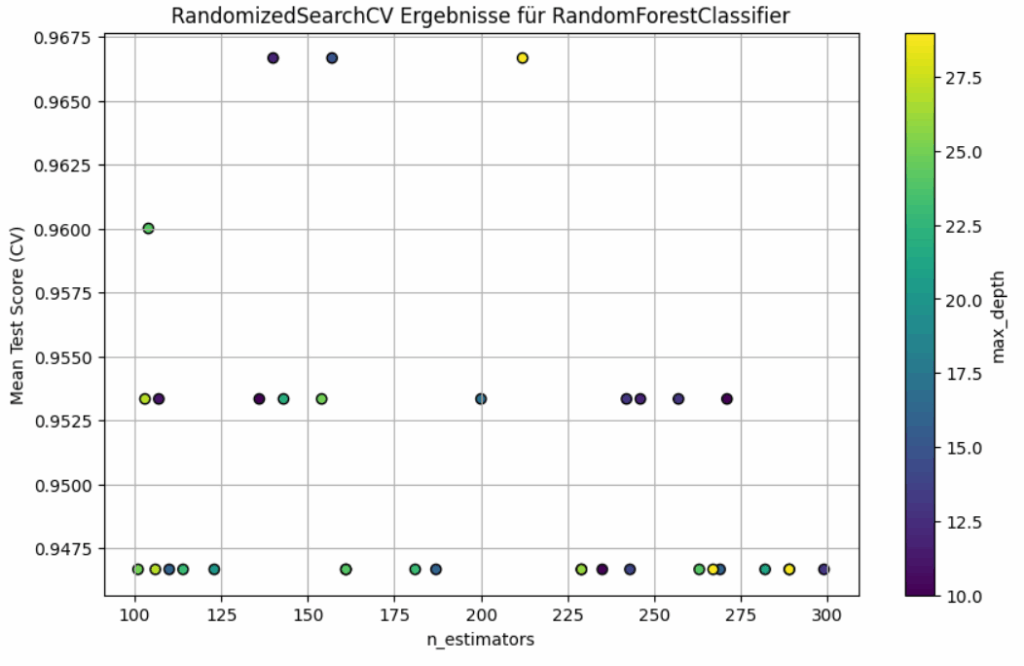
In dem Plot siehst sieht man der X-Achse die Anzahl der Bäume (n_estimators) und auf der Y-Achse den mittleren Cross-Validation-Score (Mean Test Score (CV)) für jede getestete Hyperparameterkombination. Jeder Punkt stellt ein Ergebnis eines RandomizedSearchCV-Durchlaufs dar, wobei die Farbe des Punktes die maximale Tiefe der Bäume (max_depth) codiert, wie in der Farbleiste rechts dargestellt. Auffällig ist, dass die meisten Modelle relativ nahe beieinanderliegende Scores erreichen, meist im Bereich zwischen 0,947 und 0,968, unabhängig von der Anzahl der Bäume. Einzelne Konfigurationen mit höheren max_depth-Werten (hellere Farben) tendieren leicht zu besseren Scores, aber insgesamt zeigt der Plot, dass die Optimierung durch mehr Bäume allein nur begrenzt zusätzlichen Nutzen bringt. Eine echte Verbesserung scheint eher von einer passenden Kombination aus Baumanzahl und Tiefe abzuhängen, wobei extrem viele Bäume nicht automatisch bessere Ergebnisse liefern. Der Plot macht klar: Es gibt einen Punkt, an dem mehr Bäume oder größere Tiefe keinen spürbaren Gewinn mehr bringen.
