TODO Für Tag 12
- SVC verwenden
- Kernel verstehen
SVC (Support Vector Classification)
SVC ist eine Implementierung von Support Vector Machines (SVM) für Klassifikationsaufgaben. Die zugrunde liegenden Konzepte basieren auf der Idee, eine optimale Trennlinie zwischen Klassen zu finden. Dabei maximiert die SVM den Abstand zwischen dieser Trennlinie und den nächstgelegenen Punkten beider Klassen (Support Vektors).
Kernel verstehen
Ein Kernel ist eine Funktion die das Skalarprodukt zweier Punkte in einem höherdimensionalen Raum darstellt, ohne die Punkte explizit zu transformieren. In scikit-learn sind folgende Kernel vorhanden.
Linear Kernel
Der Linear-Kernel trennt die Daten mit einer einfachen geraden Linie (oder einer Ebene im mehrdimensionalen Raum). Er sagt im Grunde: „Ich suche nach einer Linie/Ebene, die die zwei Gruppen möglichst klar voneinander trennt.“ Der Linear Kernel kann verwendet werden, wenn die Daten relativ sauber ohne große Kurven oder Muster trennbar sind.
Polynomial Kernel
Statt einer geraden Linie erlaubt dieser Kernel gekrümmte Trennlinien, je nachdem, wie hoch der Polynomgrad ist. Ein Grad-2-Polynom ergibt z. B. eine U- oder S-förmige Grenze. Der Polynomial Kernel kann verwendet werden, wenn die Daten ein gewisses Muster haben, das nicht linear ist – z. B. wenn die Gruppen voneinander geschwungen getrennt sind oder sich umschlingen.
RBF (Radial Basis Function) Kernel
Der RBF-Kernel arbeitet mit dem Konzept von Einflusssphären um jeden Trainingspunkt. Er schaut sich an, wie nah ein neuer Punkt an den bekannten Punkten ist, und trifft auf dieser Basis Entscheidungen. Dadurch können auch sehr komplexe, verschlungene Trennungen entstehen. Wenn man keine Ahnung hat, wie die Trennung aussieht, oder wenn die Daten wirklich wild verteilt oder verworren sind kann der RBF Kernel verwendet werden.
Sigmoid Kernel
Der Sigmoid-Kernel misst die Beziehung zwischen zwei Punkten und entscheidet anhand eines „S-Kurven“-Verhaltens, ob sie zusammengehören oder nicht. Seine Trennlinien sind nicht so flexibel wie beim RBF, aber auch nicht starr gerade. Er ist manchmal gut, wenn man einen SVM wie ein kleines neuronales Netz nutzen will.
Beispiel:
from sklearn.svm import SVC
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.datasets import make_moons
# Beispiel-Daten (nicht linear trennbar)
X, y = make_moons(n_samples=1000, noise=0.2, random_state=42)
# Aufteilen in Trainings- und Testdaten
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Verschiedene Kernels testen
kernels = ['linear', 'poly', 'rbf', 'sigmoid']
for kernel in kernels:
print(f"\n--- Kernel: {kernel} ---")
model = SVC(kernel=kernel, degree=3, gamma='auto', C=1.0)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(classification_report(y_test, y_pred))
# Visualisierung der Entscheidungsgrenze
plt.figure(figsize=(6, 5))
h = .02
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=y, palette='coolwarm', edgecolor='k')
plt.title(f'SVC Decision Boundary with {kernel} kernel')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.tight_layout()
plt.show()Das demonstriert, wie sich unterschiedliche Kernel-Funktionen bei einem Support-Vector-Classifier (SVC) auswirken, indem ein nichtlinear trennbarer Datensatz verwendet wird und für jede Kernel-Art sowohl die Klassifikation als auch die Entscheidungsgrenze visualisiert wird.
Zunächst wird ein künstlicher Datensatz mit der Funktion make_moons generiert. Diese Daten enthalten zwei halbmondförmige Klassen, die sich nicht durch eine einfache Gerade trennen lassen. Danach werden die Daten in Trainings- und Testmenge aufgeteilt. Für jeden der vier Kernels – linear, polynomial, radial basis function und sigmoid wird ein eigenes SVC-Modell erstellt, trainiert und anschließend verwendet, um Vorhersagen für die Testdaten zu treffen. Die Klassifikationsergebnisse werden mithilfe von matplotlib ausgegeben. Für jeden der vier Kernels (linear, poly, rbf, sigmoid) werden zwei Dinge ausgegeben:
- Classification Report
Eine Tabelle mit Leistungskennzahlen für die Klassifizierung auf dem Testdatensatz - Plot der Entscheidungsgrenze
Eine Visualisierung, wie der trainierte SVC den Feature-Raum in Regionen einteilt, die den beiden Klassen zugeordnet sind. Die Punkte im Plot sind die Testdatenpunkte, eingefärbt nach ihrer tatsächlichen Klasse
Interpretation der Kennzahlen im Classification Report:
- precision
Wie viele der als Klasse X vorhergesagten Punkte waren tatsächlich Klasse X? (Präzision für Klasse 0 und Klasse 1). - recall
Wie viele der tatsächlichen Punkte der Klasse X wurden korrekt als Klasse X vorhergesagt? (Recall für Klasse 0 und Klasse 1). - f1-score
Der harmonische Mittelwert aus Präzision und Recall. Eine gute Metrik, wenn Präzision und Recall wichtig sind und die Klassen möglicherweise unausgeglichen sind. - support
Die Anzahl der tatsächlichen Punkte der Klasse X im Testdatensatz (hier 156 für Klasse 0 und 144 für Klasse 1, insgesamt 300 Testpunkte). - accuracy
Der Gesamtprozentsatz der korrekt klassifizierten Punkte im Testdatensatz.
Der Plot ist in zwei Farben unterteilt. Diese Farben repräsentieren die Regionen im Feature-Raum, die der SVC der Klasse 0 (Blau) bzw. der Klasse 1 (Orange) zuordnet sind. Die Linie (oder Kurve), die die blauen und roten Regionen trennt, ist die Entscheidungsgrenze. Die Punkte im Plot sind die tatsächlichen Datenpunkte aus den Testdaten. Blaue Punkte gehören tatsächlich zur Klasse 0, orangefarbene Punkte zur Klasse 1.
Ein guter Classifier hat eine Entscheidungsgrenze, die die blauen Punkte von den orangefarbenen Punkten trennt. Idealerweise liegen alle blauen Punkte in der blauen Region und alle orangefarbenen Punkte in der roten Region. Punkte, die auf der „falschen“ Seite der Grenze liegen, sind Fehlklassifikationen.
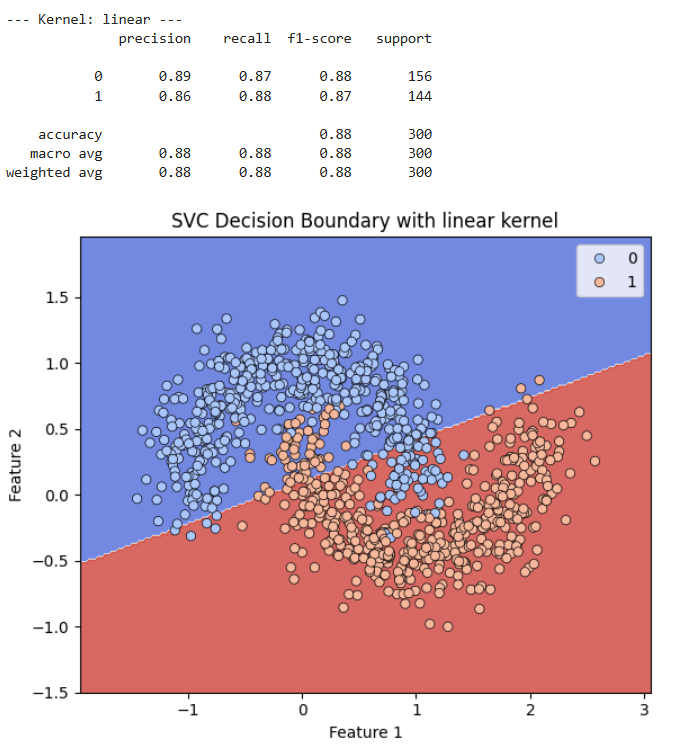
Linear Kernel
Die Entscheidungsgrenze ist eine gerade Linie. Da der Datensatz nicht linear trennbar ist, kann eine gerade Linie die beiden Klassen nicht gut trennen. Viele blaue Punkte liegen in der roten Region und viele rote Punkte in der blauen Region. Dies bestätigt die schlechtere Leistung des linearen Kernels für diesen Datensatz.
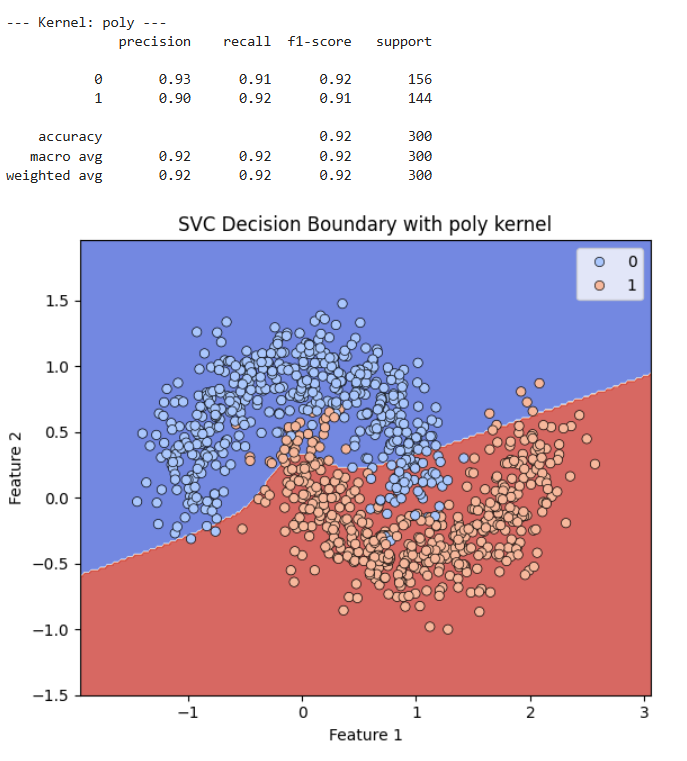
Poly Kernel
Die Entscheidungsgrenze ist eine leicht geschwungene Kurve. Sie versucht, die Form der „Halbmonde“ zu approximieren. Sie trennt die meisten Punkte korrekt, aber es gibt einige Fehlklassifikationen entlang der Grenze.
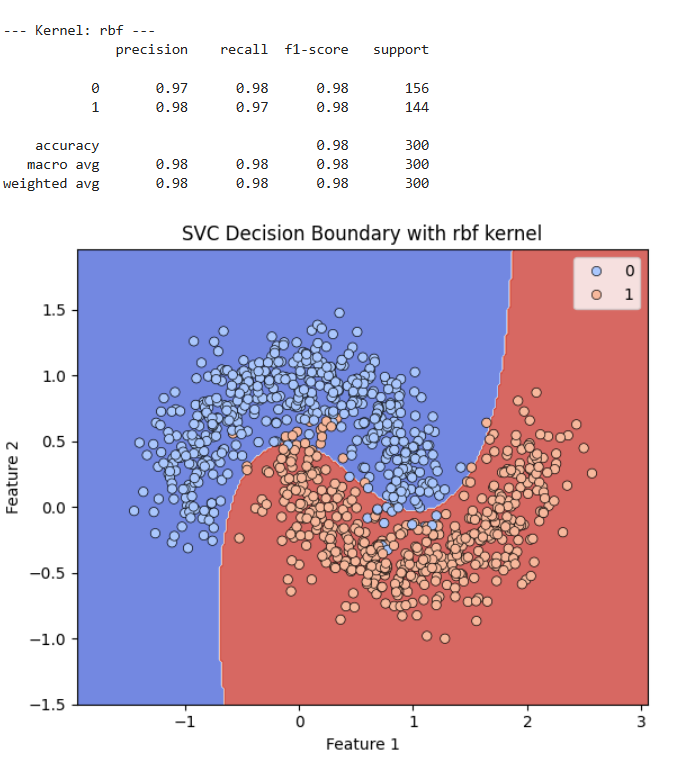
Rbf Kernel (Radial Basis Function)
Die Entscheidungsgrenze ist eine komplexe, sehr gut an die Form der „Halbmonde“ angepasste Kurve. Sie trennt die beiden Klassen fast perfekt. Kaum ein blauer Punkt liegt in der roten Region oder umgekehrt. Dies visuell untermauert die ausgezeichnete Leistung dieses Kernels auf diesem nicht-linearen Datensatz.
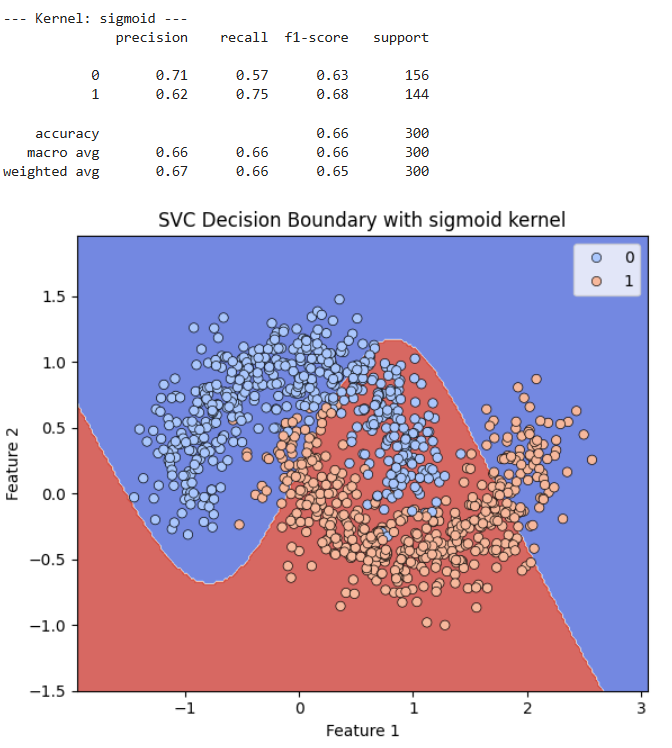
Sigmoid Kernel Die Entscheidungsgrenze ist eine gewellte Kurve, die jedoch die Struktur des Datensatzes nicht gut erfasst. Sie schneidet durch Bereiche beider Klassen was zu vielen Fehlklassifikationen führt. Dies erklärt die sehr schlechten Leistungskennzahlen.
Die Bilder zeigen, dass die Wahl des Kernel eine entscheidende Rolle für die Leistung eines SVCs spielt, insbesondere bei Datensätzen, die nicht linear trennbar sind. Der lineare Kernel ist am wenigsten geeignet, da er nur eine gerade Linie als Entscheidungsgrenze erzeugen kann. Der polynomielle Kernel kann gekrümmte Grenzen erzeugen und ist besser als der lineare Kernel. Der RBF Kernel ist hier am leistungsfähigsten, da er in der Lage ist, sehr komplexe und an die Daten angepasste nicht-lineare Entscheidungsgrenzen zu finden, die die Struktur des „Halbmond“-Datensatzes exzellent abbilden. Der sigmoid Kernel war für diesen spezifischen Datensatz auch nicht gut geeignet und führte zu einer schlechten Klassifizierung.
Wenn man die erzeugten Support-Vektoren anzeigen lassen möchte, kann man das mit model.support_vectors_ tun. In dem Array sind alle erstellten Support-Vektoren enthalten, die das Modell beim Training erstellt hat.
Neben den vordefinierten Kerneln kann man auch eigene Kernel definieren und die in dem SVC verwenden.
Das folgende Beispiel The following code defines a linear kernel and creates a classifier instance that will use that kernel: TODO
import numpy as np
from sklearn import svm
def my_kernel(X, Y):
return np.dot(X, Y.T)
clf = svm.SVC(kernel=my_kernel)