TODO Für Tag 13
- Erklärung und Vorteile von Pipeline
- Beispiel Pipeline mit Skalierung und Modell (StandardScaler und RandomForestClassifier)
- Auswertung der Ergebnisse
Erklärung und Vorteile von Pipeline
In scikit-learn sind Pipelines ein Konzept zur strukturierten und reproduzierbaren Modellierung von ML-Workflows. Sie dienen dazu, eine Abfolge von Verarbeitungsschritten (Vorverarbeitung, Feature-Transformation, Modelltraining, etc.) logisch miteinander zu verknüpfen. Eine Pipeline kapselt alle Schritte eines Prozesses, die typischerweise in einer festen Reihenfolge auf Trainings- und Testdaten angewendet werden, und stellt sicher, dass diese konsistent und korrekt ausgeführt werden. Dabei übernimmt sie nicht nur das Verketten der Verarbeitungsschritte, sondern sorgt auch dafür, dass die Parameter jedes Schrittes im Rahmen von Modelloptimierung oder Cross-Validation kontrolliert und verändert werden können.
Die Vorteile von Pipelines liegen unter anderem in der Vermeidung häufiger Fehlerquellen, z.B. dass Testdaten unbeabsichtigt in die Trainingsphase einfließen. Da eine Pipeline immer den gleichen Transformationsprozess auf Trainings- und Testdaten anwendet, stellt sie sicher, dass keine inkonsistente Verarbeitung stattfindet.
In der Praxis wird eine Pipeline in scikit-learn mit dem Pipeline-Objekt erstellt, das eine Folge von Verarbeitungsschritten enthält, wobei jeder Schritt aus einem Namen und einem Transformer oder Estimator besteht. Während Transformer für Aufgaben wie Standardisierung, One-Hot-Encoding oder Imputation zuständig sind, bildet der finale Schritt ein trainierbares Modell ab, beispielsweise ein Klassifikator oder Regressor. Beim Aufruf der Methode fit() wird die gesamte Pipeline durchlaufen. Erst werden alle Transformer auf die Trainingsdaten angewendet, anschließend wird das Modell auf den transformierten Daten trainiert. Für Vorhersagen wird dann die Methode predict() aufgerufen, wobei wiederum alle Schritte der Pipeline sequenziell auf die Daten angewendet werden.
Ein weiterer Vorteil ergibt sich bei der automatisierten Hyperparameteroptimierung, etwa mittels GridSearchCV oder RandomizedSearchCV. Durch die Einbettung der gesamten Pipeline in das Optimierungsverfahren können die Parameter des Modells und der Vorverarbeitung einbezogen werden. Dies ist ein wesentlicher Schritt in Richtung AutoML und robuster Modellierungsprozesse, bei denen nicht nur das Modell, sondern der gesamte Workflow systematisch verbessert wird.
Beispiel Pipeline mit Skalierung und Modell
Das folgende Beispiel lädt den schon bekannten Iris-Datensatz und teilt ihn in separate Trainings- und Testdatensätze. Als nächstes wird der StandardScaler und RandomForestClassifier in einer Pipeline zusammengefasst. Um die bestmögliche Leistung des RandomForestClassifier zu erzielen, werden dessen Hyperparameter mit dem RandomizedSearchCV optimiert. Die Suche probiert dabei verschiedene Parameterkombinationen (n_iter=100) aus und bewertet jede Kombination durch eine mehrfache Kreuzvalidierung (cv=10) auf dem Trainingsdatensatz, wobei die Genauigkeit als Bewertungsmetrik dient. Nachdem die Optimierung abgeschlossen ist, gibt das Skript die beste gefundene Parameterkombination aus und bewertet anschließend die Leistung des Modells, das mit diesen optimalen Parametern trainiert wurde, auf dem zurückgehaltenen Testdatensatz, um dessen Generalisierungsfähigkeit zu messen und die endgültige Genauigkeit zu berichten.
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
from scipy.stats import randint
import numpy as np
# Beispieldaten laden
X, y = load_iris(return_X_y=True)
# Trainings- und Testdaten splitten
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Pipeline definieren: Skalierung + Modell
pipeline = Pipeline([
('scaler', StandardScaler()),
('classifier', RandomForestClassifier(random_state=42))
])
# Suchraum für die Hyperparameter definieren
param_dist = {
'classifier__n_estimators': randint(50, 200),
'classifier__max_depth': randint(2, 10),
'classifier__min_samples_split': randint(2, 10),
'classifier__min_samples_leaf': randint(1, 5)
}
# RandomizedSearchCV konfigurieren
random_search = RandomizedSearchCV(
pipeline,
param_distributions=param_dist,
n_iter=100,
cv=10,
scoring='accuracy',
random_state=42,
n_jobs=-1
)
# Optimierung durchführen
random_search.fit(X_train, y_train)
# Bestes Modell und Score ausgeben
print("Beste Parameterkombination:")
print(random_search.best_params_)
print(f"Genauigkeit auf Testdaten: {random_search.score(X_test, y_test):.4f}")Ergebnis:
Beste Parameterkombination:
{'classifier__max_depth': 5, 'classifier__min_samples_leaf': 1, 'classifier__min_samples_split': 5, 'classifier__n_estimators': 63}
Genauigkeit auf Testdaten: 1.0000
Mit dem folgenden Code kann man noch einen Scatter-Plot des RandomizedSearchCV-Laufs erstellen.
import matplotlib.pyplot as plt
# Ergebnisse aus dem RandomizedSearchCV extrahieren
results = random_search.cv_results_
# Die mittlere Genauigkeit und die getesteten n_estimators extrahieren
mean_scores = results['mean_test_score']
n_estimators = [params['classifier__n_estimators'] for params in results['params']]
max_depths = [params['classifier__max_depth'] for params in results['params']]
# Scatterplot: Genauigkeit in Abhängigkeit von n_estimators und max_depth
plt.figure(figsize=(10, 6))
scatter = plt.scatter(n_estimators, max_depths, c=mean_scores, cmap='viridis', s=100, edgecolors='k')
plt.colorbar(scatter, label='Mean Accuracy (CV)')
plt.xlabel('n_estimators')
plt.ylabel('max_depth')
plt.title('RandomizedSearchCV Ergebnisse für RandomForest')
plt.grid(True)
plt.tight_layout()
plt.show()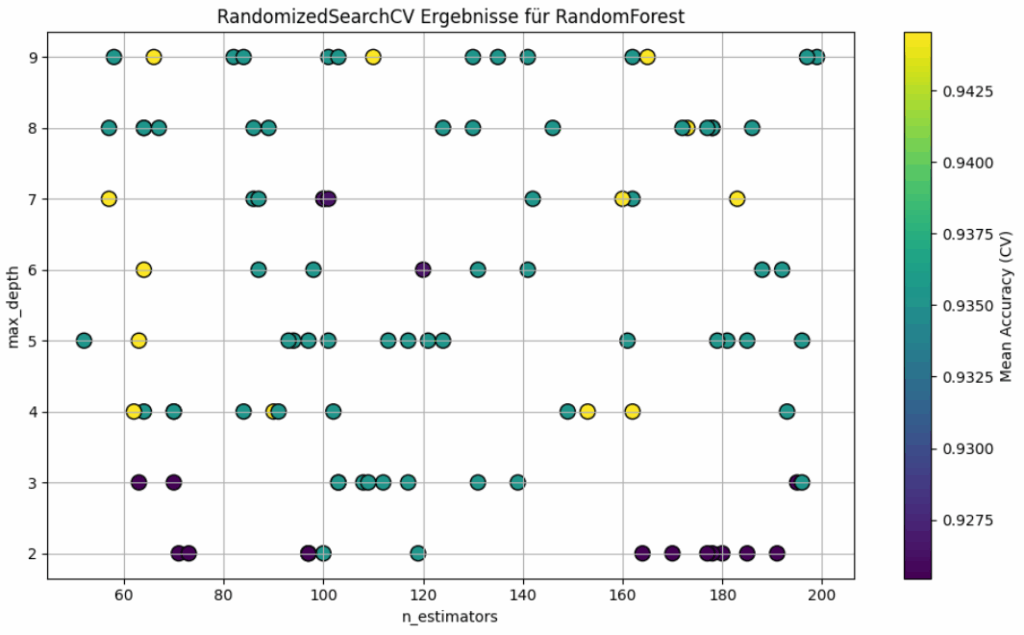
Der Scatter-Plot zeigt die Ergebnisse eines RandomizedSearchCV-Laufs für das RandomForest-Modell, bei dem zwei Hyperparameter — n_estimators (x-Achse) und max_depth (y-Achse) variiert wurden. Die Farbskala repräsentiert Mean-Genauigkeit für jede getestete Parameterkombination. Je heller der Punkt, desto besser die erreichte Genauigkeit. Die am besten getesteten Modelle liegen im Bereich der hellsten Punkte; diese sind über mehrere Kombinationen von n_estimators und max_depth verteilt, was darauf hinweist, dass das Modell relativ robust gegenüber kleineren Änderungen dieser beiden Parameter ist, solange max_depth nicht zu niedrig gewählt wird. Die Punkte mit sehr dunkler Färbung (z. B. unten bei max_depth = 2 bis 3) zeigen, dass eine zu geringer Baumtiefe die Modellleistung deutlich verschlechtert. Der Scatter-Plot zeigt keinen eindeutigen Zusammenhang zwischen n_estimators und der Genauigkeit. Viele Werte im Bereich von 60 bis 200 liefern vergleichbar gute Ergebnisse, solange die Baumtiefe ausreichend groß ist. Der Plot zeigt deutlich, dass max_depth hier der wichtige Hyperparameter ist, während n_estimators eher unwichtig ist. Dieser Scatter-Plot zeigt, dass es hilfreich ist, sich mit den Hyperparametern zu befassen, um nicht nur die beste Konfiguration zu finden, sondern auch ein Gefühl dafür zu bekommen, wie stabil und tolerant das Modell gegenüber Änderungen in den Parametern ist.
Wenn man es ganz Fancy haben möchte, kann man sich die Ergebnisse mit dem folgenden Code auch als 3D-Plot anzeigen lassen.
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # Für 3D-Plot
import numpy as np
# Zusätzlichen Parameter extrahieren
min_samples_split = [params['classifier__min_samples_split'] for params in results['params']]
# 3D-Plot vorbereiten
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
# Farbwerte basieren auf der mittleren CV-Genauigkeit
sc = ax.scatter(
n_estimators,
max_depths,
min_samples_split,
c=mean_scores,
cmap='viridis',
s=80,
edgecolor='k'
)
# Achsenbeschriftungen und Farbskala
ax.set_xlabel('n_estimators')
ax.set_ylabel('max_depth')
ax.set_zlabel('min_samples_split')
fig.colorbar(sc, ax=ax, label='Mean Accuracy (CV)')
ax.set_title('3D-Visualisierung der RandomizedSearchCV-Ergebnisse')
plt.tight_layout()
plt.show()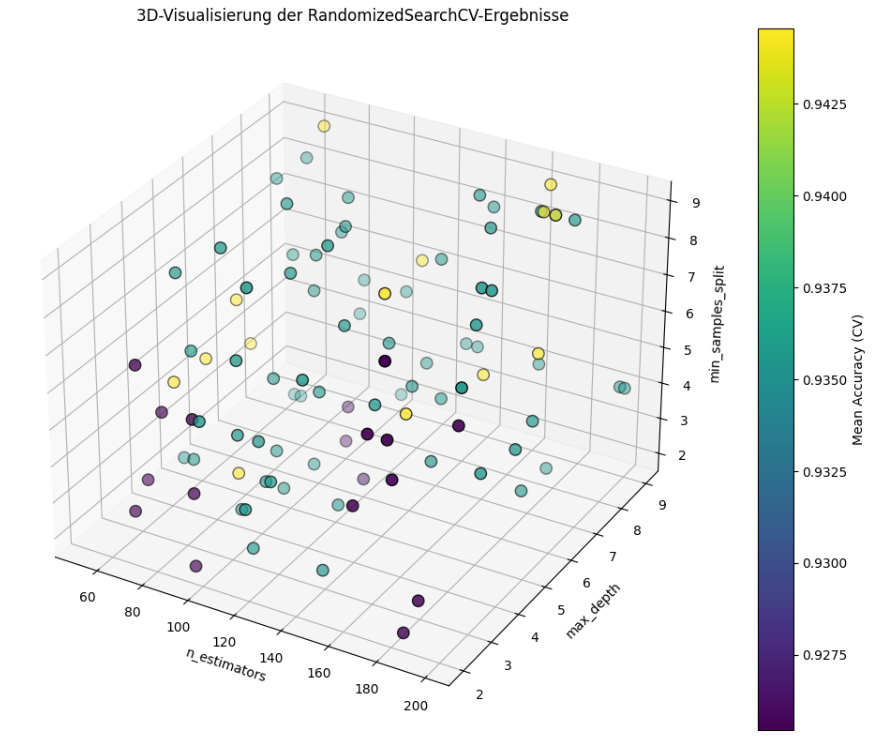
Der Plot zeigt die dreidimensionale Struktur deines Hyperparameter-Suchraums. Man erkennt direkt, welche Kombinationen zu besseren Scores führen – und wo sich die „Hotspots“ befinden, also Konfigurationen mit hoher Modellgüte. Ich persönlich bevorzuge aber die 2D-Version.
Wenn man lieber die Parameter getrennt betrachten möchte, kann man mit das folgende Skript verwenden. Es erzeugt für jeden Parameter ein zeigt den Einfluss des Parameters auf die Accuracy.
import matplotlib.pyplot as plt
import numpy as np
# Annahme: Diese Variablen existieren bereits aus dem RandomizedSearchCV
# n_estimators, max_depths, min_samples_split, mean_scores
# Sicherheitshalber in Arrays umwandeln
n_estimators_arr = np.array(n_estimators)
max_depths_arr = np.array(max_depths)
min_samples_split_arr = np.array(min_samples_split)
mean_scores_arr = np.array(mean_scores)
# Plot-Stil (optional)
plt.style.use('seaborn-v0_8-darkgrid')
# Subplots erstellen
fig, axs = plt.subplots(1, 3, figsize=(18, 5))
# 1. Plot: n_estimators vs. mean_scores
axs[0].scatter(n_estimators_arr, mean_scores_arr, c=mean_scores_arr, cmap='viridis', edgecolor='k')
axs[0].set_xlabel('n_estimators')
axs[0].set_ylabel('Mean Accuracy (CV)')
axs[0].set_title('Einfluss von n_estimators')
# 2. Plot: max_depth vs. mean_scores
axs[1].scatter(max_depths_arr, mean_scores_arr, c=mean_scores_arr, cmap='viridis', edgecolor='k')
axs[1].set_xlabel('max_depth')
axs[1].set_ylabel('Mean Accuracy (CV)')
axs[1].set_title('Einfluss von max_depth')
# 3. Plot: min_samples_split vs. mean_scores
axs[2].scatter(min_samples_split_arr, mean_scores_arr, c=mean_scores_arr, cmap='viridis', edgecolor='k')
axs[2].set_xlabel('min_samples_split')
axs[2].set_ylabel('Mean Accuracy (CV)')
axs[2].set_title('Einfluss von min_samples_split')
# Layout optimieren und anzeigen
plt.tight_layout()
plt.show()Das Ergebnis sieht dann wie folgt aus:
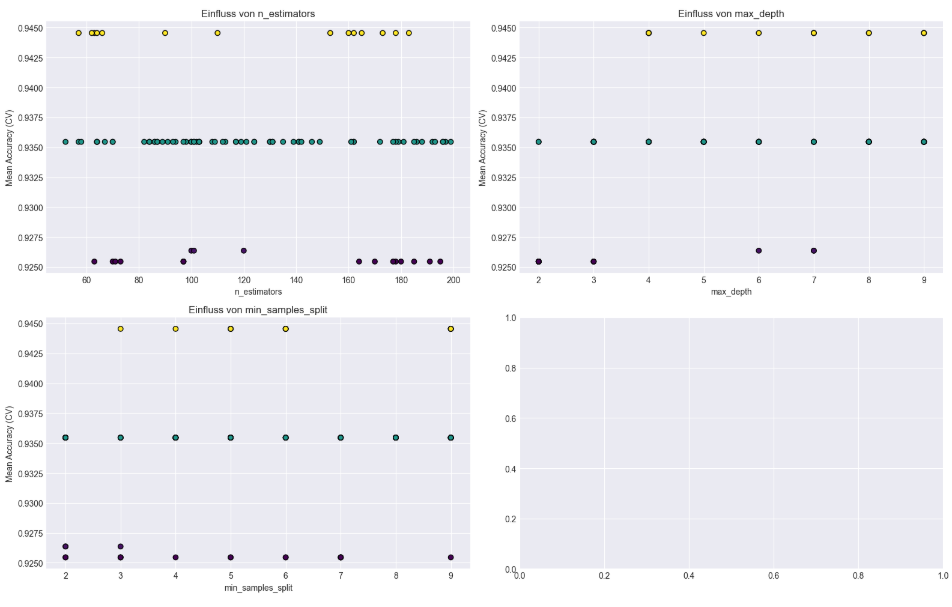
Das Bild zeigt drei Scatterplots, die jeweils den Einfluss eines Hyperparameters auf die mittlere Cross-Validation-Genauigkeit (Mean Accuracy (CV)).
Einfluss von n_estimators (oben links)
Die Punktwolke zeigt, dass die Genauigkeit relativ robust gegenüber der Anzahl der Bäume ist. Es gibt keine klare lineare Beziehung: Sowohl bei niedrigen (z. B. 60) als auch bei höheren Werten (bis 200) sind gute und schlechte Scores vertreten. Ein Plateau bei ~0.935 ist deutlich sichtbar, was auf eine häufige mittlere Leistung hindeutet. Werte bei 60 und170 scheinen besonders viele gute Resultate zu bringen.
Einfluss von max_depth (oben rechts)
Hier ist der Effekt deutlicher: Werte unterhalb von 4 führen häufig zu schlechteren Ergebnissen. Ab einer Tiefe von ca. 5 oder mehr erreichen viele Konfigurationen die höchsten Genauigkeitswerte. Der Plot zeigt also, dass ein zu geringer max_depth die Modellleistung deutlich einschränkt.
Einfluss von min_samples_split (unten links)
Auch hier sind drei Leistungsgruppen erkennbar. Unten (~0.925), im Mittelfeld (~0.935) und oben (~0.945). Sehr kleine Werte (2, 3) führen sowohl zu guten als auch schlechten Scores – sie sind riskanter. Höhere Werte (z. B. 9) schneiden ebenfalls gut ab – evtl. weil sie Überanpassung verhindern.
Das Modell ist nicht extrem sensitiv gegenüber n_estimators, reagiert aber empfindlicher auf max_depth und min_samples_split. Eine zu kleine Tiefe oder ein zu kleiner Split-Wert kann die Leistung spürbar verschlechtern. Interessanterweise gibt es mehrere Kombinationen, die ein ähnliches Top-Ergebnis bringen – das spricht für eine gewisse Robustheit im Parameterraum.
