TODO für Tag 23
- Unterschied zu einfacher LinearRegression
- Einfluss von Regularisierung verstehen
Unterschied zu einfacher LinearRegression
Die einfache LinearRegression in scikit-learn versucht, eine Gerade oder Hyperebene zu finden, die die Summe der quadrierten Abweichungen zwischen den vorhergesagten und den tatsächlichen Werten minimiert. Sie ist anfällig für Overfitting, besonders bei vielen Features oder wenn Features stark miteinander korrelieren, was zu instabilen Koeffizienten führen kann.
Ridge-Regression fügt der Kostenfunktion der einfachen linearen Regression einen zusätzlichen Term hinzu. Dieser Term ist die Summe der quadrierten Werte aller Koeffizienten, multipliziert mit einem Regularisierungsparameter namens alpha. Durch diese sogenannte L2-Regularisierung werden die Koeffizienten dazu gezwungen, kleiner zu werden. Sie werden zwar in Richtung 0 geschrumpft, erreichen aber selten exakt 0. Das Ergebnis ist ein Modell, das robuster gegenüber kleinen Änderungen in den Trainingsdaten ist und eine geringere Varianz aufweist.
Beispiel
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
# Daten generieren
np.random.seed(42) # Für Reproduzierbarkeit
n_samples = 50
X = np.sort(np.random.rand(n_samples)) * 10 # X-Werte zwischen 0 und 10
y_true = 2 * X - 5 + np.random.randn(n_samples) * 2 # Wahre Beziehung mit Rauschen: y = 2x - 5
X_reshaped = X[:, np.newaxis]
# Modelle definieren und trainieren
# Einfache Lineare Regression (mit polynomialen Features, um Overfitting
# zu provozieren)
# Pipeline: PolynomialFeatures -> StandardScaler -> LinearRegression
poly_degree = 10 # Hoher Grad, um Overfitting zu ermöglichen
linear_model_poly = make_pipeline(
PolynomialFeatures(degree=poly_degree, include_bias=False),
StandardScaler(), # Skalierung ist gut für regularisierte Modelle
LinearRegression()
)
linear_model_poly.fit(X_reshaped, y_true)
# Ridge Regression (mit denselben polynomialen Features)
# Der Alpha-Parameter steuert die Stärke der Regularisierung.
# Ein kleineres Alpha bedeutet weniger Regularisierung, ein größeres Alpha mehr.
ridge_model_poly = make_pipeline(
PolynomialFeatures(degree=poly_degree, include_bias=False),
StandardScaler(),
Ridge(alpha=1.0) # Alternativ: alpha=0.1 oder alpha=10.0
)
ridge_model_poly.fit(X_reshaped, y_true)
# Um die Linien zu zeichnen, wird ein Satz von X-Werten benötigt
X_plot = np.linspace(X.min(), X.max(), 200)[:, np.newaxis]
# Vorhersagen für die Visualisierung
y_linear_poly_pred = linear_model_poly.predict(X_plot)
y_ridge_poly_pred = ridge_model_poly.predict(X_plot)
# Ergebnisse visualisieren
plt.figure(figsize=(12, 7))
plt.scatter(X, y_true, color='skyblue', label='Ursprüngliche Datenpunkte', alpha=0.7, edgecolor='k')
plt.plot(X_plot, y_linear_poly_pred, color='red', linewidth=2, label=f'Lineare Regression (Grad {poly_degree}) - Overfitting')
plt.plot(X_plot, y_ridge_poly_pred, color='green', linewidth=2, linestyle='--', label=f'Ridge Regression (Grad {poly_degree}, alpha=1.0)')
# Optional: Plotten der "wahren" Funktion, wenn bekannt (hier y = 2x - 5)
# y_true_line = 2 * X_plot.ravel() - 5
# plt.plot(X_plot, y_true_line, color='gray', linestyle=':', linewidth=2, label='Wahre Funktion (y=2x-5)')
plt.xlabel("Feature X")
plt.ylabel("Zielvariable y")
plt.title("Vergleich: Lineare Regression vs. Ridge Regression mit polynomialen Features")
plt.legend()
plt.grid(True)
plt.ylim(y_true.min() - 5, y_true.max() + 5) # Achsenlimits anpassen für bessere Sichtbarkeit
plt.show()
# Koeffizienten vergleichen (optional)
# Wir müssen auf den Regressionsschritt in der Pipeline zugreifen
coeffs_linear = linear_model_poly.named_steps['linearregression'].coef_
coeffs_ridge = ridge_model_poly.named_steps['ridge'].coef_
print(f"Anzahl der Koeffizienten: {len(coeffs_linear)}")
print(f"Maximale absolute Koeffizienten Linear: {np.max(np.abs(coeffs_linear)):.2f}")
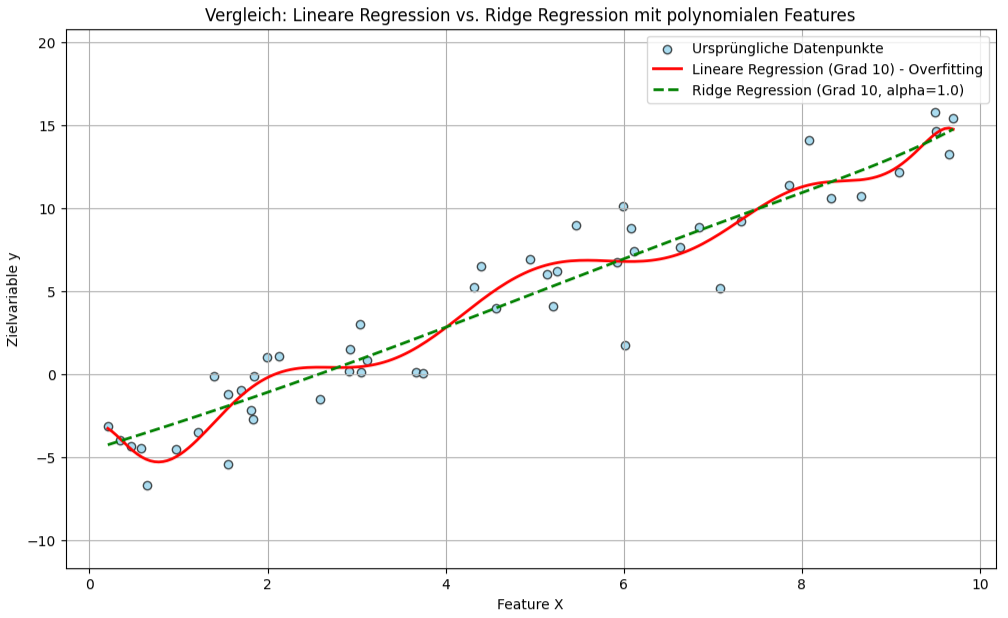
print(f"Maximale absolute Koeffizienten Ridge: {np.max(np.abs(coeffs_ridge)):.2f}")In dem Beispiel werden zunächst Datenpunkte, die einer linearen Beziehung mit etwas Rauschen folgen. Um den Effekt der Regularisierung deutlich zu machen, wird PolynomialFeatures mit einem hohen Grad verwendet. Dies führt dazu, dass die einfache LinearRegression versucht, sich sehr eng an die Trainingsdaten anzupassen, einschließlich des Rauschens, was zu einer stark oszillierenden Kurve und somit zu Overfitting führt. Man sieht, dass die rote Linie (einfache Regression) versucht, jeden Punkt zu „fangen“ und dadurch sehr instabil wird.
Die Ridge-Regression hingegen fügt einen Strafterm für die Größe der Koeffizienten hinzu. Dies zwingt die Koeffizienten, kleiner zu bleiben. Das Ergebnis ist die grüne, gestrichelte Linie. Sie folgt dem allgemeinen Trend der Daten immer noch gut, ist aber deutlich glatter und weniger anfällig für die Ausreißer und das Rauschen in den Trainingsdaten.
Der Parameter alpha in Ridge(alpha=1.0) steuert die Stärke dieser Regularisierung. Ein alpha von 0 würde die Ridge-Regression in eine einfache lineare Regression ohne Regularisierung zurückführen. Ein sehr großes alpha würde alle Koeffizienten stark gegen Null drücken, was zu Underfitting führen könnte, bei der das Modell selbst den grundlegenden Trend nicht mehr erfasst.
Die Ausgabe der Koeffizienten am Ende zeigt typischerweise, dass die absoluten Werte der Koeffizienten bei der Ridge-Regression kleiner sind als bei der einfachen linearen Regression, besonders wenn Overfitting bei letzterer auftritt. Dies ist ein direktes Ergebnis der L2-Regularisierung, die große Koeffizienten „bestraft“. Die Skalierung der Features mit StandardScaler ist hierbei eine gute Praxis, da Regularisierungsmethoden empfindlich auf die Skala der Eingabefeatures reagieren.
Wie man in dem Plot sieht, generalisiert Ridge-Regression ganz gut.
Anzahl der Koeffizienten: 10
Maximale absolute Koeffizienten Linear: 1356714.36
Maximale absolute Koeffizienten Ridge: 4.68
Das Diagramm visualisiert den Vergleich zwischen einer einfachen polynomialen Regression und einer Ridge-Regression anhand der verrauschten Datenpunkten. Die rote, durchgezogene Linie repräsentiert eine Lineare Regression, die deutlich überangepasst ist. Sie schwankt stark und versucht, sich eng an jeden Datenpunkt, inklusive des Rauschens, anzulegen. Im Gegensatz dazu zeigt die grüne, gestrichelte Linie die Ridge-Regression mit demselben polynomialen Grad und einem Alpha-Wert von 1.0. Diese Linie verläuft wesentlich glatter und fängt den allgemeinen Trend der Daten ein, ohne von einzelnen Ausreißern oder dem Rauschen stark beeinflusst zu werden, was die regularisierende Wirkung von Ridge verdeutlicht.
Lasso-Regression
Die Lasso-Regression verfolgt einen ähnlichen Ansatz, verwendet aber eine andere Art von Strafterm. Statt der Summe der quadrierten Koeffizienten wird hier die Summe der Absolutbeträge der Koeffizienten zur Kostenfunktion addiert, ebenfalls multipliziert mit alpha. Diese L1-Regularisierung hat die Eigenschaft, dass sie einige Koeffizienten exakt auf 0 setzen kann. Dadurch führt Lasso nicht nur eine Regularisierung durch, sondern betreibt gleichzeitig auch eine automatische Merkmalsauswahl, da Features mit einem Koeffizienten von 0 effektiv aus dem Modell entfernt werden.Lasso-Regression
Hier ein Beispiel, das Lasso-Regression anstelle von Ridge-Regression verwendet:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, Lasso
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.exceptions import ConvergenceWarning
import warnings
# Konvergenzwarnungen von Lasso unterdrücken, wenn alpha sehr klein ist oder max_iter nicht reicht
# Für dieses Beispiel ist es oft ok, aber in der Praxis sollte man dies untersuchen.
warnings.filterwarnings("ignore", category=ConvergenceWarning)
# Daten generieren
np.random.seed(42) # Für Reproduzierbarkeit
n_samples = 50
X = np.sort(np.random.rand(n_samples)) * 10 # X-Werte zwischen 0 und 10
y_true = 2 * X - 5 + np.random.randn(n_samples) * 2 # Wahre Beziehung mit Rauschen: y = 2x - 5
# Transformation von X in ein 2D-Array für scikit-learn
X_reshaped = X[:, np.newaxis]
# Modelle definieren und trainieren
# Einfache Lineare Regression (mit polynomialen Features, um Overfitting zu provozieren)
poly_degree = 10 # Hoher Grad, um Overfitting zu ermöglichen
linear_model_poly = make_pipeline(
PolynomialFeatures(degree=poly_degree, include_bias=False),
StandardScaler(), # Skalierung ist gut für regularisierte Modelle
LinearRegression()
)
linear_model_poly.fit(X_reshaped, y_true)
# Lasso Regression (mit denselben polynomialen Features)
# Der Alpha-Parameter steuert die Stärke der Regularisierung.
# Lasso kann empfindlicher auf alpha reagieren. Ein kleineres Alpha ist oft nötig.
# max_iter wird erhöht, da Lasso manchmal mehr Iterationen zur Konvergenz benötigt.
lasso_alpha = 0.1
lasso_model_poly = make_pipeline(
PolynomialFeatures(degree=poly_degree, include_bias=False),
StandardScaler(),
Lasso(alpha=lasso_alpha, max_iter=10000, tol=0.01)
)
lasso_model_poly.fit(X_reshaped, y_true)
X_plot = np.linspace(X.min(), X.max(), 200)[:, np.newaxis]
# Vorhersagen für die Visualisierung
y_linear_poly_pred = linear_model_poly.predict(X_plot)
y_lasso_poly_pred = lasso_model_poly.predict(X_plot)
# Ergebnisse visualisieren
plt.figure(figsize=(12, 7))
plt.scatter(X, y_true, color='skyblue', label='Ursprüngliche Datenpunkte', alpha=0.7, edgecolor='k')
plt.plot(X_plot, y_linear_poly_pred, color='red', linewidth=2, label=f'Lineare Regression (Grad {poly_degree}) - Overfitting')
plt.plot(X_plot, y_lasso_poly_pred, color='purple', linewidth=2, linestyle='-.', label=f'Lasso Regression (Grad {poly_degree}, alpha={lasso_alpha})')
plt.xlabel("Feature X")
plt.ylabel("Zielvariable y")
plt.title("Vergleich: Lineare Regression vs. Lasso Regression mit polynomialen Features")
plt.legend()
plt.grid(True)
plt.ylim(y_true.min() - 5, y_true.max() + 5) # Achsenlimits anpassen für bessere Sichtbarkeit
plt.show()
# Koeffizienten vergleichen
coeffs_linear = linear_model_poly.named_steps['linearregression'].coef_
coeffs_lasso = lasso_model_poly.named_steps['lasso'].coef_
print(f"Anzahl der Koeffizienten insgesamt: {len(coeffs_linear)}")
print(f"Koeffizienten Lineare Regression (Auszug der ersten 5): {np.round(coeffs_linear[:5], 2)}")
print(f"Koeffizienten Lasso Regression (Auszug der ersten 5): {np.round(coeffs_lasso[:5], 2)}")
print(f"Anzahl der Koeffizienten, die von Lasso auf Null gesetzt wurden: {np.sum(coeffs_lasso == 0)} von {len(coeffs_lasso)}")
print(f"Maximale absolute Koeffizienten Linear: {np.max(np.abs(coeffs_linear)):.2f}")
print(f"Maximale absolute Koeffizienten Lasso: {np.max(np.abs(coeffs_lasso)):.2f}")Der Code generiert zunächst synthetische Daten, indem 50 sortierte X-Werte zwischen 0 und 10 erzeugt und zugehörige Y-Werte auf Basis einer linearen Grundbeziehung (y = 2x – 5) mit hinzugefügtem normalverteiltem Rauschen berechnet werden. Um das Verhalten bei potenzieller Überanpassung zu demonstrieren und den Effekt von Lasso zu zeigen, werden diese X-Werte anschließend in polynomiale Merkmale bis zum Grad 10 transformiert. Eine erste Pipeline, bestehend aus dieser Merkmalserzeugung, einer StandardScaler-Skalierung zur Normierung der Daten und einer einfachen LinearRegression, wird auf diesen transformierten Daten trainiert, um als Referenz für Überanpassung zu dienen. Parallel dazu wird eine zweite Pipeline mit den identischen polynomialen Merkmalen und der Skalierung erstellt, die jedoch anstelle der einfachen linearen Regression ein Lasso-Modell mit einem Regularisierungsparameter alpha von 0.1, einer erhöhten maximalen Iterationszahl von 10000 (max_iter) und einer spezifischen Toleranz (tol) von 0.01 verwendet und ebenfalls auf den Daten trainiert, um dessen regularisierende und merkmalsselektierende Eigenschaften zu demonstrieren.
Ausgabe:
Anzahl der Koeffizienten insgesamt: 10
Koeffizienten Lineare Regression (Auszug der ersten 5): [ 2.3430000e+01 -1.3194900e+03 1.8990960e+04 -1.2454123e+05
4.5493289e+05]
Koeffizienten Lasso Regression (Auszug der ersten 5): [5.72 0. 0. 0. 0. ]
Anzahl der Koeffizienten, die von Lasso auf Null gesetzt wurden: 9 von 10
Maximale absolute Koeffizienten Linear: 1356714.36
Maximale absolute Koeffizienten Lasso: 5.72
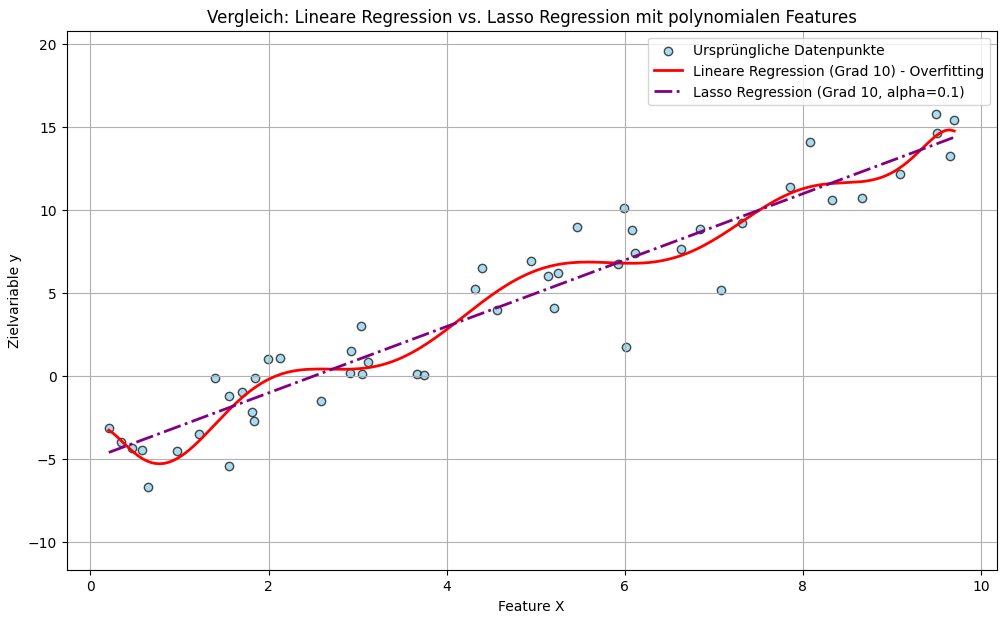
Das Bild zeigt den Vergleich der Anpassungsgüte einer einfachen linearen Regression und einer Lasso-Regression an einen Satz verrauschter Datenpunkte. Die durchgezogene rote Linie, welche die einfache lineare Regression repräsentiert, zeigt ein starkes Überanpassungsverhalten, indem sie oszilliert und versucht, sich eng an die einzelnen, auch verrauschten, Datenpunkte anzulegen. Im Gegensatz dazu verläuft die blau gestrichelte Linie der Lasso-Regression deutlich glatter und fängt den allgemeinen Trend der Daten ein, ohne von Ausreißern oder dem Rauschen übermäßig beeinflusst zu werden, was die regularisierende Wirkung von Lasso verdeutlicht.
Die Ausgabe „Anzahl der Koeffizienten, die von Lasso auf Null gesetzt wurden: 9 von 10“ bedeutet, dass das Lasso-Regressionsmodell von den 10 ihm zur Verfügung gestellten Features entschieden hat, dass nur eines davon wichtig ist. Die anderen 9 Merkmale wurden als irrelevant oder redundant eingestuft und ihre zugehörigen Gewichte wurden auf exakt 0 reduziert.
Dies ist das Kernmerkmal und der Hauptvorteil der Lasso-Regression: Sie führt eine automatische Merkmalsauswahl (Feature Selection) durch und vereinfacht das Modell drastisch.
Die „wahren“ Daten werden mit einer sehr einfachen, linearen Formel erzeugt: y = 2x – 5 plus etwas zufälliges Rauschen. Ein einfaches lineares Modell wäre also ideal, um diesen Zusammenhang zu beschreiben.
Das Skript verwendet PolynomialFeatures(degree=10). Das bedeutet, es nimmt das eine ursprüngliche Merkmal X und erzeugt daraus 10 neue Merkmale: X¹, X², X³, …, X¹⁰. Das Modell hat nun also 10 Koeffizienten, an denen es drehen kann, um die Daten zu beschreiben.
Lasso hat die Ziele die vorhandene Trainingsdaten gut zu beschreiben (wie die lineare Regression). Die Summe der absoluten Werte aller Koeffizienten so klein wie möglich zu halten. Dieser zweite Punkt ist die sogenannte L1-Regularisierung (gesteuert durch den alpha-Parameter). Die te L1-Regularisierung dient als „Strafe“ für Komplexität. Das Modell muss abwägen: „Lohnt es sich, diesen Koeffizienten ungleich 0 zu machen, um die Daten ein kleines bisschen besser zu fitten, oder ist die Strafe dafür zu hoch?“ Da der wahre Zusammenhang in den Daten linear ist (also am besten durch X¹ beschrieben wird), stellt Lasso fest, dass Der Koeffizient für X¹ ist sehr nützlich, um den generellen Trend zu erfassen. Es lohnt sich, die „Strafe“ für diesen einen Koeffizienten in Kauf zu nehmen und die Koeffizienten für X², X³, X⁴ etc. helfen nur dabei, das zufällige Rauschen zu modellieren, tragen aber nicht wesentlich zum Verständnis des wahren Musters bei. Der geringe Gewinn bei der Anpassung an die Daten rechtfertigt die Strafe nicht. Lasso setzt also die Koeffizienten für die 9 „nutzlosen“ höhergradigen Merkmale auf exakt 0. Es behält nur den einen Koeffizienten für das wichtigste Merkmal (X¹) bei.
Die Ausgabe „9 von 10 Koeffizienten auf Null gesetzt“ ist also der Beweis dafür, dass Lasso erfolgreich war:
- Es hat das übermäßig komplexe Modell mit 10 Merkmalen „ausgedünnt“.
- Es hat automatisch das eine Merkmal ausgewählt, das wirklich zählt.
- Es hat ein viel einfacheres Modell geschaffen, das dem wahren Zusammenhang viel näher kommt und besser auf neue, unbekannte Daten generalisieren würde.
Vergleich von Ridge und Lasso
Der wesentliche Unterschied zur einfachen LinearRegression liegt also darin, dass sowohl Ridge als auch Lasso eine Strafe auf die Größe der Koeffizienten erheben, um Überanpassung zu vermeiden und die Modellstabilität zu verbessern. LinearRegression tut dies nicht und optimiert ausschließlich die Fehlerquadratsumme. Ridge schrumpft Koeffizienten durch eine L2-Strafe, während Lasso dies durch eine L1-Strafe tut und dabei zur Merkmalsauswahl neigt. Die Stärke der Regularisierung wird bei beiden durch den Parameter alpha gesteuert: ein höheres alpha bedeutet stärkere Regularisierung und kleinere Koeffizienten.
L1-Strafe und L2-Strafe
Die L1-Strafe und die L2-Strafe sind Regularisierungstechniken, die in Machine-Learning-Modellen wie der linearen Regression verwendet werden, um Overfitting zu verhindern und die Generalisierungsfähigkeit des Modells zu verbessern.
Die L2-Strafe, auch bekannt als Ridge-Regularisierung, fügt der Verlustfunktion die Summe der quadrierten Werte aller Koeffizienten hinzu, multipliziert mit einem Regularisierungsparameter (Alpha). Dieser Term zwingt die Koeffizienten dazu, kleiner zu werden. Da die Quadrate der Koeffizienten verwendet werden, werden sehr große Koeffizienten besonders stark bestraft. Die L2-Strafe schrumpft die Koeffizienten zwar in Richtung 0, setzt sie aber typischerweise nicht exakt auf 0, es sei denn, ein Feature ist absolut irrelevant und Alpha sehr hoch. Die L2-Strafe ist nützlich, um die Stabilität des Modells zu erhöhen, besonders wenn viele Merkmale miteinander korrelieren.
Die L1-Strafe, bekannt als Lasso-Regularisierung, fügt stattdessen die Summe der Absolutbeträge aller Koeffizienten zur Verlustfunktion hinzu, ebenfalls multipliziert mit einem Regularisierungsparameter. Der entscheidende Unterschied zur L2-Strafe besteht darin, dass die L1-Strafe dazu neigt, einige Koeffizienten exakt auf 0 zu setzen. Dies führt zu einer automatischen Merkmalsauswahl, da Merkmale mit einem Koeffizienten von 0 effektiv aus dem Modell entfernt werden. Lasso ist daher besonders nützlich, wenn man vermutet, dass viele der vorhandenen Features für die Vorhersage irrelevant sind und man ein einfacheres, interpretierbareres Modell erhalten möchte.
Zusammenfassend lässt sich sagen, dass beide Strafen darauf abzielen, die Komplexität des Modells zu reduzieren, indem sie große Koeffizienten bestrafen. Die L2-Strafe führt zu kleineren, aber meist von Null verschiedenen Koeffizienten, während die L1-Strafe eine inhärente Merkmalsauswahl durchführt, indem sie einige Koeffizienten exakt auf 0 setzt. Die Stärke der Regularisierung wird bei beiden durch den jeweiligen Regularisierungsparameter gesteuert.
Einfluss von Regularisierung verstehen
In den Beispielen demonstriert die einfache LinearRegression eine deutliche Überanpassung. Dies äußert sich in einer stark oszillierenden Kurve (rote Linie), die versucht, jeden Datenpunkt exakt zu treffen. Das resultiert oft in extrem großen, instabilen Koeffizienten.
Der Einfluss der Ridge-Regression besteht darin, diese Überanpassung durch die L2-Strafe zu mildern. Sie zwingt die Koeffizienten, kleiner zu werden, was zu einer wesentlich glatteren Kurve führt, die den allgemeinen Trend der Daten besser erfasst, ohne jedem Rauschpunkt zu folgen. Die Koeffizienten werden zwar reduziert, aber typischerweise nicht exakt auf 0 gesetzt.
Die Lasso-Regression zeigt einen ähnlichen glättenden Effekt durch die L1-Strafe. Ihr besonderer Einfluss liegt jedoch darin, dass sie einige der polynomialen Koeffizienten exakt auf 0 setzen kann. Dies führt zu einer automatischen Feature-Auswahl, bei der die weniger wichtigen polynomialen Terme effektiv aus dem Modell entfernt werden, was zu einem potenziell einfacheren Modell führt, was das Overfitting reduziert.
Beide Regularisierungsmethoden helfen also, robustere Modelle zu erstellen, die besser generalisieren.
