TODO Für Tag 14
- Unterschied zwischen StandardScaler, MinMaxScaler
- Wann ist Skalierung unbedingt notwendig?
Unterschied zwischen StandardScaler, MinMaxScaler
In scikit-learn gibt es sowohl den StandardScaler als auch den MinMaxScaler zur Skalierung von numerischen Features. Beide sind Werkzeuge zur Vorverarbeitung von Daten für Machine-Learning-Modelle, da viele Algorithmen empfindlich auf die Skalierung der Features reagieren. Der StandardScaler skaliert die Daten so, dass sie einen Mittelwert von 0 und eine Standardabweichung von 1 aufweisen. Im Gegensatz dazu skaliert der MinMaxScaler die Features auf einen vorgegebenen Bereich, indem er die Min- und Max-Werte des Features verwendet. Dies stellt sicher, dass alle Werte innerhalb dieses Bereichs liegen. Die Wahl zwischen beiden hängt oft vom spezifischen Algorithmus und der Natur der Daten ab.
Beispiel: StandardScaler in Aktion
from sklearn.preprocessing import StandardScaler
import numpy as np
# Beispiel-Daten (z. B. zwei Features mit jeweils 3 Samples)
X = np.array([
[1.0, 200.0],
[2.0, 300.0],
[3.0, 400.0]
])
# StandardScaler initialisieren
scaler = StandardScaler()
# Fit und Transformation der Daten
X_scaled = scaler.fit_transform(X)
print("Originaldaten:\n", X)
print("\nStandardisierte Daten:\n", X_scaled)
print("\nMittelwerte:\n", scaler.mean_)
print("\nStandardabweichungen:\n", scaler.scale_)Ausgabe:
Originaldaten:
[[ 1. 200.]
[ 2. 300.]
[ 3. 400.]]
Standardisierte Daten:
[[-1.22474487 -1.22474487]
[ 0. 0. ]
[ 1.22474487 1.22474487]]
Mittelwerte:
[ 2. 300.]
Standardabweichungen:
[ 0.81649658 81.64965809]In den Originaldaten gibt es 2 Features:
- Feature 1: 1, 2, 3
- Feature 2: 200, 300, 400
Der Mittelwert wird spaltenweise berechnet:
- Feature 1:
(1+2+3)/3=2(1+2+3)/3 = 2(1+2+3)/3=2 - Feature 2:
(200+300+400)/3=300(200+300+400)/3 = 300(200+300+400)/3=300
Die Standardabweichung wird ebenfalls spaltenweise berechnet:

Die standardisierten Daten sind dann:
-1.22474487 -1.22474487
0. 0.
1.22474487 1.22474487
Beide Features wurden unabhängig voneinander so transformiert. Die Struktur der Daten bleibt erhalten, aber die Skala ist normiert. Damit sind die Daten nun besser geeignet für Algorithmen, die sensibel auf Skalenunterschiede reagieren (z. B. PCA, SVM, kNN).
Mit dem folgenden Plot kann man die Daten noch mal grafisch darstellen.
# Plot: Original vs. Standardisiert
plt.figure(figsize=(10, 5))
# Originaldaten plotten
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], color='blue', label='Originaldaten')
plt.title("Originaldaten")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.grid(True)
plt.legend()
# Standardisierte Daten plotten
plt.subplot(1, 2, 2)
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], color='green', label='Standardisierte Daten')
plt.axhline(0, color='gray', linestyle='--')
plt.axvline(0, color='gray', linestyle='--')
plt.title("Nach StandardScaler")
plt.xlabel("Feature 1 (z)")
plt.ylabel("Feature 2 (z)")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()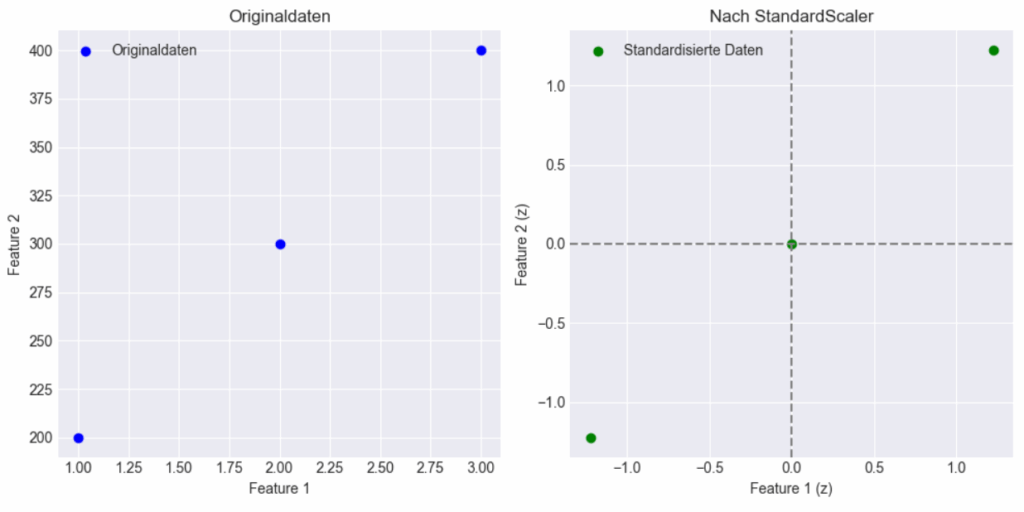
Links sieht man die Originaldaten im Rohzustand. Feature 1 reicht von 1–3, Feature 2 von 200–400. Rechts die standardisierten Daten. Mittelwert wurde auf (0, 0) verschoben und die Achsen wurden gestreckt/gestaucht, sodass beide Features eine Standardabweichung von 1 haben. Die Form bleibt erhalten. Der Plot zeigt, dass der StandardScaler die Form der Verteilung nicht zerstört, sondern nur Skalierung und Zentrierung vornimmt.
Wichtig: Eine Standardabweichung von 1 bedeutet nicht, dass die Werte zwischen -1 und +1 liegen. Es bedeutet: Der durchschnittliche Abstand der Daten zum Mittelwert beträgt 1. Dass die standardisierten Werte bei ±1.2247 enden, liegt daran, dass das der Abstand der Randwerte vom Mittelwert in Einheiten der Standardabweichung ist. Die Verteilung ist also korrekt skaliert – auch wenn die Werte nicht exakt zwischen -1 und +1 liegen.
Hier noch mal ein Beispiel mit einem größeren Datensatz, der das Verhalten der Standardabweichung besser wiedergeben kann.
Beispiel mit Visualisierung:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
# Seed für Reproduzierbarkeit
np.random.seed(42)
# Simuliere 1000 normalverteilte Werte mit Mittelwert 100, Standardabweichung 15
X = np.random.normal(loc=100, scale=15, size=(1000, 1))
# Wende StandardScaler an
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Daten in 1D extrahieren
X_scaled_flat = X_scaled.flatten()
# Plot der Verteilung nach dem Scaling
plt.figure(figsize=(10, 5))
plt.hist(X_scaled_flat, bins=50, color='skyblue', edgecolor='black', alpha=0.7, density=True)
plt.title("Histogramm der standardisierten Daten (n = 1000)")
plt.xlabel("Standardisierte Werte (z)")
plt.ylabel("Dichte")
# Standardabweichungslinien (±1σ, ±2σ, ±3σ)
for i in range(1, 4):
plt.axvline(x=+i, color='red', linestyle='--', label=f'+{i}σ' if i == 1 else None)
plt.axvline(x=-i, color='red', linestyle='--', label=f'-{i}σ' if i == 1 else None)
# Legende nur einmal einzeichnen
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()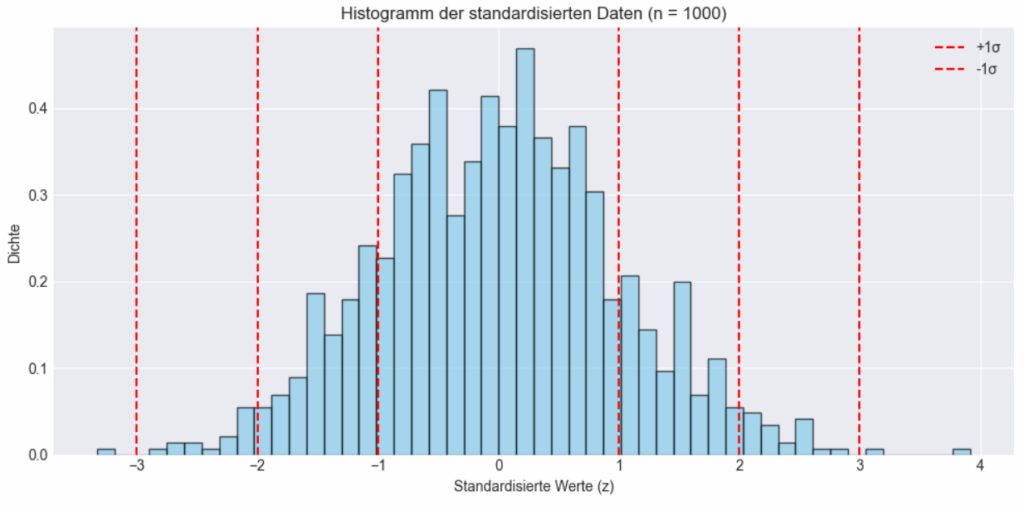
Das Histogramm zeigt die Verteilung standardisierter Daten mit einem Mittelwert von 0 und einer Standardabweichung von 1. Die rote gestrichelte Linie markiert jeweils die Abstände von einer, zwei und drei Standardabweichungen vom Mittelwert nach links und rechts. Das Histogramm zeigt deutlich, dass der Großteil der Daten innerhalb des Bereichs von -1 bis +1 Standardabweichung liegt. Dies bestätigt das statistische Prinzip, dass bei einer Normalverteilung etwa 68 % der Werte in diesem Bereich liegen. Mit zunehmender Entfernung vom Zentrum nimmt die Häufigkeit deutlich ab, was die typische Glockenform einer Normalverteilung widerspiegelt. Die Daten außerhalb der Bereiche ±2σ und ±3σ treten seltener auf und belegen anschaulich, wie selten extreme Abweichungen in standardisierten, normalverteilten Daten vorkommen.
Der MinMaxScaler skaliert Daten, indem er sie in einen definierten Wertebereich, z.B. zwischen 0 und 1, transformiert, wobei der kleinste Wert einer Feature-Spalte auf 0 und der größte auf 1 gesetzt wird. Dies geschieht durch eine lineare Transformation, die die relative Verteilung der Werte beibehält, aber deren absoluten Wertebereich anpasst. Während der MinMaxScaler empfindlicher auf Ausreißer reagiert, da Extremwerte die Skalierung stark beeinflussen, ist der StandardScaler robuster gegenüber solchen Ausreißern, weil er auf Mittelwert und Streuung basiert.
Beispiel:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
# Seed für Reproduzierbarkeit
np.random.seed(42)
# Simuliere 1000 normalverteilte Werte mit Mittelwert 100, Standardabweichung 15
X = np.random.normal(loc=100, scale=15, size=(1000, 1))
# Wende MinMaxScaler an
scaler = MinMaxScaler(feature_range=(0, 10))
X_scaled = scaler.fit_transform(X)
# Daten in 1D extrahieren
X_scaled_flat = X_scaled.flatten()
# Plot der Verteilung nach MinMax-Scaling
plt.figure(figsize=(10, 5))
plt.hist(X_scaled_flat, bins=50, color='orange', edgecolor='black', alpha=0.7, density=True)
plt.title("Histogramm der MinMax-skalierten Daten (n = 1000)")
plt.xlabel("Skalierte Werte (Bereich: [0, 1])")
plt.ylabel("Dichte")
# Grenzen einzeichnen
plt.axvline(x=0, color='red', linestyle='--', label='min (0)')
plt.axvline(x=10, color='red', linestyle='--', label='max (10)')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()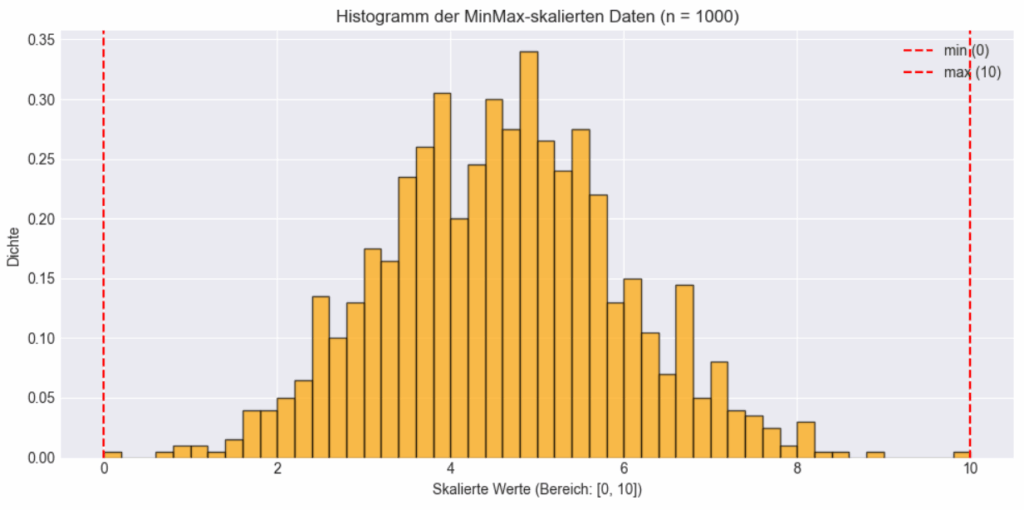
Das Histogramm zeigt die Verteilung von 1000 Datenpunkten nachdem sie mit dem MinMaxScaler transformiert wurden wobei die ursprüngliche Form der Verteilung erhalten bleibt. In dem Beispiel wurde der MinMaxScaler mit einer feature_range von 0 bis 10 initialisiert, Gibt man hier keinen Wert an, nimmt der MinMaxScaler die Werte 0 und 1 an, was in den meisten Fällen auch am besten ist.
