TODO für Tag 16
- KMeans
- Elbow-Methode zur Bestimmung der optimalen Clusteranzahl
KMeans
Der KMeans-Algorithmus für eine Aufteilung in 3 Gruppen funktioniert in etwa so: Zuerst wählt er 3 zufällige Stellen aus, die als erste Schätzungen für die Mittelpunkte einer Gruppen dienen. Dann schaut er sich jeden einzelnen Punkt an und packt ihn in die Gruppe, deren Mittelpunkt ihm am nächsten ist. Wenn alle Punkte einer Gruppe zugeordnet sind, berechnet der Algorithmus für jede Gruppe neu, wo genau die Mitte aller Punkte in dieser Gruppe liegt. Diese neuen Mitten sind dann die verbesserten Schätzungen für die Gruppenmittelpunkte. Diesen Vorgang wiederholt der Algorithmus immer wieder. Das macht er so lange, bis sich die Mittelpunkte der Gruppen kaum noch bewegen. Am Ende hat man dann die Punkte so in 3 Gruppen aufgeteilt, dass die Punkte innerhalb jeder Gruppe möglichst nah an ihrem gefundenen Mittelpunkt sind, und das sind dann die Cluster.
Die KMeans-Klasse in scikit-learn ist eine Implementierung des KMeans-Algorithmus mit wichtigen Features. Hier ein einfaches Beispiel für kMeans in scikit-learn.
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# Beispieldaten generieren
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# KMeans-Modell instanziieren
# 4 Cluster, also n_clusters=4.
# n_init='auto' (oder 10 oder mehr) für Robustheit
kmeans = KMeans(n_clusters=4, n_init='auto', random_state=42)
# Das Modell trainieren (clustern) und Clusterzuordnungen erhalten
cluster_labels = kmeans.fit_predict(X)
# Ergebnisse ausgeben
print("Zentroiden:\n", kmeans.cluster_centers_)
print("\nClusterzuordnungen für die ersten 10 Punkte:", cluster_labels[:10])
print("\nInertia (Summe der quadrierten Abstände):", kmeans.inertia_)
# Ergebnisse visualisieren
plt.scatter(X[:, 0], X[:, 1], c=cluster_labels, s=20, cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=100, c='red', marker='X', label='Zentroiden')
plt.title("KMeans Clustering")
plt.xlabel("Merkmal 1")
plt.ylabel("Merkmal 2")
plt.legend()
plt.show()Das Beispiel demonstriert das KMeans-Clustering: Zuerst wird einen Beispieldatensatz von 300 Punkten mit Hilfe der Funktion make_blobs erzeugt, der speziell darauf ausgelegt ist, 4 voneinander getrennte Gruppen zu bilden. Anschließend wird ein KMeans-Objekt aus scikit-learn initialisiert, wobei festgelegt wird, dass genau 4 Cluster gesucht werden sollen (n_clusters=4) und durch n_init=’auto‘ eine robuste Initialisierung durch mehrere unabhängige Läufe sichergestellt wird. Der Code wendet dann den KMeans-Algorithmus auf die Daten an, indem er die Methode fit_predict verwendet, mit der die optimalen 4 Cluster-Zentren gefunden und jeden Datenpunkt einem dieser Cluster zuordnet wird. Die Zuordnungen wird in der Variable cluster_labels gespeichert.
Zum Schluss gibt der Code die Koordinaten der gefundenen Cluster-Zentren aus, die Cluster-Zuordnungen für die ersten paar Datenpunkte und den ‚Inertia‘-Wert, der die Güte des Clusterings angibt, aus, bevor ein Streudiagramm erstellt wird, das die ursprünglichen Datenpunkte visuell darstellt, eingefärbt entsprechend ihrem zugewiesenen Cluster, wobei die berechneten Cluster-Zentren durch rote ‚X‘ markiert sind.
Ausgabe:
Zentroiden:
[[ 1.98258281 0.86771314]
[ 0.94973532 4.41906906]
[-1.37324398 7.75368871]
[-1.58438467 2.83081263]]
Clusterzuordnungen für die ersten 10 Punkte: [0 2 1 2 0 0 3 1 2 2]
Inertia (Summe der quadrierten Abstände): 212.00599621083478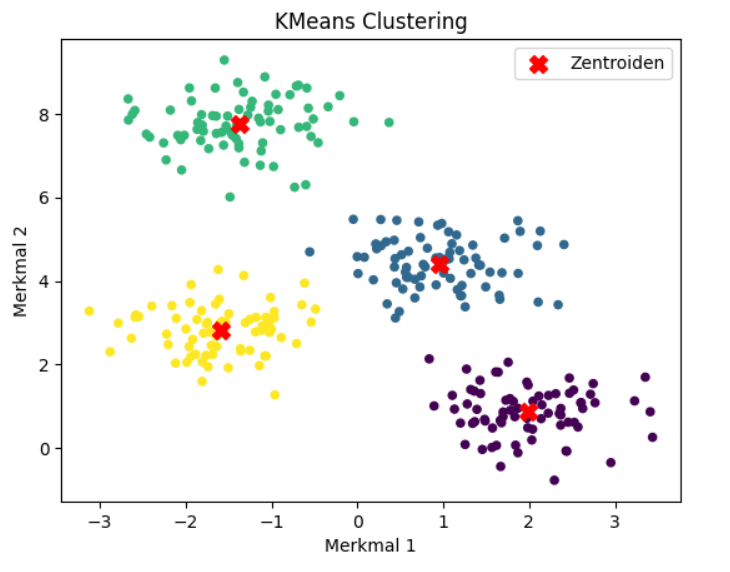
Zentroiden: Dieser Teil zeigt die Koordinaten der vier endgültigen Cluster-Zentren an, die der KMeans-Algorithmus nach dem Durchlauf gefunden hat. Da die Eingabedaten zwei Dimensionen haben, hat jede der vier Zentroiden auch zwei Koordinaten. Dies sind die rechnerischen „Mittelpunkte“ der gefundenen Cluster.
Clusterzuordnungen für die ersten 10 Punkte: Diese Liste von Zahlen zeigt, welchem der vier Cluster jeder der ersten zehn Punkte im ursprünglichen Datensatz zugeordnet wird. Die Zahlen 0, 1, 2 und 3 repräsentieren die vier verschiedenen Cluster, die gefunden wurden.
Inertia (Summe der quadrierten Abstände) repräsentiert die Summe der quadrierten euklidischen Abstände jedes Datenpunkts zu dem Zentroiden seines zugewiesenen Clusters. Dieser Wert ist das, was der KMeans-Algorithmus versucht zu minimieren; ein niedrigerer Wert bedeutet, dass die Punkte innerhalb ihrer jeweiligen Cluster näher an den Zentroiden liegen, also dass die Cluster „dichter“ sind.
Die Elbow-Methode zur Bestimmung der optimalen Clusteranzahl
Die Elbow-Methode ist eine heuristische Technik, die verwendet wird, um eine sinnvolle Anzahl von Clustern (k) für den KMeans-Algorithmus zu schätzen, wenn man diese Anzahl nicht von vornherein weiß. Sie basiert auf der Idee, wie stark die „Inertia“ abnimmt, wenn man die Anzahl der Cluster erhöht. Je mehr Cluster man verwendet, desto geringer wird die Inertia immer sein. Die Elbow-Methode sucht nach dem Punkt, an dem die Verringerung der Inertia durch Hinzufügen eines weiteren Clusters stark abnimmt. Stellt man die Inertia gegen die Anzahl der Cluster grafisch dar, sieht die Kurve oft aus wie ein gebogener Arm, und der „Ellenbogen“ (der Punkt, an dem die Krümmung am stärksten ist und die Linie flacher wird) wird als Indikator für die optimale Anzahl von Clustern interpretiert, da zusätzliche Cluster jenseits dieses Punktes nur noch marginale Verbesserungen der Inertia bringen.
Hier ein einfaches Beispiel:
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import numpy as np
# Beispieldaten generieren
# 12 Cluster, um zu sehen, ob die Elbow-Methode funktioniert
X, y = make_blobs(n_samples=1000, centers=12, cluster_std=0.60, random_state=42)
# Bereich der zu testenden Clusteranzahlen (k) definieren
k_bereich = range(1, 15)
# Inertia-Werte für jeden k speichern
inertia_werte = []
for k in k_bereich:
# KMeans-Modell für das aktuelle k instanziieren
# n_init='auto' ist wichtig, um sicherzustellen, dass mehrere Initialisierungen
# getestet werden und wir ein gutes Ergebnis für jedes k bekommen.
kmeans = KMeans(n_clusters=k, n_init='auto', random_state=42)
# Modell trainieren
kmeans.fit(X)
# Inertia (Summe der quadrierten Abstände) nach dem Training speichern
inertia_werte.append(kmeans.inertia_)
# Elbow-Diagramm plotten
plt.figure(figsize=(8, 6))
plt.plot(k_bereich, inertia_werte, marker='o') # k auf x-Achse, Inertia auf y-Achse
plt.title('Elbow-Methode zur Bestimmung der optimalen Clusteranzahl (k)')
plt.xlabel('Anzahl der Cluster (k)')
plt.ylabel('Inertia')
plt.xticks(k_bereich) # Sorgt dafür, dass alle k-Werte auf der x-Achse angezeigt werden
plt.grid(True)
plt.show()
# Man sucht visuell den Punkt im Diagramm, wo die Kurve einen deutlichen "Knick" macht
# und der Abfall danach weniger steil wird. Dies ist der "Ellenbogen".
# In diesem speziellen Beispiel mit make_blobs(centers=4) sollte der Knick
# ziemlich deutlich bei k=4 liegen.
print(f"Getestete k-Werte: {list(k_bereich)}")
print(f"Inertia-Werte für diese k: {inertia_werte}")Ausgabe:
Getestete k-Werte: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]
Inertia-Werte für diese k: [63529.69578933764, 33162.52709693149, 17437.197375870575, 9528.801769397258, 6225.045829744744, 5234.5911516926635, 2775.813983214429, 2583.276066341614, 1631.7338980144873, 1126.1155498363682, 714.709069602912, 695.0336235205137, 665.9561937399092, 609.3595060432816]
Plot:
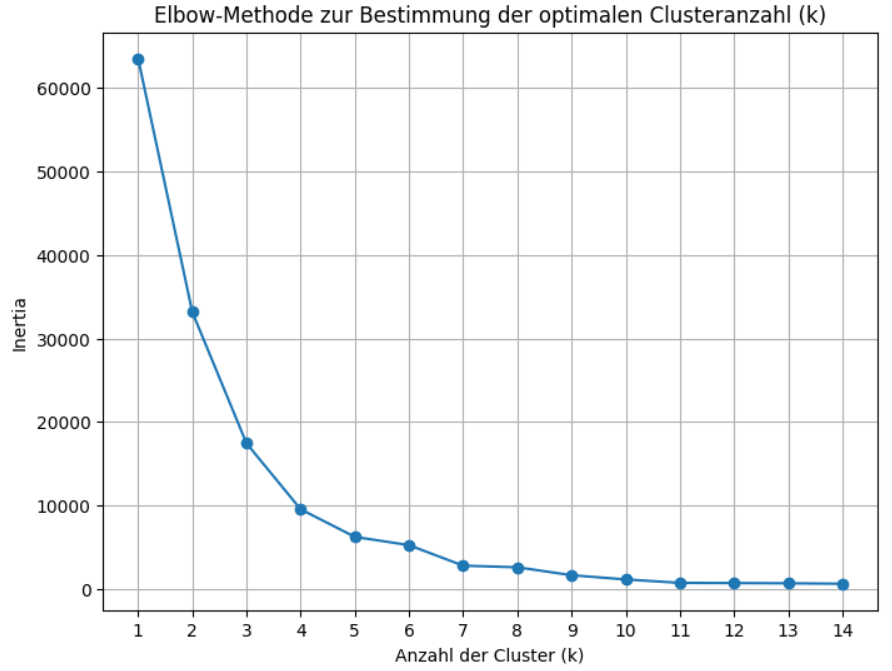
Der Plot stellt auf der horizontalen Achse die getestete Anzahl von Clustern (k) dar und auf der vertikalen Achse die sogenannte Inertia, welche die Güte des Clusterings für die jeweilige Clusteranzahl misst – ein niedrigerer Wert bedeutet, dass die Datenpunkte näher an den Zentren ihrer zugewiesenen Cluster liegen.
Die Listen bestätigen die getesteten k-Werte und liefern die exakten Inertia-Werte, die als Punkte in das Diagramm geplottet wurden. Die Kurve im Diagramm fällt zunächst sehr steil ab, was bedeutet, dass das Hinzufügen von Clustern die Inertia stark reduziert, doch um den Punkt k=4 wird der Abfall der Kurve deutlich flacher, was optisch einen „Knick“ oder „Ellenbogen“ bildet und darauf hindeutet, dass zusätzliche Cluster über vier hinaus nur noch einen vergleichsweise geringen Mehrwert in Bezug auf die Reduktion der Inertia bringen. Daher legen das Diagramm und die Werte nahe, dass vier Cluster eine sinnvolle Anzahl für diesen Datensatz sind.
Mit folgendem Code kann man die Daten/Cluster plotten.
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y, s=20, cmap='viridis')
plt.title('Cluster (generiert mit make_blobs)')
plt.xlabel('Merkmal 1')
plt.ylabel('Merkmal 2')
plt.grid(True)
plt.show()Ausgabe:
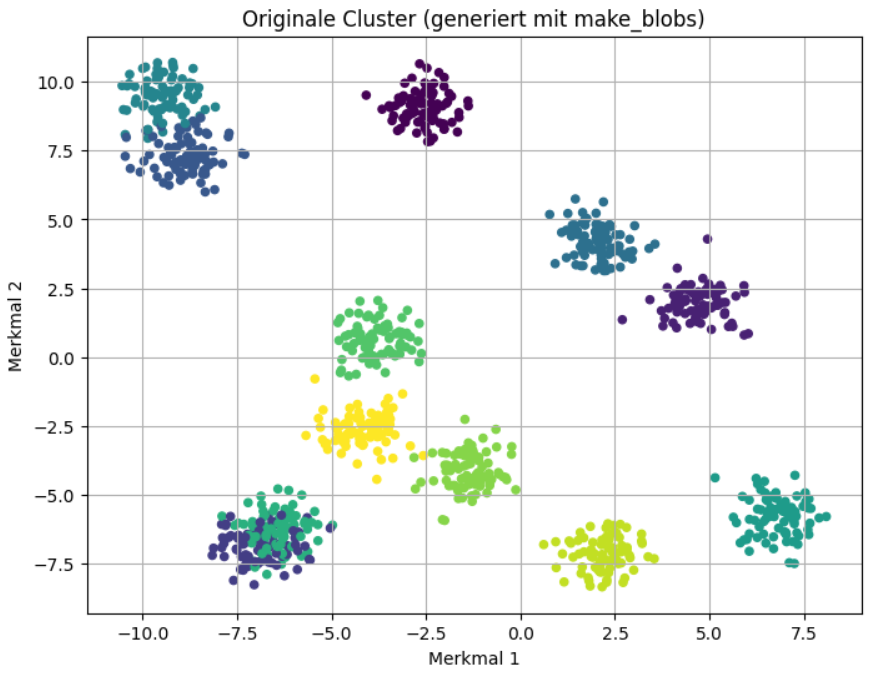
Die KMeans-Klasse in scikit-learn ist für die Elbow-Methode zur Bestimmung der optimalen Clusteranzahl gut geeignet, da sie nach dem Training direkt das Attribut inertia_ bereitstellt, das genau den Wert enthält, der für die Erstellung des Elbow-Diagramms benötigt wird. Man muss lediglich eine Schleife über die gewünschten k-Werte implementieren, um die erforderlichen Inertia-Werte zu sammeln.
