30 Tage scikit-learn – Tag 2: Erstes Modell erstellen – Klassifikation mit Iris-Datensatz

TODO für Tag 2

Dataset laden und verstehen
Daten in Trainings- und Testset aufteilen
Ein einfaches Klassifikationsmodell trainieren
Vorhersagen machen und Modell bewerten

Dataset laden (Iris-Datensatz)

Erst mal die Daten laden. Das habe ich ja gestern schon mal gemacht.

from sklearn import datasets

iris = datasets.load_iris()
X = iris.data      # Feature-Matrix: 150 Zeilen, 4 Spalten (Merkmale)
y = iris.target    # Ziel (Klassen): 0, 1 oder 2 (drei Iris-Arten)

Daten in Trainings- und Testdaten aufteilen

Beim maschinellen Lernen ist es wichtig, die verfügbaren Daten in Trainings- und Testdaten aufzuteilen. Die Trainingsdaten werden genutzt, um das Modell zu trainieren – also um Muster zu erkennen und Parameter zu lernen. Die Testdaten dienen anschließend zur Bewertung des Modells, um zu prüfen, wie gut es auf neue, unbekannte Daten generalisiert. Ein typisches Aufteilungsverhältnis ist 80 % Training und 20 % Test, kann aber je nach Anwendungsfall variieren.

from sklearn.model_selection import train_test_split

# 80% Training, 20% Test, Zufallszustand für Reproduzierbarkeit
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

print(f"Trainingsmenge: {X_train.shape[0]} Datenpunkte")
print(f"Testmenge: {X_test.shape[0]} Datenpunkte")

Einfaches Klassifikationsmodell trainieren

Dieser Python-Code zeigt, wie man ein logistisches Regressionsmodell mit scikit-learn erstellt und trainiert. Es wird das LogisticRegression-Modell aus scikit-learn importiert – ein klassisches Modell zur binären Klassifikation (z. B. „ja“ vs. „nein“).
Es wird ein Modellobjekt erstellt. Mit max_iter=200 wird festgelegt, dass das Training maximal 200 Iterationen dauern darf. Das ist wichtig, falls die Standardanzahl (meist 100) nicht zum Konvergieren reicht.
Das Modell wird mit Trainingsdaten X_train (Merkmale) und y_train (Zielwerte/Klassen) trainiert. Dabei passt es die Modellparameter so an, dass es die beste Trennlinie zwischen den Klassen findet.

from sklearn.linear_model import LogisticRegression

# Modell instanziieren
model = LogisticRegression(max_iter=200)  # max_iter: max. Anzahl Iterationen fürs Training

# Modell mit Trainingsdaten fitten
model.fit(X_train, y_train)

Vorhersagen machen und Modellbewertung

Mit model.predict kann man für einen oder mehrere Datensätze eine Vorhersage machen. Mit accuracy_scoreaus dem Modul sklearn.metrics kann man die Genauigkeit des Modells ermitteln.

Bonus: Explainable AI (XAI)

Der folgende Code verwendet SHAP (SHapley Additive exPlanations) zur Erklärung der Vorhersagen eines Machine-Learning-Modells – ein zentrales Konzept in Explainable AI (XAI). Das ist eigentlich kein sklearn Feature, aber trotzdem ganz interessant. Der shap.Explainer analysiert, wie stark jedes Feature die Vorhersage beeinflusst – basierend auf der SHAP-Theorie (aus der Spieltheorie). Die SHAP-Werte sagen aus, wie viel jedes Feature zur Abweichung vom Durchschnitt beiträgt. Das Waterfall-Plot zeigt die SHAP-Werte für eine einzelne Vorhersage – also z. B. warum das Modell bei dieser Blume gerade diesen Wert vorhergesagt hat.

Dazu muss als erstes folgendes installiert werden.

!pip install shap xgboost

Mit dem folgenden Code kann dann ermittelt werden, welches der 4 Features den größten Einfluss auf das die Vorhersage hat.

import shap

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

from sklearn.metrics import accuracy_score

iris = load_iris()
X, y = iris.data, iris.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

model = xgboost.XGBRegressor()
model.fit(X_train, y_train)

y_pred = model.predict(X_test)

explainer = shap.Explainer(model, X_train)

# SHAP-Werte berechnen
# Für Klassifizierung kann der Output für jede Klasse berechnet werden
# Die Struktur von shap_values wird shap.Explanation sein, die dies handhabt
shap_values = explainer(X_test)

# SHAP-Werte visualisieren für eine einzelne Vorhersage (z.B. die erste Instanz im Testset)
shap.plots.waterfall(shap_values[0]) # Erkläre die erste Testinstanz

Mit dem Aufruf von shap.plots.waterfall wird dann die folgenden SHAP-Wasserfall-Plot erzeugt.

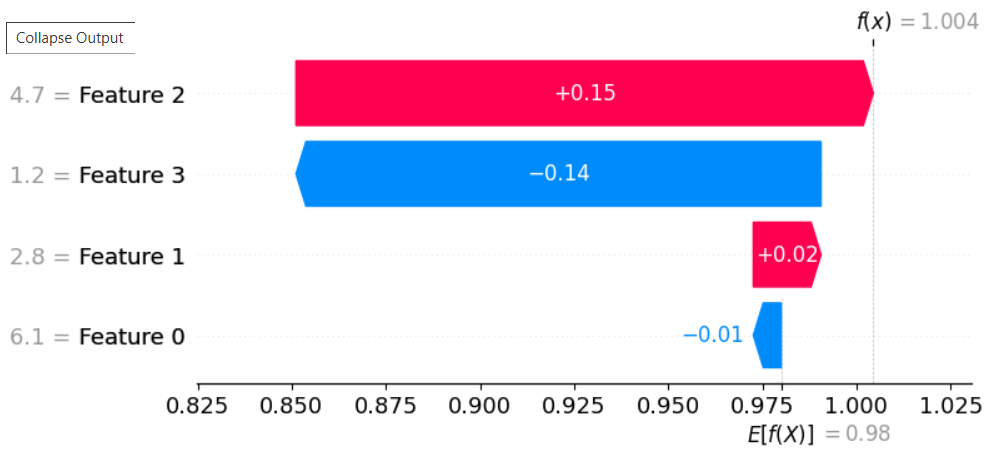
Hier sind die Kerninformationen, die der Plot vermittelt:

Basiswert (E[f(X)] = 0.98)
Dies ist der durchschnittliche vorhergesagte Wert des Modells über das gesamte Trainingsdatenset, bevor die Merkmalswerte der spezifischen Instanz berücksichtigt werden.
Vorhergesagter Wert (f(x) = 1.004)
Dies ist der tatsächliche vorhergesagte Wert des Modells für die spezifische Instanz.
Merkmale und ihr Einfluss
Die Liste auf der linken Seite zeigt die wichtigsten Features und ihre Werte. Die farbigen Balken zeigen den Einfluss jedes Features auf die Vorhersage
- Rote Balken
  Features, die dazu beitragen, den vorhergesagten Wert zu erhöhen.
- Blaue Balken
  Features, die dazu beitragen, den vorhergesagten Wert zu verringern.
- Die Länge des Balkens gibt die Größe des SHAP-Werts und damit die Stärke des Features an.
- Die Merkmale sind von oben nach unten nach der Größe ihres absoluten Einflusses (SHAP-Wert) sortiert. Das Merkmal mit dem größten positiven oder negativen Einfluss steht ganz oben.
- Feature 2 (Wert 4.7)
  Hat den größten positiven Einfluss (+0.15), verschiebt die Vorhersage am stärksten nach oben.
- Feature 3 (Wert 1.2)
  Hat den größten negativen Einfluss (-0.14), verschiebt die Vorhersage am stärksten nach unten.
- Feature 1 (Wert 2.8)
  Hat einen kleinen positiven Einfluss (+0.02).
- Feature 0 (Wert 6.1)
  Hat einen sehr kleinen negativen Einfluss (-0.01).
Der Weg von Basiswert zum Vorhergesagten Wert
Der Plot zeigt, wie der Basiswert (0.98) schrittweise durch die Beiträge der einzelnen Merkmale zum finalen vorhergesagten Wert (1.004) transformiert wird. Man startet beim Basiswert und addiert/subtrahiert die SHAP-Werte der einzelnen Merkmale nacheinander.

Der SHAP-Wasserfall-Plot erklärt, warum das Modell für diese spezifische Instanz den Wert 1.004 vorhersagt, ausgehend von einem Durchschnittswert von 0.98. Es zeigt, dass insbesondere die hohen Werte von Feature 2 und der niedrige Wert von Feature 3 den größten Einfluss auf diese Vorhersage hatten. Feature 2 erhöhte die Vorhersage deutlich, während Feature 3 sie ebenfalls deutlich verringerte, wobei der positive Einfluss von Feature 2 etwas stärker war. Die anderen gezeigten Merkmale hatten nur geringen Einfluss.

Das bedeutet aber nicht, dass man einfach die Features 0 und 1 entfernen kann und damit noch immer sehr gute Vorhersagen erzielt. Ändert man beispielsweise den random_state auf 40 was dazu führt, dass x_test und x_train anders aufgeteilt werden, sieht der Plot wiederum ganz anders aus.

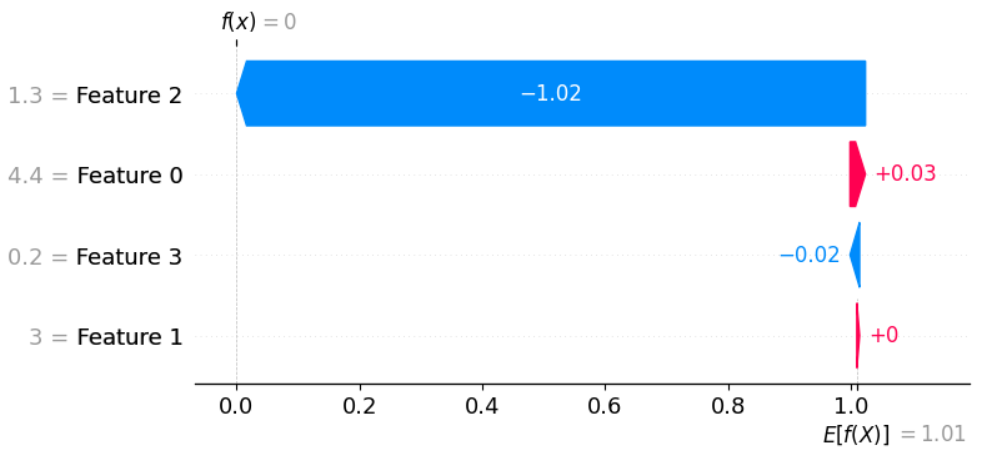
Wie man sieht ist für diese Instanz nur noch Feature 2 relevant während die Features 0,1 und 3 so gut wie keinen Einfluss auf die Vorhersage haben. Das liegt an der geänderten Aufteilung der Traings- und Testdaten.