TODO für Tag 28
- Komplexere Pipelines mit Preprocessing-Schritten
Komplexere Pipelines mit Preprocessing-Schritten
Das Preprocessing in scikit-learn habe ich in den vorherigen Übungen (Tag 13, Tag 15, Tag 19, Tag 21, etc.) schon ausreichend behandelt und das Prinzip sollte klar sein. Aber die Datenvorbereitung kann vielfältige Formen annehmen. Neben den üblichen Verdächtigen wie Imputationsstrategien zum Umgang mit fehlenden Daten, dem TfidfVectorizer zum Extrahieren gewichteter Textmerkmale oder der Skalierung Numerische Features um sicherzustellen, dass Modelle nicht durch unterschiedliche Wertebereiche beeinflusst werden, gibt es noch viele andere Preprocessing-Schritte die man anwenden kann. Für kategorische Daten ist z.B. eine Umwandlung in ein numerisches Format notwendig (One-Hot-Encoding). Hierfür wird für jede Kategorie eine neue binäre Spalte erstellt.
Ein Thema, dass ich aber im Zusammenhang mit dem Preprocessing in einer Pipeline noch nicht bearbeitet habe ist das Erstellen einer eigenen Preprocessing Funktion und da es keinen direkten Preprocessing-Schritt gibt, der eine zyklische Variable wie die Uhrzeit (0-24 Uhr) so darstellt, sodass der Übergang von 23:59 Uhr zu 00:00 Uhr als kontinuierlich wahrgenommen wird, wird in heute der „CyclicalHourEncoder“ eine Sinus/Kosinus-Transformation erstellt. Dies lässt sich mit dem FunctionTransformer in scikit-learn realisieren.
Implementierung des CyclicalHourEncoder mit FunctionTransformer:
import numpy as np
import pandas as pd
from sklearn.preprocessing import FunctionTransformer
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
import matplotlib.pyplot as plt # Importiere matplotlib
# Beispieldaten mit einer 'Uhrzeit'-Spalte (0-23)
data = pd.DataFrame({'Uhrzeit': np.arange(0, 25), 'Anderes_Merkmal': np.random.rand(25)*2-1})
# Funktion für die Transformation
def sin_cos_transformer_01(X):
"""
Transformiert eine Spalte (angenommen als erste Spalte von X)
mit Stunden (0-23.99) in zwei Spalten:
- Sinus-Komponente
- Kosinus-Komponente
"""
# Stellt sicher, dass X ein 2D-Array ist, falls es als Series kommt
X_np = np.array(X)
if X_np.ndim == 1:
X_np = X_np.reshape(-1, 1)
winkel = (X_np[:, 0] / 24.0) * 2 * np.pi # Nimmt die erste (und einzige) Spalte
sin_zeit = (np.sin(winkel))
cos_zeit = (np.cos(winkel))
return np.column_stack((sin_zeit, cos_zeit))
# Erstellen des FunctionTransformers
time_encoder_01 = FunctionTransformer(sin_cos_transformer_01, feature_names_out=lambda self, input_features: ['hour_sin', 'hour_cos'])
# Verwendung in einem ColumnTransformer (typischer Anwendungsfall)
preprocessor = ColumnTransformer(
transformers=[('zeit_features', time_encoder_01, ['Uhrzeit'])],
remainder='passthrough' # Andere Spalten unverändert lassen
)
# Pipeline erstellen
pipeline = Pipeline(steps=[('preprocessor', preprocessor)])
# Pipeline anwenden
transformed_data_array = pipeline.fit_transform(data) # Gibt ein NumPy Array zurück
# Namen der Features aus der Pipeline holen
feature_names = pipeline.get_feature_names_out()
transformed_df = pd.DataFrame(transformed_data_array, columns=feature_names)
print("\nNamen der Features:")
print(list(feature_names)) # Ausgabe der Feature-Namen zur Überprüfung
# Namen der Sinus- und Kosinus-Spalten im transformed_df identifizieren
# Diese Namen hängen von den Namen im ColumnTransformer und der Pipeline ab.
sin_col_name = 'zeit_features__hour_sin'
cos_col_name = 'zeit_features__hour_cos'
anderes_merkmal = 'remainder__Anderes_Merkmal'
# Wenn Sie 'Anderes_Merkmal' auch plotten wollten (obwohl es nicht transformiert wurde und eine andere Skala hat):
# other_col_name = 'preprocessor__remainder__Anderes_Merkmal'
# Erstellen des Liniendiagramms
plt.figure(figsize=(12, 7))
# Plotten der Sinus-Komponente
plt.plot(data['Uhrzeit'], transformed_df[sin_col_name], label=f'{sin_col_name.split("__")[-1]} ', marker='o', linestyle='-')
# Plotten der Kosinus-Komponente
plt.plot(data['Uhrzeit'], transformed_df[cos_col_name], label=f'{cos_col_name.split("__")[-1]} ', marker='x', linestyle='--')
# Plotten von anderes_merkmal
plt.plot(data['Uhrzeit'], transformed_df[anderes_merkmal], label=f'{anderes_merkmal.split("__")[-1]} ', marker='x', linestyle='--')
# Diagramm anpassen
plt.title('Zyklische Transformation der Uhrzeit (0-24 Uhr) mit Sinus und Kosinus')
plt.xlabel('Uhrzeit (Stunde des Tages)')
plt.ylabel('Transformierter Wert')
plt.xticks(np.arange(0, 25, 2)) # Stellt sicher, dass alle Stunden angezeigt werden oder in Schritten
plt.yticks(np.arange(-1.1, 1.1, 0.1)) # Y-Achse von -1 bis 1
plt.legend()
plt.grid(True, which='both', linestyle='--', linewidth=0.5)
plt.tight_layout()
plt.show()Ausgabe:
Namen der Features: ['zeit_features__hour_sin', 'zeit_features__hour_cos', 'remainder__Anderes_Merkmal']
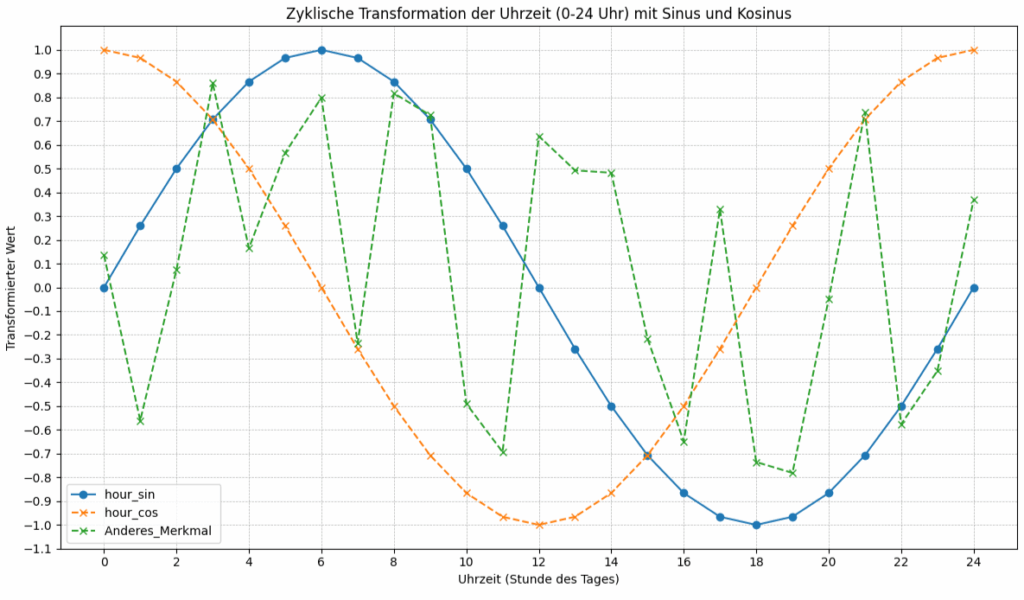
Das Bild zeigt ein Liniendiagramm der zyklischen Transformation der Uhrzeit (0-24 Uhr) mit Sinus und Kosinus“. Auf der x-Achse ist die „Uhrzeit (Stunde des Tages)“ von 0 bis 24 aufgetragen. Auf der y-Achse ist der „Transformierte Wert“ dargestellt, der von -1.0 bis 1.0 reicht.
Im Diagramm sind drei Linien dargestellt:
Die Blaue Linie repräsentiert die Sinus-Transformation der Uhrzeit. Sie erreicht ihr Maximum von 1.0 bei Stunde 6. Sie durchläuft den Nullpunkt bei Stunde 12. Sie erreicht ihr Minimum von -1.0 bei Stunde 18 und kehrt bei Stunde 24 zum Wert 0 zurück. Dies ist das typische Verhalten einer Sinusfunktion über einen vollständigen Zyklus (2π).
Die Orangefarbene Linie repräsentiert die Kosinus-Transformation der Uhrzeit. Sie startet bei Stunde 0 mit einem Wert von 1.0. Sie durchläuft den Nullpunkt bei Stunde 6. Sie erreicht ihr Minimum von -1.0 bei Stunde 12. Sie durchläuft den Nullpunkt erneut bei Stunde 18 und kehrt bei Stunde 24 zum Wert 1.0 zurück. Dies ist das typische Verhalten einer Kosinusfunktion über einen vollständigen Zyklus.
Grüne Linie zeigt einen zackigen Verlauf. Diese zufälligen Werte sind mit „np.random.rand(25)*2-1}“ erstellt worden und repräsentieren ein zusätzliches Feature. Es wurde nicht zyklisch transformiert, sondern durch remainder=’passthrough‘ unverändert weitergegeben.
Die Sinus- und Kosinus-Transformationen in diesem Diagramm erzeugen Werte im Bereich von -1 bis +1. Die hier dargestellten Kurven entsprechen den Standard-Sinus- und Kosinuswerten, die durch die Umrechnung der Stunde in einen Winkel (0 bis 2π) und die Anwendung der trigonometrischen Funktionen entstehen.
Die zyklische Transformation der Uhrzeit bietet den Vorzug, die tatsächliche Natur der Zeit, nämlich ihren wiederkehrenden Charakter, für ein maschinelles Lernmodell verständlich zu machen. Ohne eine solche Umwandlung würde ein Modell beispielsweise die Stunde 23 als weit entfernt von der Stunde 0 interpretieren, obwohl in der Realität nur ein kurzer Moment zwischen 23:59 Uhr und 00:00 Uhr liegt. Durch die Abbildung der Zeit auf einen Kreis mittels Sinus- und Kosinus wird diese künstliche Distanz eliminiert.
Der CyclicalHourEncoder kann z.B. als Alternative für den OneHotEncoder verwendet werden, wenn man z.B. in der Pipeline die Stunden einer Uhrzeit mit dem OneHotEncoder in 24 neue, meist spärlich besetzte Features umwandelt, was bei Modellen, die empfindlich auf hohe Dimensionalität reagieren, problematisch sein kann und die Gefahr von Overfitting erhöht. Die zyklische Methode hingegen kommt mit lediglich zwei dichten Merkmalen aus, was den Merkmalsraum kompakter hält und oft zu einer besseren Generalisierungsfähigkeit des Modells führt.
Während der OneHotEncoder die diskrete, kategoriale Natur jeder einzelnen Stunde betont und keine Beziehungen zwischen ihnen herstellt, fokussiert sich die zyklische Transformation mit dem CyclicalHourEncoder auf die kontinuierliche und periodische Eigenschaft der Zeit. Für die meisten Anwendungen, die Zeitreihen oder periodische Verhaltensweisen modellieren, bietet die zyklische Darstellung eine überlegene Methode, um dem Modell die zugrundeliegende Struktur der Zeit effektiv zu vermitteln und seine Lernfähigkeit für zeitabhängige Muster zu verbessern. Der OneHotEncoder bricht diese Struktur auf und behandelt jede Stunde isoliert.
Das folgende Beispiel vergleicht die zyklische Transformation mit dem OneHotEncoder indem es einen künstlichen Datensatz erstellt, der einen zeitlichen Verlauf über mehrere Tage simuliert. Für jeden Tag werden 24 Datenpunkte generiert. Das Hauptmerkmal ist die Stunde des Tages, die sich zyklisch wiederholt. Ein Zielwert wird so konstruiert, dass er eine sinusförmige Abhängigkeit von dieser Stunde aufweist, zusätzlich versehen mit einem zufälligen Rauschen, um eine realitätsnahe, periodische Zeitreihe darzustellen, deren Werte beispielsweise tagsüber höher und nachts niedriger sind.
Nach der Datenerstellung wird der Datensatz in Trainings- und Testmengen aufgeteilt, wobei die ‚hour‚-Spalte als Eingabemerkmal und die ‚target‚-Spalte als Zielvariable dient.
Der Kern des Beispiels liegt in der Definition und dem Vergleich zweier unterschiedlicher Vorverarbeitungs- und Modellierungspipelines für das Stundenmerkmal. Die erste Pipeline implementiert die zyklische Transformation. Die zweite Pipeline verwendet stattdessen einen OneHotEncoder für die ‚hour‘-Spalte. Dieser Ansatz erzeugt für jede der 24 Stunden ein separates binäres Merkmal. Auch hier werden die resultierenden Merkmale nach dem One-Hot-Encoding standardmäßig skaliert, bevor sie demselben Typ von Ridge-Regressionsmodell übergeben werden.
Im Anschluss werden beide Pipelines jeweils auf den Trainingsdaten trainiert. Mit den trainierten Modellen werden dann Vorhersagen für die Testdaten generiert. Die Güte dieser Vorhersagen wird anhand MSE und R2 Scores bewertet.
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import FunctionTransformer, OneHotEncoder, StandardScaler
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.linear_model import Ridge # Ein lineares Modell ist gut für den Vergleich
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
# Erstellen Daten für mehrere Tage, um genügend Samples zu haben.
np.random.seed(42)
n_days = 20
samples_per_day = 24
total_samples = n_days * samples_per_day
# Stunden (0-23 wiederholend)
hours = np.tile(np.arange(samples_per_day), n_days)
# Erzeuge ein zyklisches Signal für den Zielwert
# z.B. eine Sinuswelle, die von der Stunde abhängt, mit etwas Rauschen
# Der Winkel geht von 0 bis 2*pi für 0-23 Stunden
angle = (hours / float(samples_per_day)) * 2 * np.pi
# Zielwert: z.B. höhere Werte am Tag, niedrigere in der Nacht
target = 5 * np.sin(angle - np.pi/2) + 10 # Verschiebung, damit Peak tagsüber ist
target += np.random.normal(0, 1.5, total_samples) # Rauschen hinzufügen
data = pd.DataFrame({'hour': hours, 'target': target})
print("Beispieldaten:")
print(data.head())
print(f"\nForm der Daten: {data.shape}")
# Aufteilen in Trainings- und Testdaten
X = data[['hour']]
y = data['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Preprocessing-Pipelines definieren
# a) Zyklische Transformation
def cyclical_transformer_neg1_pos1(X_in):
"""Transformiert Stunden (0-23) in Sinus/Kosinus-Werte (-1 bis 1)."""
X_np = np.array(X_in)
if X_np.ndim == 1:
X_np = X_np.reshape(-1, 1)
# Stelle sicher, dass die Stunde für die Winkelberechnung im Bereich 0-23 liegt
hour_of_day = X_np[:, 0] % 24
angle_rad = (hour_of_day / 24.0) * 2 * np.pi
sin_time = np.sin(angle_rad)
cos_time = np.cos(angle_rad)
return np.column_stack((sin_time, cos_time))
cyclical_features = FunctionTransformer(
cyclical_transformer_neg1_pos1,
feature_names_out=lambda self, input_features: ['hour_sin', 'hour_cos']
)
# Preprocessor für zyklische Features
# StandardScaler ist hier optional, kann aber oft helfen.
cyclical_preprocessor = ColumnTransformer(
transformers=[
('cyclical', cyclical_features, ['hour'])
],
remainder='passthrough'
)
pipeline_cyclical = Pipeline(steps=[
('preprocessor', cyclical_preprocessor),
('scaler', StandardScaler()), # Skalieren nach der Transformation
('regressor', Ridge(alpha=1.0))
])
# b) OneHotEncoder Transformation
# StandardScaler ist hier auch optional, aber konsistent.
ohe_preprocessor = ColumnTransformer(
transformers=[
('onehot', OneHotEncoder(handle_unknown='ignore', sparse_output=False), ['hour'])
],
remainder='passthrough'
)
pipeline_ohe = Pipeline(steps=[
('preprocessor', ohe_preprocessor),
('scaler', StandardScaler()), # Skalieren nach der Transformation
('regressor', Ridge(alpha=1.0))
])
# Modelle trainieren und evaluieren
# Modell mit zyklischer Transformation
pipeline_cyclical.fit(X_train, y_train)
y_pred_cyclical = pipeline_cyclical.predict(X_test)
mse_cyclical = mean_squared_error(y_test, y_pred_cyclical)
r2_cyclical = r2_score(y_test, y_pred_cyclical)
print("\n--- Modell mit zyklischer Transformation ---")
print(f"Mean Squared Error: {mse_cyclical:.4f}")
print(f"R2 Score: {r2_cyclical:.4f}")
# Modell mit OneHotEncoder
pipeline_ohe.fit(X_train, y_train)
y_pred_ohe = pipeline_ohe.predict(X_test)
mse_ohe = mean_squared_error(y_test, y_pred_ohe)
r2_ohe = r2_score(y_test, y_pred_ohe)
print("\n--- Modell mit OneHotEncoder ---")
print(f"Mean Squared Error: {mse_ohe:.4f}")
print(f"R2 Score: {r2_ohe:.4f}")
# Ergebnisse plotten
# Um die Ergebnisse sinnvoll zu plotten werden die Testdaten nach der Stunde sortiert
# Es wird nur einen Ausschnitt der Testdaten (z.B. die ersten ~48 Stunden) verwendet
plot_df = X_test.copy()
plot_df['hour_of_day'] = plot_df['hour']
plot_df['y_true'] = y_test
plot_df['y_pred_cyclical'] = y_pred_cyclical
plot_df['y_pred_ohe'] = y_pred_ohe
# Sortieren für einen sauberen Linienplot über einige Tage
# Plotten der Vorhersagen für die Stunden 0-23 für einige Wiederholungen
# Um einen typischen Tagesverlauf zu sehen, werden die Durchschnittsvorhersage pro Stunde verwendet
avg_predictions_cyclical = plot_df.groupby('hour_of_day')['y_pred_cyclical'].mean()
avg_predictions_ohe = plot_df.groupby('hour_of_day')['y_pred_ohe'].mean()
avg_true = plot_df.groupby('hour_of_day')['y_true'].mean()
hours_for_plot = avg_predictions_cyclical.index
plt.figure(figsize=(14, 8))
# Plot der durchschnittlichen wahren Werte
plt.plot(hours_for_plot, avg_true, label='Durchschnittliche wahre Werte', color='black', linestyle=':', linewidth=2, marker='o')
# Plot der Vorhersagen des zyklischen Modells
plt.plot(hours_for_plot, avg_predictions_cyclical, label=f'Zyklisch (MSE: {mse_cyclical:.2f}, R2: {r2_cyclical:.2f})', color='blue', linestyle='-', linewidth=2, marker='^')
# Plot der Vorhersagen des OHE-Modells
plt.plot(hours_for_plot, avg_predictions_ohe, label=f'OneHotEncoder (MSE: {mse_ohe:.2f}, R2: {r2_ohe:.2f})', color='red', linestyle='--', linewidth=2, marker='x')
plt.title('Vergleich: Zyklische vs. OneHotEncoder Transformation für Uhrzeit')
plt.xlabel('Stunde des Tages')
plt.ylabel('Zielwert (Vorhersage/Wahr)')
plt.xticks(np.arange(0, 24, 1))
plt.legend()
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()Ausgabe:
Beispieldaten: hour target 0 0 5.745071 1 1 4.962974 2 2 6.641406 3 3 8.749011 4 4 7.148770 Form der Daten: (480, 2) --- Modell mit zyklischer Transformation --- Mean Squared Error: 2.1755 R2 Score: 0.8472 --- Modell mit OneHotEncoder --- Mean Squared Error: 2.2918 R2 Score: 0.8390
Die Ergebnisse deuten auf eine leichte Überlegenheit der Pipeline hin, die die zyklische Transformation für das Stundenmerkmal verwendet, verglichen mit der Pipeline, die auf den OneHotEncoder setzt.
Das Modell mit der zyklischen Transformation erreicht einen MSE von 2.1755, während das Modell mit dem OneHotEncoder einen MSE von 2.2918 erzielt. R2 Score zeigt ein ähnliches Bild. Das zyklische Modell erreicht 0.8472, was bedeutet, dass etwa 84,72% der Varianz in den Zieldaten durch dieses Modell erklärt werden können. Das OneHotEncoder-Modell hingegen kommt auf einen R2 Score von 0.8390, also erklärt es etwa 83,90% der Varianz.
Zusammenfassend lässt sich sagen, dass die Pipeline mit der zyklischen Transformation der Uhrzeit in diesem spezifischen Szenario zu einem präziseren Modell führt. Die Fähigkeit dieser Transformation, die kontinuierliche und periodische Natur der Stunde besser zu repräsentieren, ermöglicht es dem Modell, die zugrundeliegenden Muster in den Daten effektiver zu lernen.
Das folgende Diagramm visualisiert den Vergleich der beiden Modelle noch einmal.
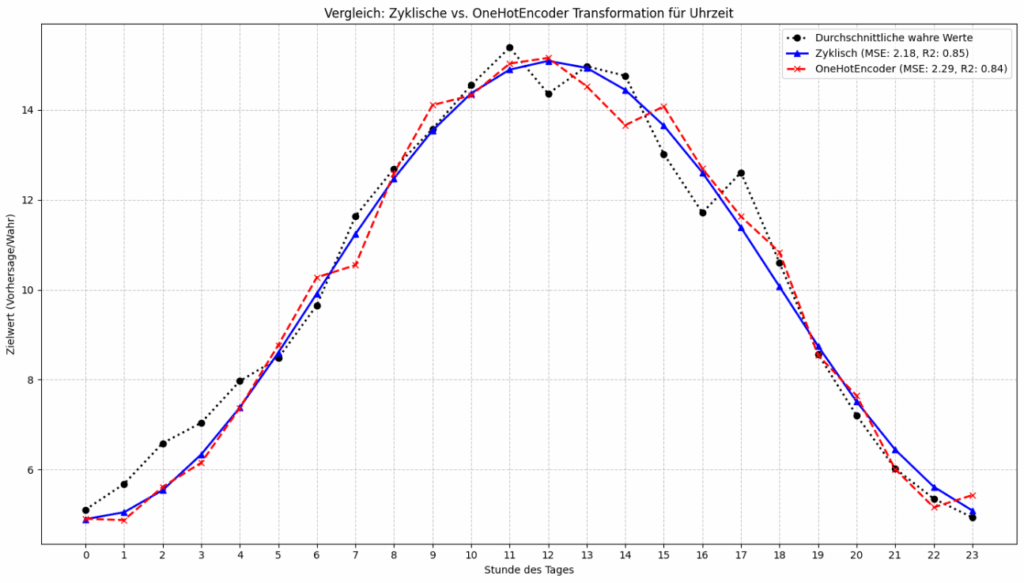
Die schwarze Linie stellt die durchschnittlichen wahren Zielwerte für jede Stunde des Tages dar. Sie zeigt ein glattes, sinusähnliches Muster mit einem Tiefpunkt in den frühen Morgenstunden, einem Anstieg zu einem Maximum um die Mittagszeit und einem anschließenden Abfall zu den späten Abendstunden. Dies ist das Muster, das die Modelle lernen sollen.
Die blaue Linie repräsentiert die durchschnittlichen Vorhersagen des Modells, das die zyklische Transformation der Uhrzeit verwendet hat. Diese Linie schmiegt sich sehr eng an die schwarze Linie der wahren Werte an. Sie bildet den glatten, wellenförmigen Verlauf sehr gut nach und zeigt nur geringe Abweichungen.
Die rote Linie zeigt die durchschnittlichen Vorhersagen des Modells, das den OneHotEncoder für die Stunden verwendet hat. Obwohl auch diese Linie dem generellen Trend der wahren Werte folgt, ist sie sichtbar „eckiger“ und weniger glatt als die blaue Linie. Sie weist an einigen Stellen deutlichere Abweichungen von der schwarzen Linie auf und scheint die feineren Nuancen der Kurve nicht ganz so präzise zu erfassen.
