Tag 30 ist erreicht! Die vergangenen Wochen waren eine spannende Reise durch die Welt des maschinellen Lernens mit scikit-learn. Die heutige Aufgabe ist es, möglichst viel von dem gelernten in einem eigenen Projekt zu bündeln.
Für das Projekt greife ich auf einen alten Datensatz zurück. Dabei handelt es sich um die IMU-Daten (Inertial Measurement Unit) eines Projektes das leider nicht erfolgreich beendet wurde. Gemeinsam mit zwei Freunden haben wir versucht, mittels des 6-Achsen-Sensors von Google Wear-OS Watches verschiedene Fitnessübungen (Liegestützen, Bizeps Curls, etc.) in Echtzeit auf dem Handy zu erkennen, Wiederholungen zu zählen und Nutzern Tipps zur Erreichung der Trainingsziele zu geben. Auch wenn das Projekt leider nicht den erhofften Erfolg hatte, leben die Daten und die Idee weiter. Für das Projekt habe ich seinerzeit Tensorflow verwendet und als Modell war ein Recurrent and Residual U-Net wie hier beschrieben Einsatz das sehr gute Ergebnisse erzielt hat.
Die Frage die ich heute klären möchte ist: Kann ein Framework wie scikit-learn bei der Klassifizierung von Fitnessübungen und der Extraktion von Wiederholungen aus Sensordaten mit einem komplexen Deep Learning Modell mithalten?
Schritt 1: Laden der Daten und verstehen
Die Daten werden aus einem kleinen Tool heruntergeladen, dass ich seinerzeit für das Labeln der Daten verwendet habe. Mit dem kleinen Tool konnte man den IMU Sensordaten sehr schnell und einfach die Label der Übungen zuweisen.
Screenshot Label-Tool für IMU Daten
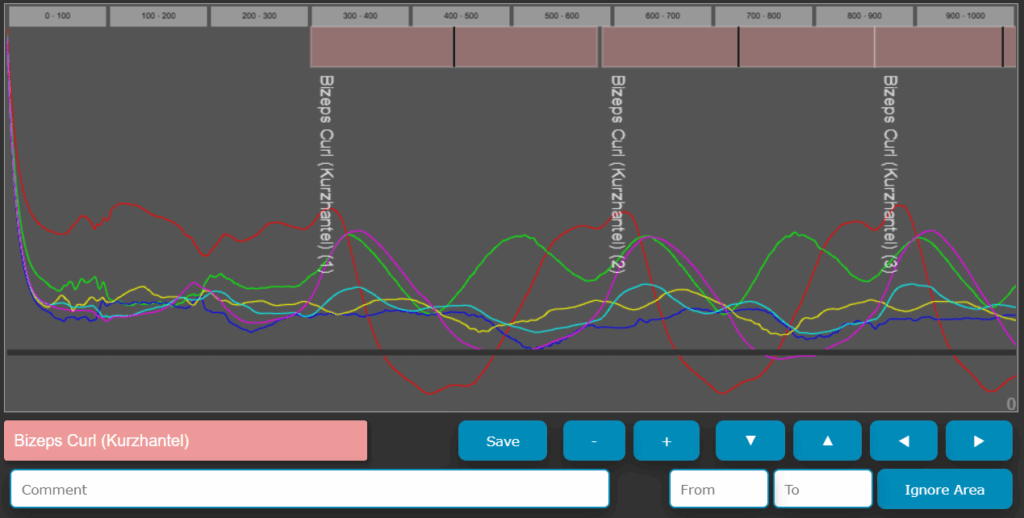
Für die Beispiel-Implementierung habe ich die Dateien hier als Zip-Datei abgelegt und zum Download zur Verfügung gestellt. In der Datei enthalten sind 25 CSV Dateien mit den gelabelten Sensordaten.
Die Labels findet man in der folgenden CSV Datei.
Das Laden der Labels und der Daten erfolgt dann mit folgendem Code. Darüber hinaus enthält das Code-Fragment alle Imports die nötig sind und die Konfiguration aller folgenden Codeblöcke.
import sys
import os
import glob
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix, ConfusionMatrixDisplay
from sklearn.model_selection import GridSearchCV, train_test_split, cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
# Data File settings
labels_file = "labels.csv"
train_files_directory = "downloads"
data_file_pattern = "data_*.csv"
label_id_column_index = 8 # 9th column is index 8 (0-indexed)
# Define windowing parameters
window_length = 192 # Number of timesteps in each window
overlap_percentage = 0.9 # 90% overlap
# Aufgmentation settings
noise_factor = 0.2
# Train Test Split settings
test_size = 0.80 # 80% for testing, 20% for training (80/20 because of window overlap and augmented data)
# Read the labels.csv file
df_labels = pd.read_csv(labels_file, encoding='utf-8')
# Ensure 'id' column is integer for merging
df_labels['id'] = df_labels['id'].astype(int)
print(f"Successfully read '{labels_file}'")
print (df_labels)
# Find, read, and combine all data files
full_pattern = os.path.join(train_files_directory, data_file_pattern)
data_file_paths = glob.glob(full_pattern)
if not data_file_paths:
print(f"No files found matching pattern '{full_pattern}' in directory '{train_files_directory}'.")
print(f"Found the following train files: {data_file_paths}")
all_dfs = [] # List to hold individual DataFrames
for file_path in data_file_paths:
try:
df_temp = pd.read_csv(file_path, delimiter=';', header=None)
if not df_temp.empty:
all_dfs.append(df_temp)
print(f"Successfully read and added: {file_path} ({len(df_temp)} rows)")
else:
print(f"Warning: The file '{file_path}' is empty and was skipped.")
except pd.errors.EmptyDataError:
print(f"Warning: The file '{file_path}' is empty and was skipped.")
except Exception as e:
print(f"Error reading '{file_path}': {e}. This file will be skipped.")
if not all_dfs:
print("No valid train data could be read from any files. Exiting.")
# Concatenate all DataFrames in the list into one
df = pd.concat(all_dfs, ignore_index=True)
print(f"\nCombined train DataFrame has {len(df)} rows from {len(all_dfs)} file(s).")
df.shapeAusgabe:
Successfully read 'labels.csv'
id name
0 0 Kein Workout
1 1 Ab Wheel
2 2 Arnold Press
3 3 Around the World
4 4 Hyperextension
.. ... ...
196 196 Aufrechtes Rudern (Kabel)
197 197 Aufrechtes Rudern (Kurzhantel)
198 198 V Up
199 199 Gehen (Laufband)
200 200 Zercher Squat (Langhantel)
[201 rows x 2 columns]
Found the following train files: ['downloads\\data_10.csv', 'downloads\\data_11.csv', 'downloads\\data_12.csv', 'downloads\\data_13.csv', 'downloads\\data_14.csv', 'downloads\\data_15.csv', 'downloads\\data_16.csv', 'downloads\\data_17.csv', 'downloads\\data_18.csv', 'downloads\\data_19.csv', 'downloads\\data_2.csv', 'downloads\\data_20.csv', 'downloads\\data_21.csv', 'downloads\\data_22.csv', 'downloads\\data_23.csv', 'downloads\\data_24.csv', 'downloads\\data_25.csv', 'downloads\\data_26.csv', 'downloads\\data_3.csv', 'downloads\\data_4.csv', 'downloads\\data_5.csv', 'downloads\\data_6.csv', 'downloads\\data_7.csv', 'downloads\\data_8.csv', 'downloads\\data_9.csv']
Successfully read and added: downloads\data_10.csv (5604 rows)
Successfully read and added: downloads\data_11.csv (2015 rows)
Successfully read and added: downloads\data_12.csv (2540 rows)
Successfully read and added: downloads\data_13.csv (3381 rows)
Successfully read and added: downloads\data_14.csv (2231 rows)
Successfully read and added: downloads\data_15.csv (2167 rows)
Successfully read and added: downloads\data_16.csv (2160 rows)
Successfully read and added: downloads\data_17.csv (2073 rows)
Successfully read and added: downloads\data_18.csv (2171 rows)
Successfully read and added: downloads\data_19.csv (2194 rows)
Successfully read and added: downloads\data_2.csv (1667 rows)
Successfully read and added: downloads\data_20.csv (2086 rows)
Successfully read and added: downloads\data_21.csv (2623 rows)
Successfully read and added: downloads\data_22.csv (2270 rows)
Successfully read and added: downloads\data_23.csv (2287 rows)
Successfully read and added: downloads\data_24.csv (2589 rows)
Successfully read and added: downloads\data_25.csv (1429 rows)
Successfully read and added: downloads\data_26.csv (995 rows)
Successfully read and added: downloads\data_3.csv (2534 rows)
Successfully read and added: downloads\data_4.csv (1640 rows)
Successfully read and added: downloads\data_5.csv (2224 rows)
Successfully read and added: downloads\data_6.csv (2298 rows)
Successfully read and added: downloads\data_7.csv (2493 rows)
Successfully read and added: downloads\data_8.csv (2912 rows)
Successfully read and added: downloads\data_9.csv (3546 rows)
Combined DataFrame has 60129 rows from 25 file(s).
(60129, 10)
Nun sind alle Daten in einen Pandas Dataframe geladen. Als erstes ist es wichtig, zu prüfen, on es sich um einen „balancierten“ Datensatz handelt, weil es die Qualität des trainierten Modells maßgeblich beeinflusst. Das folgende Code-Fragment gibt die Anzahl der vorhandenen Zeilen pro Label aus.
try:
# Ensure the column index is valid for the combined DataFrame
if label_id_column_index < len(df.columns):
label_ids = df.iloc[:, label_id_column_index].astype(int)
else:
print(f"Error: Column index {label_id_column_index} is out of bounds for the combined train data ({len(df.columns)} columns found).")
print("Please check if all train files have at least that many columns and the correct delimiter.")
except KeyError: # Might happen if iloc fails due to unexpected column structure
print(f"Error: Could not access column at index {label_id_column_index}. Check train file structure.")
except Exception as e:
print(f"An unexpected error occurred while processing label IDs: {e}")
label_counts = label_ids.value_counts().reset_index()
label_counts.columns = ['id', 'count'] # Rename columns for clarity and merging
# Merge counts with label names
merged_data = pd.merge(label_counts, df_labels[['id', 'name']], on='id', how='left')
merged_data['name'] = merged_data['name'].fillna('Unknown Label (ID: ' + merged_data['id'].astype(str) + ')')
merged_data = merged_data.sort_values(by='count', ascending=False)
print (merged_data)So sieht die Ausgabe aus. Man sieht deutlich, dass die Label 43 und 31 stark unterrepräsentiert sind. Eine einfache Lösung ist es, das Modell nur auf die Label 127 (Liegestütz) und 19 (Bizeps Curl Kurzhantel) zu trainieren.
id count name
0 0 26206 Kein Workout
1 19 16684 Bizeps Curl (Kurzhantel)
2 127 14356 Liegestütz
3 43 2098 Crunch
4 31 785 Dip
Der folgende Code visualisiert die Daten noch mal in einem Diagramm:
if not merged_data.empty:
plt.figure(figsize=(12, 8)) # Adjust figure size as needed
bars = plt.bar(merged_data['name'], merged_data['count'], color='skyblue')
plt.xlabel("Exercise Name")
plt.ylabel("Number of Rows")
plt.title(f"Number of Rows per Exercise Label (from {len(all_dfs)} train file(s))")
plt.xticks(rotation=45, ha="right", fontsize=10)
plt.yticks(fontsize=10)
plt.tight_layout()
for bar in bars:
yval = bar.get_height()
plt.text(bar.get_x() + bar.get_width()/2.0, yval + 0.01 * merged_data['count'].max(), int(yval), ha='center', va='bottom', fontsize=9)
plt.show()
else:
print("No data to plot. Check if train files contain valid label IDs present in labels.csv.")
print("\n--- Label Counts (Combined from all files) ---")
print(merged_data[['name', 'count', 'id']])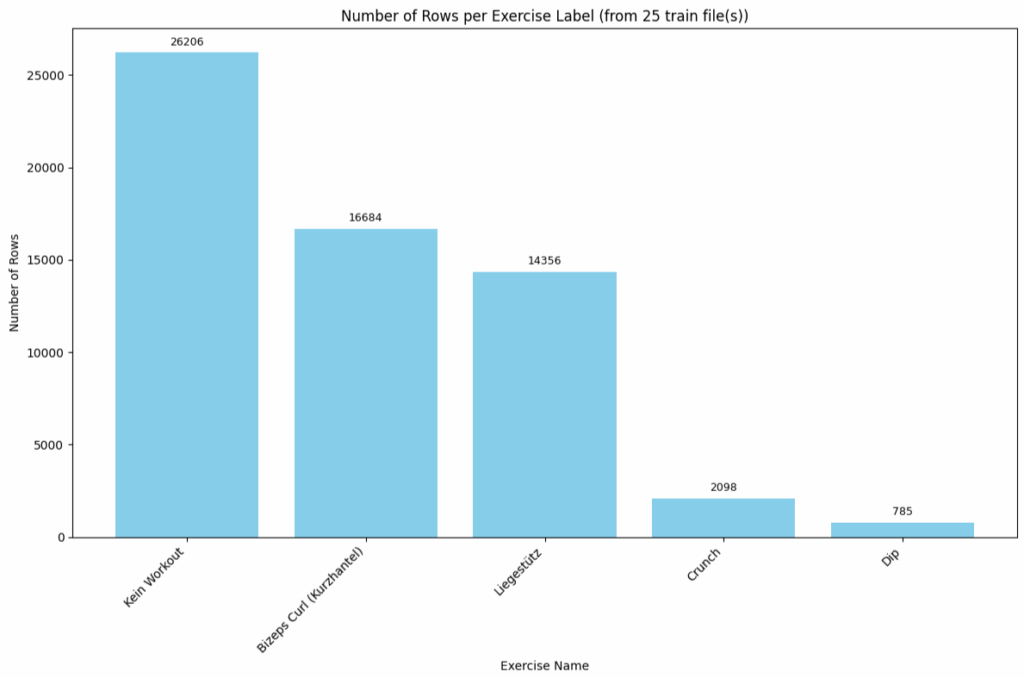
--- Label Counts (Combined from all files) ---
name count id
0 Kein Workout 26206 0
1 Bizeps Curl (Kurzhantel) 16684 19
2 Liegestütz 14356 127
3 Crunch 2098 43
4 Dip 785 31
Das Balkendiagramm zeigt die Verteilung der Datenpunkte (Anzahl der Zeilen) der verschiedenen Übungen. Jeder Balken repräsentiert eine Übung und seine Höhe entspricht der Anzahl der Datenzeilen für diese Kategorie.
Man erkennt eine deutliche Unausgewogenheit in den Datenmengen: „Kein Workout“ hat mit Abstand die meisten Datenpunkte, gefolgt von „Bizeps Curl (Kurzhantel)“ und „Liegestütz“. Die Übungen „Crunch“ und „Dip“ sind im Vergleich dazu stark unterrepräsentiert.
- Kein Workout: ca. 26206 Zeilen (der höchste Balken)
- Bizeps Curl (Kurzhantel): ca. 16684 Zeilen
- Liegestütz: ca. 14356 Zeilen
- Crunch: ca. 2098 Zeilen
- Dip: ca. 785 Zeilen (der niedrigste Balken)
Der Dataframe hat 10 Spalten von denen die Spalten 1-6 die IMU Sensordaten enthalten und die Spalten 8 und 9 ein zusammengesetztes Label (dazu später mehr) darstellen. Alle anderen Spalten können entfallen, da hier keine relevanten Informationen für das Training enthalten sind.
0 1 2 3 4 5 6 7 8 9
0 0 29005 35904 39034 32782 32744 32710 10 0 0
1 9 28971 35910 39117 32833 32754 32698 10 0 0
2 19 28958 35883 39173 32887 32763 32693 10 0 0
3 38 29006 36023 39282 32940 32746 32685 10 0 0
4 48 28993 36226 39436 32984 32734 32687 10 0 0
... ... ... ... ... ... ... ... ... ... ...
60124 33758 25594 30813 33774 32611 31753 32481 10 0 0
60125 33767 25656 30755 33736 32604 31714 32492 10 0 0
60126 33777 25642 30635 33778 32595 31739 32506 10 0 0
60127 33786 25592 30623 33626 32622 31782 32483 10 0 0
60128 33796 25558 30709 33468 32693 31874 32522 10 0 0
60129 rows × 10 columns
Mit df.drop kann man die überflüssigen Spalten entfernen.
df = df.drop(0, axis=1)
df = df.drop(7, axis=1)Der Dataframe enthält nun nur noch 8 Spalten. Die Spaltenbezeichnungen 1-6 und 8+9 bleiben erhalten, wenn man mit df.drop die Spalten entfernt.
1 2 3 4 5 6 8 9
0 29005 35904 39034 32782 32744 32710 0 0
1 28971 35910 39117 32833 32754 32698 0 0
2 28958 35883 39173 32887 32763 32693 0 0
3 29006 36023 39282 32940 32746 32685 0 0
4 28993 36226 39436 32984 32734 32687 0 0
... ... ... ... ... ... ... ... ...
60124 25594 30813 33774 32611 31753 32481 0 0
60125 25656 30755 33736 32604 31714 32492 0 0
60126 25642 30635 33778 32595 31739 32506 0 0
60127 25592 30623 33626 32622 31782 32483 0 0
60128 25558 30709 33468 32693 31874 32522 0 0
60129 rows × 8 columnsDas Label setzt sich aus den 2 Komponenten der Spalte 8 und 9 zusammen. Wobei in Spalte 8 die Übung steht (0, 127,19, etc.) und in Spalte 9 steht, ob es sich um den ersten Teil einer Wiederholung handelt oder den zweiten Teil. Jede Übung im Gym hat eine bestimmte Bewegungsfolge, die ich in 2 Teile geteilt habe um besser die Wiederholungen zählen zu können.
Beispiel: Liegestütz
| Spalte 8 | Spalte 9 | Übung |
| 127 | 1 | Liegestütz Abwärts-Teil |
| 127 | 2 | Liegestütz Aufwärts-Teil |
Das Trennen von Features und Label erfolgt dann mit der Funktion df.iloc.
df_x = df.iloc[:, 0:6]
df_y = df.iloc[:, 6:8]Der Dataframe df_x enthält nun nur noch die Sensordaten und nicht mehr das Label.
1 2 3 4 5 6
0 29005 35904 39034 32782 32744 32710
1 28971 35910 39117 32833 32754 32698
2 28958 35883 39173 32887 32763 32693
3 29006 36023 39282 32940 32746 32685
4 28993 36226 39436 32984 32734 32687
... ... ... ... ... ... ...
60124 25594 30813 33774 32611 31753 32481
60125 25656 30755 33736 32604 31714 32492
60126 25642 30635 33778 32595 31739 32506
60127 25592 30623 33626 32622 31782 32483
60128 25558 30709 33468 32693 31874 32522
60129 rows × 6 columns
In der Variable df_y stehen die Lable-Daten.
8 9
0 0 0
1 0 0
2 0 0
3 0 0
4 0 0
... ... ...
60124 0 0
60125 0 0
60126 0 0
60127 0 0
60128 0 0
60129 rows × 2 columns
die beiden Teile des Labels müssen vor dem Training noch in eine einzelne Zeile umgewandelt werden, da ein Classifier in er Regel nur ein Label vorhersagt. Dazu werden die Spalten wie folgt kombiniert.
df_y2 = df_y[8].astype(str) + '_' + df_y[9].astype(str)
df_y2Damit wird der erste Teil des Labels und der zweite Teil des Labels zu einem String zusammengefasst und als Trennzeichen ein „_“ eingefügt.
0 0_0
1 0_0
2 0_0
3 0_0
4 0_0
...
60124 0_0
60125 0_0
60126 0_0
60127 0_0
60128 0_0
Length: 60129, dtype: object
Um zu prüfen, ob alle Label vorhanden sind kann man mit unique alle eindeutigen Werte identifizieren.
unique_labels = df_y2.unique()
unique_labelsarray(['0_0', '43_1', '43_2', '127_1', '127_2', '19_1', '19_2', '31_1',
'31_2'], dtype=object)
Schritt 2: Sliding Windows erstellen und Daten bereinigen
Die Daten können in ihrer aktuellen Form nicht zum Training eines Modells genutzt werden, da die 6 „Features“ einer Zeile nicht eindeutig sind, um die gerade ausgeführte Übung zu identifizieren. Eine einfache Lösung für dieses Problem sind Sliding Windows. Sie dienen bei der Klassifikation von Zeitreihendaten dazu, das Problem zu bewältigen, dass Klassifikationsalgorithmen in der Regel eine Eingabe mit fester Länge erwarten, während Zeitreihen oft variabel lang sind und ihre dynamische Natur berücksichtigt werden muss. Sliding Windows sind Fenster fester Länge sequenziell über die gesamte Zeitreihe geschoben. Für jede Position dieses Fensters wird der darin enthaltene Ausschnitt der Zeitreihen-Daten als ein einzelner Feature-Vektor mit einem zugeordneten Label für den Klassifikator betrachtet. Durch das Verschieben des Fensters mit einer festen Schrittweite (die auch Überlappungen zulässt) wird die ursprüngliche Zeitreihe in einen Datensatz transformiert, der aus vielen einzelnen gleich langen Segmenten besteht. Die zugehörigen Labels werden aus den Labeln des Sliding Windows ermittelt. Z.B. indem man das Label aus der Mitte des Sliding Windows nimmt.
Die folgende Funktion erzeugt die Feature-Vektoren der Sliding Windows aus den Zeitreihen-Daten. Um das Label jedes Feature-Vektors zu bestimmen nimmt die Funktion das Label, dass sich in der zeitlichen Mitte dieses Fensters befindet und legt es als Label für den resultierenden Feature-Vektor fest.
def create_sliding_windows(data, window_size, step_size, y_data=None):
"""
Creates sliding windows from multivariate time series data.
Args:
data (np.ndarray or pd.DataFrame): The input multivariate time series data.
Shape should be (n_timesteps, n_features).
window_size (int): The number of timesteps in each window.
step_size (int): The number of timesteps to slide forward for the next window.
Overlap = window_size - step_size.
y_data (np.ndarray or pd.Series, optional): Corresponding labels for each timestep.
If provided, labels for each window will also be generated.
The label for a window is typically taken from the last timestep in that window,
or the most frequent label if labels can change within a window.
Here, we'll take the label of the last timestep. Shape (n_timesteps,).
Returns:
np.ndarray: A 3D array of windows, shape (n_windows, window_size, n_features).
np.ndarray (optional): If y_data is provided, a 1D array of labels for each window,
shape (n_windows,).
"""
if isinstance(data, pd.DataFrame):
X_values = data.values
elif isinstance(data, np.ndarray):
X_values = data
else:
raise ValueError("Data must be a NumPy array or Pandas DataFrame")
if y_data is not None:
if isinstance(y_data, pd.Series):
y_values = y_data.values
elif isinstance(y_data, np.ndarray):
y_values = y_data
else:
raise ValueError("y_data must be a NumPy array or Pandas Series")
if len(X_values) != len(y_values):
raise ValueError("X_data and y_data must have the same number of timesteps.")
n_timesteps = X_values.shape[0]
n_features = X_values.shape[1]
if window_size > n_timesteps:
print(f"Warning: window_size ({window_size}) is larger than total timesteps ({n_timesteps}). Returning empty arrays.")
if y_data is not None:
return np.empty((0, window_size, n_features)), np.empty((0,))
else:
return np.empty((0, window_size, n_features))
windows = []
labels = []
start_index = 0
while start_index + window_size <= n_timesteps:
end_index = start_index + window_size
window = X_values[start_index:end_index, :]
windows.append(window)
if y_data is not None:
# Common strategy: label of the middle point
middle_point = int(start_index + (window_size/2))
window_label = y_values[middle_point]
labels.append(window_label)
start_index += step_size
if y_data is not None:
return np.array(windows), np.array(labels)
else:
return np.array(windows)Die Parameter window_length = 192 und overlap_percentage = 0.9 legen fest, dass jeder Feature Vektor 192×6 Sensor-Werte enthält und das einen Overlap von 90% für die Sliding Window Verarbeitung zwischen aufeinanderfolgenden Fenstern bedeutet.
# Calculate step_size from overlap
hop_length = int(window_length * (1 - overlap_percentage))
# Ensure step is at least 1
if hop_length < 1:
print ("Warning: Hop length is < 1. Set to 1")
hop_length = 1
print(f"\nWindow Length: {window_length}")
print(f"Step Size (Hop Length): {hop_length}")
print(f"Overlap samples: {window_length - hop_length}")
windows_X_df, windows_y_df = create_sliding_windows(df_x, window_length, hop_length, y_data=df_y2)Ausgabe:
Window Length: 192
Step Size (Hop Length): 19
Overlap samples: 173
Zum Prüfen der Daten kann man sich ja mal einen Ausschnitt mit matplotlib anzeigen lassen.
# Print a part of the windows_y_df array
test_frame = windows_y_df[1850:2350]
x_positions = np.arange(len(test_frame))
plt.figure(figsize=(40, 12))
plt.bar(x_positions, test_frame, color='skyblue')
plt.xlabel("Categories / Index")
plt.ylabel("Values / Heights")
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.tight_layout()
plt.show()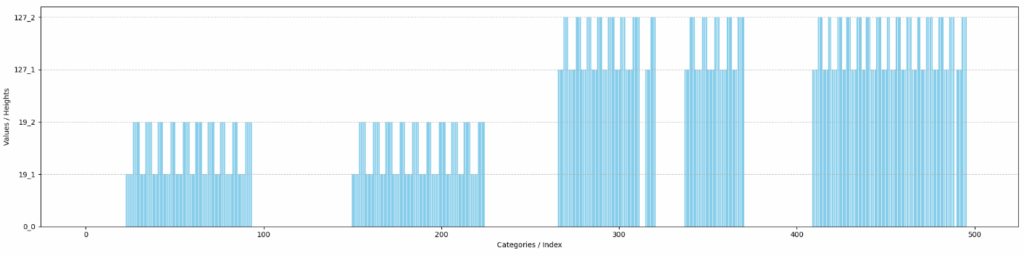
Man sieht deutlich, dass die Übungen jeweils einen Aufwärts- und eine Abwärts-Anteil besitzen, die abwechselnd aufeinanderfolgen. Bei einem zu großen Wert in window_length würde dieses Muster nicht so gut zu erkennen sein. Bei einem zu kleinen Wert für window_length könnten die Features möglicherweise nicht ausreichen, um die Übung zu identifizieren. Hier ist un Zukunft noch Finetuning möglich.
Als nächstes werden die Daten bereinigt. Wie man in dem folgenden Bild sieht, sind neben den Bizeps-Curls und den Liegestützen noch andere Übungen enthalten, die aus den Daten entfernt werden da es nicht ausreichend Daten zu den Übungen gibt, um ein Modell darauf zu trainieren.
def print_label_distribution (windows_y_df):
unique_values, counts = np.unique(windows_y_df, return_counts=True)
print ("Unique Labels:", unique_values)
print ("Count: ", counts)
x_positions = np.arange(len(unique_values))
plt.figure(figsize=(10, 6)) # Optional: Adjust figure size
plt.bar(x_positions, counts, color='c', edgecolor='black', alpha=0.8) # 'c' is cyan
# 4. Add labels, title, and customize
plt.xlabel("Unique Values")
plt.ylabel("Frequency / Count")
plt.title("Frequency Distribution of Values")
plt.xticks(x_positions, unique_values)
if any(isinstance(val, str) and len(val) > 3 for val in unique_values):
plt.xticks(x_positions, unique_values, rotation=45, ha="right")
plt.grid(axis='y', linestyle='--', alpha=0.7)
for i in range(len(unique_values)):
plt.text(x=x_positions[i],
y=counts[i] + (counts.max()*0.01),
s=str(counts[i]),
ha='center')
plt.tight_layout()
plt.show()
print_label_distribution (windows_y_df)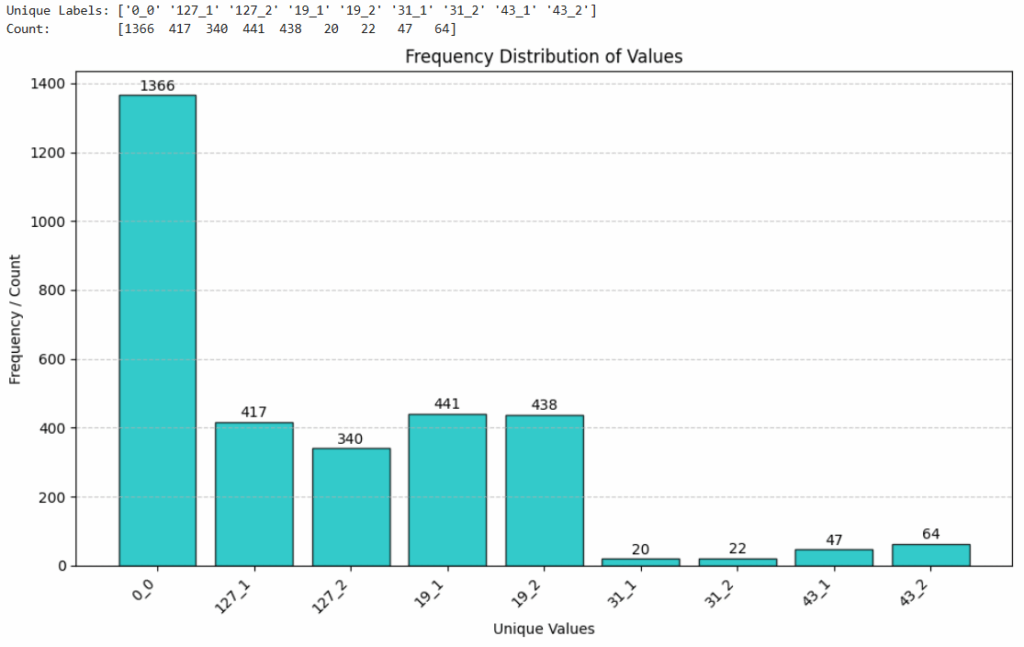
Die folgenden Zeilen entfernen alle Daten mit den Labeln ’31_1′, ’31_2′, ’43_1′ und ’43_2′. Diese werden hier für das Experiment ausgeschlossen da die ausgewählten Dateien zu wenig Daten zu den Übungen enthalten.
# Remove all data with Labels 31, 43
values_to_find_1d = ['31_1', '31_2', '43_1', '43_2']
boolean_mask_1d = np.isin(windows_y_df, values_to_find_1d)
indices_tuple_1d = np.where(boolean_mask_1d)
windows_y_df_new = np.delete(windows_y_df, indices_tuple_1d)
unique_values_new, counts = np.unique(windows_y_df_new, return_counts=True)
windows_X_df_new = np.delete(windows_X_df, indices_tuple_1d, axis=0)
print ("All data features ", windows_X_df.shape)
print ("All data labels ", windows_y_df.shape)
print ("Selected data features ", windows_X_df_new.shape)
print ("Selected data lables ", windows_y_df_new.shape)
print_label_distribution (windows_y_df_new)Damit sind alle überflüssigen Daten aus dem Datensatz entfernt und es sind nur noch die Label 0_0, 127_1, 127_2, 19_1 und 19_2 vorhanden. Das Balkendiagramm zeigt die Anzahl der Sliding Windows in dem verbleibenden Datensatz.
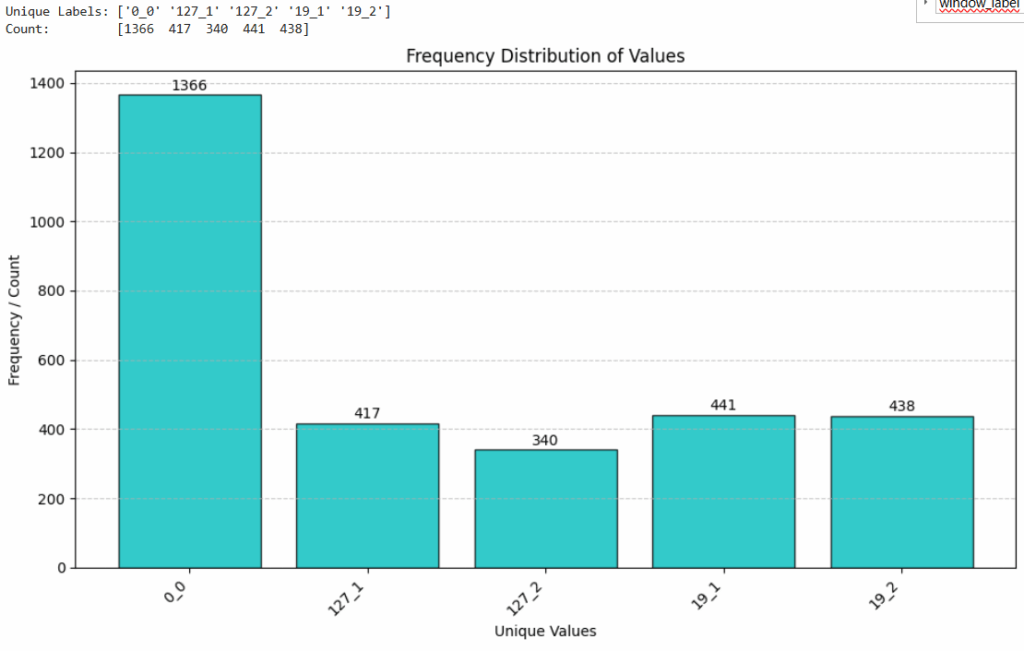
Leider haben die unterschiedlichen Label keine gleichmäßige Verteilung in den Daten. Das Label 0_0 („Kein Workout“) liegt klar vorne. Dieses Label wird von dem Label-Tool vergeben, wenn kein Label für eine Übung vergeben wurde. Also am Anfang und am Ende des Workouts und in den Satz-Pausen – von denen ich wohl viele mache :-).
Um das zu lösen, werden die Daten der Übungen 127 und 19 einfach „augmentiert„. Das bedeutet, es werden synthetische Daten erzeugt, bis die Verteilung einigermaßen gleichmäßig ist. Leider kann man diese Time-Series Daten nicht einfach mit SMOTE (Siehe Tag 26) verdoppeln, da SMOTE zufällig eine Instanz aus der Minderheitsklasse wählt und die k nächsten Nachbarn (k-nearest neighbors, KNN) identifiziert, die ebenfalls zur gleichen Klasse gehören. Einer dieser Nachbarn wird zufällig ausgewählt und ein neuer, synthetischer Datenpunkt wird entlang einer gedachten Linie erzeugt, die den ursprünglichen Feature-Vektor und den ausgewählten Nachbarn im Merkmalsraum verbindet. Die Position dieses neuen Punktes wird zufällig entlang dieser Linie gewählt. Das Problem ist, das SMOTE die zeitliche Natur der Daten innerhalb eines Fensters nicht versteht. Es interpoliert einfach zwischen den Feature-Vektoren zweier Fenster was zu stark veränderten Daten führen kann, die nicht für Training/Validation verwendet werden können.
Es gibt verschiedene andere Methoden den Datensatz ausgeglichener zu gestalten. Die einfachste Lösung ist es wohl die Daten klonen und zu verrauschen. So werden ähnliche Daten erzeugt, die nicht 100% identisch mit den vorhandenen Daten sind.
Das Erzeugen von verrauschten Kopien der existierenden Daten erfolgt mit folgendem Code-Fragment.
def add_noise_to_imu_window(imu_window, noise_type="gaussian", noise_level_factor=0.05, clip_to_original_range=False):
"""
Adds noise to a single IMU window (e.g., 196x6).
Args:
imu_window (np.ndarray): The input IMU data window, shape (timesteps, channels).
Example: (196, 6).
noise_type (str): Type of noise to add. "gaussian" or "uniform".
noise_level_factor (float): A factor to scale the noise.
For Gaussian: factor * channel_std_dev.
For Uniform: noise will be in [-factor*channel_std_dev, factor*channel_std_dev].
clip_to_original_range (bool): If True, clips the noisy data to the min/max range
of the original window's respective channels.
Returns:
np.ndarray: The IMU window with added noise.
"""
if not isinstance(imu_window, np.ndarray):
raise TypeError("imu_window must be a NumPy array.")
if imu_window.ndim != 2:
raise ValueError("imu_window must be a 2D array (timesteps, channels).")
noisy_window = imu_window.copy()
num_timesteps, num_channels = imu_window.shape
if clip_to_original_range:
min_vals_original = np.min(imu_window, axis=0)
max_vals_original = np.max(imu_window, axis=0)
# Calculate standard deviation for each channel (column)
# If a channel has std=0 (constant values), noise_scale for it will be 0.
channel_stds = np.std(imu_window, axis=0)
if noise_type == "gaussian":
# Scale for Gaussian noise based on each channel's standard deviation
noise_scales = channel_stds * noise_level_factor
# Generate noise: mean=0, scale=noise_scales (broadcasts per channel)
noise = np.random.normal(loc=0.0, scale=noise_scales, size=(num_timesteps, num_channels))
noisy_window += noise
elif noise_type == "uniform":
# Determine the limits for uniform noise based on each channel's standard deviation
# This makes the magnitude somewhat comparable to the Gaussian approach
limit_per_channel = channel_stds * noise_level_factor
# Generate noise: low=-limit, high=limit (broadcasts per channel)
# np.random.uniform expects 'low' and 'high' to be broadcastable or match the size.
# We need to generate noise column by column if limits are different per column,
# or ensure broadcasting works as expected.
# A simpler way: generate uniform noise in [-1, 1] and then scale.
noise = np.random.uniform(low=-1.0, high=1.0, size=(num_timesteps, num_channels))
noise = noise * limit_per_channel # Broadcasting limit_per_channel (num_channels,)
noisy_window += noise
else:
raise ValueError("Unsupported noise_type. Choose 'gaussian' or 'uniform'.")
if clip_to_original_range:
# Clip each channel to its original min/max
for i in range(num_channels):
noisy_window[:, i] = np.clip(noisy_window[:, i], min_vals_original[i], max_vals_original[i])
return noisy_window
augment_values_to_find_1d = ['127_1', '127_2', '19_1', '19_2']
augment_boolean_mask_1d = np.isin(windows_y_df_new, augment_values_to_find_1d)
augment_indices_tuple_1d = np.where(augment_boolean_mask_1d)
augment_indices_tuple_1d
windows_y_df_for_augmentation = windows_y_df_new[augment_indices_tuple_1d]
windows_X_df_for_augmentation = windows_X_df_new[augment_indices_tuple_1d]
print ("Featues for augmentation ", windows_y_df_for_augmentation.shape)
print ("Labels for augmentation ", windows_X_df_for_augmentation.shape)
# Convert ot float64 for augmentation
windows_X_df_for_augmentation = windows_X_df_for_augmentation.astype('float64')
windows_X_df_noise = np.zeros(windows_X_df_for_augmentation.shape)
for i in range(windows_X_df_for_augmentation.shape[0]):
windows_X_df_noise[i] = add_noise_to_imu_window(windows_X_df_for_augmentation[i],
noise_type="gaussian",
noise_level_factor=noise_factor,
clip_to_original_range=True)
windows_X_df_noise.shape
windows_X_df_sum = np.vstack((windows_X_df_new, windows_X_df_noise))
windows_y_df_sum = np.concat((windows_y_df_new, windows_y_df_for_augmentation))
print_label_distribution (windows_y_df_sum)
Ausgabe:
(array([ 184, 185, 186, ..., 2971, 2972, 2973], shape=(1636,)),)
Featues for augmentation (1636,)
Labels for augmentation (1636, 192, 6)
(1636, 192, 6)
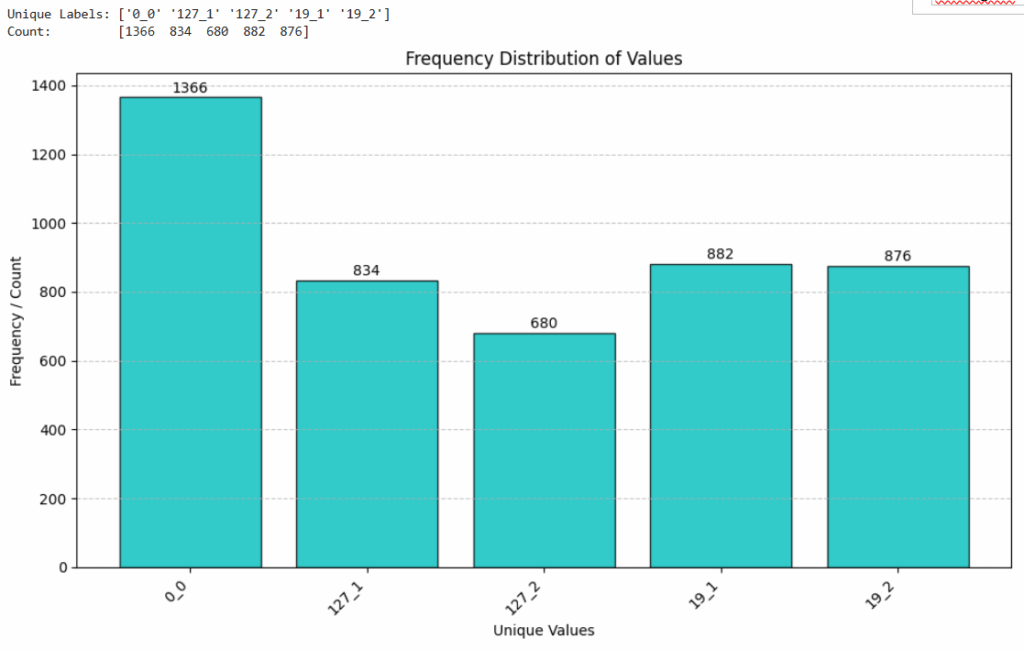
Die Anzahl der Datensätze pro Label in dem Balkendiagramm sieht schon wesentlich ausgeglichener aus. Wie man sieht ist die Anzahl der Datensätze für die Label 127 und 19 gestiegen und die Anzahl der Datensätze für das Label 0_0 ist gleich geblieben, da nur die Datensätze mit den Labeln 127 und 19 augmentiert wurden. Um noch mehr Balance in die Daten zu bekommen rufe ich die add_noise_to_imu_window Funktion noch einmal auf. Wichtig ist, dass man der Funktion die ursprünglichen Daten übergibt und nicht die verrauschten Kopien, da sonst verrauschte Daten noch weiter verrauscht werden. Sicher hätte man das auch eleganter lösen können statt die Funktion einfach so oft aufzurufen, bis die Daten einigermaßen gleichmäßig über alle Label verteilt sind, aber so ist es erst mal einfacher. Hier gibt es noch Potential …
windows_X_df_noise2 = np.zeros(windows_X_df_for_augmentation.shape)
for i in range(windows_X_df_for_augmentation.shape[0]):
windows_X_df_noise2[i] = add_noise_to_imu_window(windows_X_df_for_augmentation[i],
noise_type="uniform",
noise_level_factor=noise_factor,
clip_to_original_range=True)
windows_X_df_sum2 = np.vstack((windows_X_df_sum, windows_X_df_noise))
windows_y_df_sum2 = np.concat((windows_y_df_sum, windows_y_df_for_augmentation))
print_label_distribution (windows_y_df_sum2)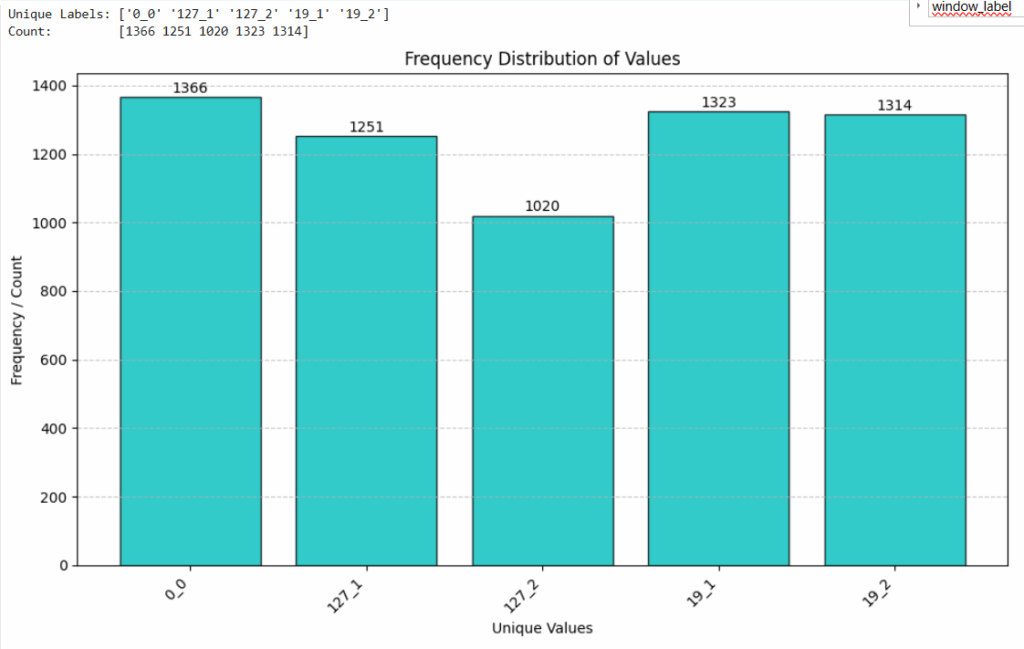
Die Daten sind jetzt schön regelmäßig über alle Label verteilt und die überflüssigen Daten der Übungen Crunch und Dip sind entfernt. Das ist zwar nicht die beste Lösung, aber für den ersten Wurf reicht es erst mal.
Schritt 3: Training eines Modells
Für das Training werde die Daten noch umformatiert, da jedes Sliding-Window momentan noch ein 2D-Array ist. Also wird die Struktur der Daten von 192×6 zu 1152×1 umgewandelt, ohne die eigentlichen Daten inhaltlich zu verändern.
windows_X_df_sum2_flat = windows_X_df_sum2.reshape(windows_X_df_sum2.shape[0], -1)All features shape (6274, 1152)
All labels shape (6274,)
Damit ist alles vorbereitet und die Daten können in Traings- und Testdaten aufgeteilt werden. Test Size ist hier mit 80% festgelegt. Das bedeutet, das nur 20% der Daten für das Training verwendet werden. In den meisten Fällen geht man genau den umgekehrten Weg und nimmt 80% der Daten für das Training und 20% für den Test. Da aber die Sliding-Windows ein Overlap von 90% haben und die Daten der Labels 127 und 19 zweimal augmentiert wurden wodurch dadurch sehr viele ähnlich Datensätze entstanden sind verwende ich nur 20% der Daten für das Training und 80% für die Validierung.
X_train, X_test, y_train, y_test = train_test_split(
windows_X_df_sum2_flat,
windows_y_df_sum2,
shuffle=True,
stratify=windows_y_df_sum2,
test_size=test_size,
random_state=42,
)
print ("Train features shape", X_train.shape)
print ("Trein labels shape ", y_train.shape)
print ("Test features shape ", X_test.shape)
print ("Test labels shape ", y_test.shape)Train features shape (1254, 1152)
Trein labels shape (1254,)
Test features shape (5020, 1152)
Test labels shape (5020,)
Der RandomForestClassifier erscheint mir als gute Wahl für dieses Problem. Wie schon unter https://www.jentsch.io/30-tage-scikit-learn-tag-9-random-forest/ beschrieben, hat der RandomForestClassifier viele Vorteile gegenüber anderen Algorithmen, wie z.B. der Umgang mit hochdimensionalen Daten und verbesserte Genauigkeit bei komplexen Datensätzen. Um die beste Anzahl an Estimators zu finden wird GridSearchCV verwendet. Nach dem Training wird die die Accuracy der unterschiedlichen Estimators (10, 20, 50, 100, 150, 200, 250, 300) in einem Plot ausgegeben und das Beste Model ausgewählt (best_model).
rf_classifier = RandomForestClassifier(
n_estimators=64, # Number of trees in the forest
random_state=42,
n_jobs=-1,
)
pipeline = Pipeline([
('scaler', StandardScaler()),
('classifier', rf_classifier)
])
param_grid = {
'classifier__n_estimators': [10, 20, 50, 100, 150, 200, 250, 300] # Values to try
}
grid_search = GridSearchCV(
estimator=pipeline,
param_grid=param_grid,
cv=5,
scoring='accuracy',
verbose=1,
n_jobs=-1,
return_train_score=True
)
print("Starting GridSearchCV...")
grid_search.fit(X_train, y_train)
print("GridSearchCV finished.")
print(f"Best parameters found: {grid_search.best_params_}")
print(f"Best cross-validation accuracy: {grid_search.best_score_:.4f}")
best_model = grid_search.best_estimator_
test_accuracy = best_model.score(X_test, y_test)
print(f"Test set accuracy with best model: {test_accuracy:.4f}")
# Plot the results
results = grid_search.cv_results_
n_estimators_values = results['param_classifier__n_estimators'].data.astype(int) # Ensure numeric type for plotting
plt.figure(figsize=(10, 6))
plt.plot(n_estimators_values, results['mean_train_score'], label='Mean Train Score', marker='o')
plt.fill_between(n_estimators_values,
results['mean_train_score'] - results['std_train_score'],
results['mean_train_score'] + results['std_train_score'],
alpha=0.1, color='blue')
plt.plot(n_estimators_values, results['mean_test_score'], label='Mean Validation Score (CV)', marker='s')
plt.fill_between(n_estimators_values,
results['mean_test_score'] - results['std_test_score'],
results['mean_test_score'] + results['std_test_score'],
alpha=0.1, color='orange')
# Highlight the best n_estimators
best_n_estimators = grid_search.best_params_['classifier__n_estimators']
plt.axvline(best_n_estimators, linestyle='--', color='red', label=f'Best n_estimators: {best_n_estimators}')
plt.title('GridSearchCV for n_estimators (RandomForestClassifier)')
plt.xlabel('Number of Estimators (n_estimators)')
plt.ylabel('Accuracy')
plt.legend()
plt.grid(True)
plt.xticks(n_estimators_values) # Ensure all tried values are shown as ticks
plt.tight_layout()
plt.show()Ausgabe
Starting GridSearchCV...
Fitting 5 folds for each of 8 candidates, totalling 40 fits
GridSearchCV finished.
Best parameters found: {'classifier__n_estimators': 200}
Best cross-validation accuracy: 0.9689
Test set accuracy with best model: 0.9655
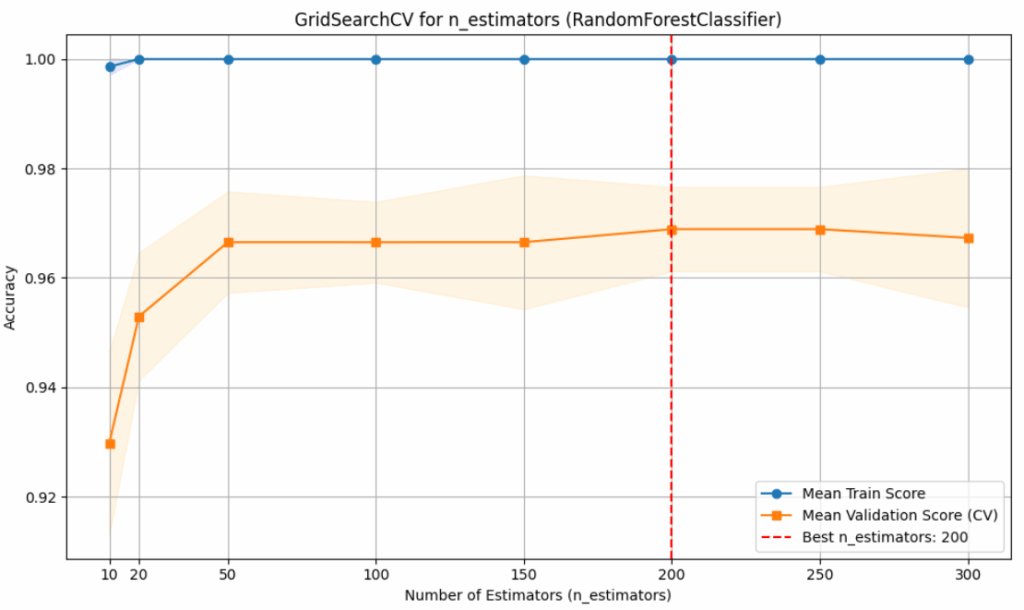
Die blaue Kurve, die den mittleren Trainings-Score („Mean Train Score“) darstellt, erreicht schnell eine Genauigkeit von 1,00 und verbleibt dort über den gesamten Bereich der getesteten n_estimators-Werte. Die orangefarbene Kurve zeigt den mittleren Validierungs-Score aus der Kreuzvalidierung („Mean Validation Score (CV)“). Dieser Validierungs-Score steigt zunächst mit zunehmender Anzahl an Schätzern deutlich an, von etwa 0,93 bei n_estimators=10 auf über 0,965 bei n_estimators=50. Danach flacht der Anstieg ab, und der Score erreicht sein Maximum bei etwa n_estimators=200 mit einem Wert von knapp unter 0,97. Die hellorange schattierte Fläche um die Validierungskurve zeigt die Varianz der Validierungsergebnisse über die verschiedenen Folds der Kreuzvalidierung. Die rot gestrichelte vertikale Linie bei n_estimators=200 markiert den als optimal identifizierten Wert, bei dem die beste Validierungsgenauigkeit erzielt wurde. Damit ist der optimale Wert für n_estimators gefunden und ein entsprechendes Modell trainiert.
Schritt 4: Evaluation des Modells
Der folgende Python-Code dient der Evaluation eines trainierten Machine-Learning-Modells, auf dem Testdatensatz. Zunächst werden mit best_model.predict(X_test) Vorhersagen für die Klassenlabels (y_pred) und mit best_model.predict_proba(X_test) die Wahrscheinlichkeiten für jede Klasse (y_pred_proba) für die Testdaten generiert. Anschließend wird die Leistung des Modells bewertet. Die Gesamtgenauigkeit wird mittels accuracy_score berechnet, indem die tatsächlichen Testlabels mit den vorhergesagten Labels verglichen werden.
# Make Predictions on the Test Set
y_pred = best_model.predict(X_test)
y_pred_proba = best_model.predict_proba(X_test)
# Evaluate the Model
accuracy = accuracy_score(y_test, y_pred)
print(f"\nAccuracy on the test set: {accuracy:.4f}")
print("\nClassification Report:")
print(classification_report(y_test, y_pred)) # target_names can be added if you have them
print("\nConfusion Matrix:")
print(confusion_matrix(y_test, y_pred))Ausgabe:
Accuracy on the test set: 0.9655
Classification Report:
precision recall f1-score support
0_0 0.99 0.96 0.98 1093
127_1 0.93 0.97 0.95 1001
127_2 0.96 0.93 0.94 816
19_1 0.98 0.97 0.98 1059
19_2 0.97 0.98 0.98 1051
accuracy 0.97 5020
macro avg 0.97 0.96 0.96 5020
weighted avg 0.97 0.97 0.97 5020
Confusion Matrix:
[[1054 25 10 4 0]
[ 6 975 20 0 0]
[ 5 54 757 0 0]
[ 0 0 0 1030 29]
[ 3 0 0 17 1031]]
Die Ausgabe zeigt hier eine Genauigkeit von 0.9655, was bedeutet, dass das Modell etwa 96,55% der Instanzen im Testdatensatz korrekt klassifiziert hat. Zusätzlich wird ein detaillierter Klassifikationsbericht erstellt und ausgegeben. Dieser Bericht liefert für jede der fünf Klassen die Metriken Präzision (precision), Sensitivität (recall) und F1-Score, sowie die Anzahl der tatsächlichen Instanzen pro Klasse (support). Die Präzision gibt an, wie viele der als eine bestimmte Klasse vorhergesagten Instanzen tatsächlich zu dieser Klasse gehörten. Die Sensitivität misst, wie viele der tatsächlichen Instanzen einer Klasse korrekt als solche erkannt wurden. Der F1-Score ist das harmonische Mittel aus Präzision und Sensitivität. Der Bericht enthält auch Durchschnittswerte, die eine Gesamtbewertung über alle Klassen hinweg ermöglichen, wobei der gewichtete Durchschnitts-F1-Score bei 0.97 liegt.
Zuletzt wird eine Confusion Matrix ausgegeben. Diese Matrix enthält die Übereinstimmung zwischen den tatsächlichen und den vorhergesagten Klassen in tabellarischer Form. Die Confusion Matrix kann man auch grafisch ausgeben.
unique_values_sum2, counts = np.unique(windows_y_df_sum2, return_counts=True)
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=unique_values_sum2)
# Plotting
# To plot normalized confusion matrix (percentages)
# normalize='true' normalizes over the true conditions (rows)
# normalize='pred' normalizes over the predicted conditions (columns)
# normalize='all' normalizes over all population
disp_normalized = ConfusionMatrixDisplay.from_predictions(
y_test,
y_pred,
display_labels=unique_values_sum2,
cmap=plt.cm.Blues,
normalize='true', # 'true', 'pred', or 'all'
values_format='.2f' # Format for floating point numbers
)
disp_normalized.ax_.set_title("Normalized Confusion Matrix (by True Class)")
plt.show()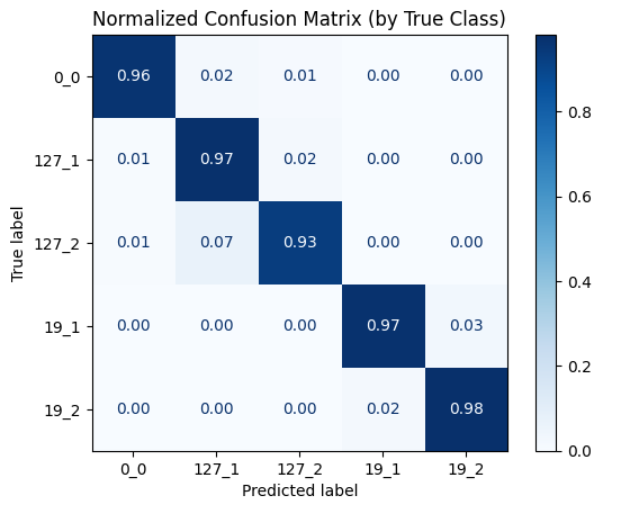
Die vertikale Achse zeigt die wahren Labels, während die horizontale Achse die vom Modell vorhergesagten Labels für dieselben Klassen darstellt. Man erkennt eine sehr gute Klassifikationsleistung, da die diagonalen Elemente, die von oben links nach unten rechts verlaufen und den Anteil der korrekt klassifizierten Instanzen für jede Klasse anzeigen, überwiegend hoch sind. Die meisten Fehler treten bei der Verwechslung zwischen den Klassen 127_2 und 127_1 auf. Das kann aber auch auf schlecht gelabelte Daten hinweisen, da 127_1 und 127_2 die beiden Teilbewegungen der Liegestütze sind. Eine Ähnlicher Fehler tritt auch bei den Bizeps-Curls auf aber der Fehler ist hier deutlich geringer.
Im folgenden Codeabschnitt wird eine 10-fache Kreuzvalidierung durchgeführt. Die Kreuzvalidierung liefert eine Reihe von Bewertungsergebnissen, für jede der zehn Durchläufe einen Wert. Aus den Ergebnissen wird der Durchschnittswert berechnet und die einzelnen Bewertungsergebnisse der Kreuzvalidierungsdurchläufe ausgegeben, gefolgt von dem berechneten durchschnittlichen Bewertungsergebnis.
# Cross-Validation durchführen (5-Fold)
scores = cross_val_score(best_model, windows_X_df_sum2_flat, windows_y_df_sum2, cv=10)
mean_score = scores.mean()
# Ergebnisse anzeigen
print(f"Cross-Validation Scores: {scores}")
print(f"Durchschnittlicher Score: {mean_score:.4f}")Ausgabe:
Cross-Validation Scores: [0.9888535 0.99203822 0.96656051 0.99840764 0.99521531 0.99521531
0.99362041 0.99521531 0.97767145 0.99521531]
Durchschnittlicher Score: 0.9898
Die Cross-Validation Ergebnisse können auch visuell dargestellt werden.
plt.figure(figsize=(8, 4))
plt.plot(range(1, scores.shape[0]+1), scores, marker='o', linestyle='-')
plt.axhline(y=mean_score, color='r', linestyle='--', label=f'Mean Score: {mean_score:.4f}')
plt.title('Cross-Validation Scores pro Fold')
plt.xlabel('Fold')
plt.ylabel(f'Score (Mean={mean_score:.3f})')
plt.ylim(0.95, 1.01)
plt.grid(True)
plt.show()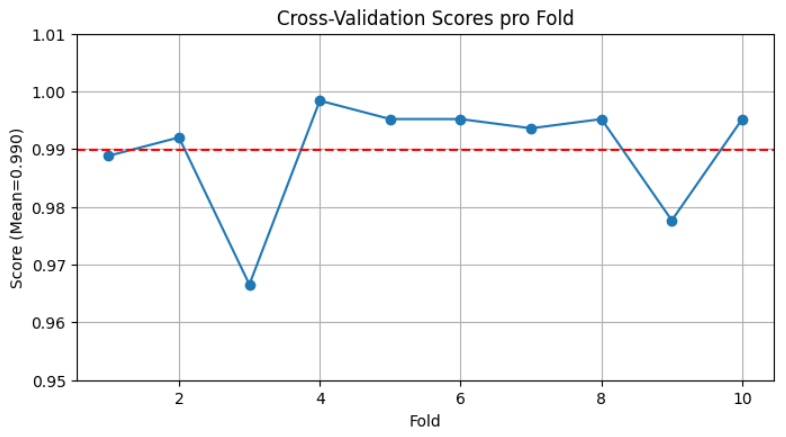
Das Diagramm stellt die Ergebnisse einer Kreuzvalidierung grafisch dar. Auf der horizontalen Achse, beschriftet mit „Fold“, sind die zehn einzelnen Durchläufe der Kreuzvalidierung aufgetragen. Die vertikale Achse, benannt mit „Score (Mean=0.990)“, zeigt den jeweiligen Bewertungsmaßstab, der Werte zwischen 0.95 und 1.01 annimmt.
Der Score im ersten Fold liegt knapp unter 0.99, steigt im zweiten Fold leicht darüber an und fällt im dritten Fold deutlich auf einen Wert um 0.967 ab. Im vierten Fold erreicht der Score seinen höchsten Wert von annähernd 0.999. In den Folds fünf bis acht bewegen sich die Scores relativ konstant um 0.995. Ein erneuter, wenn auch weniger starker Abfall ist im neunten Fold zu erkennen, wo der Score auf etwa 0.978 sinkt, bevor er im zehnten Fold wieder auf einen Wert um 0.995 ansteigt.
Zusätzlich ist eine rote, gestrichelte horizontale Linie bei einem Score-Wert von exakt 0.990 eingezeichnet. Diese Linie repräsentiert den Durchschnittswert der Scores über alle Folds.
Schritt 5: Feature Importance
Die Feature Importance hilft dabei, die innere Funktionsweise eines trainierten Modells zu beschreiben. Man greift hier auf eine Eigenschaft des trainierten Random Forest zu, der die Eigenschaft feature_importances_ besitzt. In der feature_importances_ Variable wird während des Trainings eine Rangliste der Features erstellt. Sie enthält für jedes einzelne Features, das für das Training verwendet wurde, eine numerische Bewertung. Die Feature Importance kann dabei Helfen, Erkenntnisse aus den Daten zu gewinnen, die zu einem besseren Verständnis der Daten führen und dementsprechend auch Hinweise darauf geben, wie man sein System weiter verbessern oder Fehler beheben kann.
Die Feature Importance der IMU Daten kann man sich mit folgendem Code-Fragement anzeigen lassen.
# Feature Importances (optional, aber eine Stärke von Random Forests)
importances = best_classifier.feature_importances_
# feature_names = np.array([f"{i+1}" for i in range(windows_X_df_sum2_flat.shape[1])])
sorted_indices = np.argsort(importances)[::-1]
plt.figure(figsize=(16,8))
plt.title("Feature Importances")
plt.bar(range(windows_X_df_sum2_flat.shape[1]), importances[sorted_indices], align="center")
# plt.xticks(range(windows_X_df_sum2_flat.shape[1]), np.array(feature_names)[sorted_indices], rotation=45)
plt.tight_layout()
plt.show()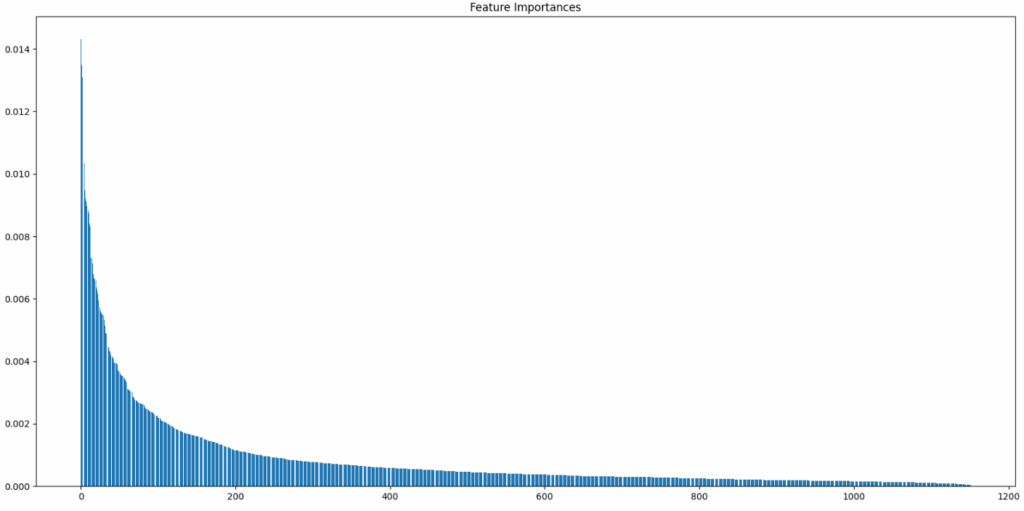
Wie man in dem Balkendiagramm sehen kann gibt es nur sehr wenige Features in dem 1152×1 Feature-Vektor, die großen Einfluss (> 1%) auf das Modell haben, während es sehr viele Features gibt, die geringen Einfluss auf das Modell haben (< 0.2%). Welche das genau sind lässt sich in dem Diagramm mit 1152 Balken leider nicht genau sagen. Spannend könnte sein, ob eher die imu Accelerometer oder die Gyro Daten des IMU Sensors relevant sind und ob die relevanten Features eher in der Mitte der Sliding Windows oder am Rand liegen. Um das herauszufinden, kann man das folgende Code-Snippet verwenden, dass 6 Balkendiagramme zeichnet (AX, AY, AZ, GX, GY und GZ) und die Position der Features nicht nach Einfluss auf das Modell sortiert, so dass man besser verstehen kann, welche Features sich auf das Modell auswirken.
# Liste der Features und ihre Start-Offsets im 'importances'
feature_info = {
"AX": 0,
"AY": 1,
"AZ": 2,
"GX": 3,
"GY": 4,
"GZ": 5,
}
WINDOW_SIZE = 20
# Funktion zum Plotten eines einzelnen Features
def plot_feature_importance(ax, feature_data, feature_name, window_size):
"""
Plottet die Importance-Werte und den gleitenden Durchschnitt für ein Feature.
"""
# Berechnung des gleitenden Durchschnitts
feature_series = pd.Series(feature_data)
moving_average = feature_series.rolling(window=window_size, center=True, min_periods=1).mean()
# Balkendiagramm für einzelne Importance-Werte
color_bar = 'tab:blue'
ax.set_xlabel(f"Features (Indizes 0 bis {feature_data.shape[0]-1})") # X-Achse nur bei Bedarf
ax.set_ylabel("Importance (Einzeln)", color=color_bar)
ax.bar(range(feature_data.shape[0]), feature_data, align="center", width=1.0, color=color_bar, alpha=0.6, label="Einzelne Importance")
ax.tick_params(axis='y', labelcolor=color_bar)
# Liniendiagramm für gleitenden Durchschnitt auf einer zweiten Y-Achse
ax_twin = ax.twinx()
color_line = 'tab:red'
ax_twin.set_ylabel(f'Gleitender Durchschnitt (Fenster={window_size})', color=color_line)
ax_twin.plot(range(feature_data.shape[0]), moving_average, color=color_line, linestyle='-', linewidth=2, label=f'Gleitender Durchschnitt')
ax_twin.tick_params(axis='y', labelcolor=color_line)
ax.set_title(f"Feature {feature_name} Importance")
# Manuelle Erstellung der Legende
lines, labels = ax.get_legend_handles_labels()
lines2, labels2 = ax_twin.get_legend_handles_labels()
ax_twin.legend(lines + lines2, labels + labels2, loc='upper right')
# --- Erstellen der Subplots ---
# 6 Subplots, also z.B. 3 Zeilen und 2 Spalten
fig, axes = plt.subplots(nrows=3, ncols=2, figsize=(16, 18))
axes = axes.flatten() # Macht aus dem 2D-Array von Achsen ein 1D-Array für einfache Iteration
feature_names = list(feature_info.keys())
for i, feature_name in enumerate(feature_names):
offset = feature_info[feature_name]
current_feature_importance = importances[offset::6]
# Plot für das aktuelle Feature auf der entsprechenden Achse
plot_feature_importance(axes[i], current_feature_importance, feature_name, WINDOW_SIZE)
# X-Achsenbeschriftung nur für die unterste Reihe von Subplots, um Redundanz zu vermeiden
if i < len(feature_names) - 2 : # Alle außer den letzten beiden (unterste Reihe)
axes[i].set_xlabel("")
else:
axes[i].set_xlabel(f"Feature-Indizes (0 bis {current_feature_importance.shape[0]-1})")
fig.suptitle("Feature Importance mit gleitendem Durchschnitt für 6-Achsen IMU Sensor", fontsize=16)
# rect=[left, bottom, right, top] -> Platz für suptitle schaffen
fig.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()Der Code erzeugt folgende Diagramme:
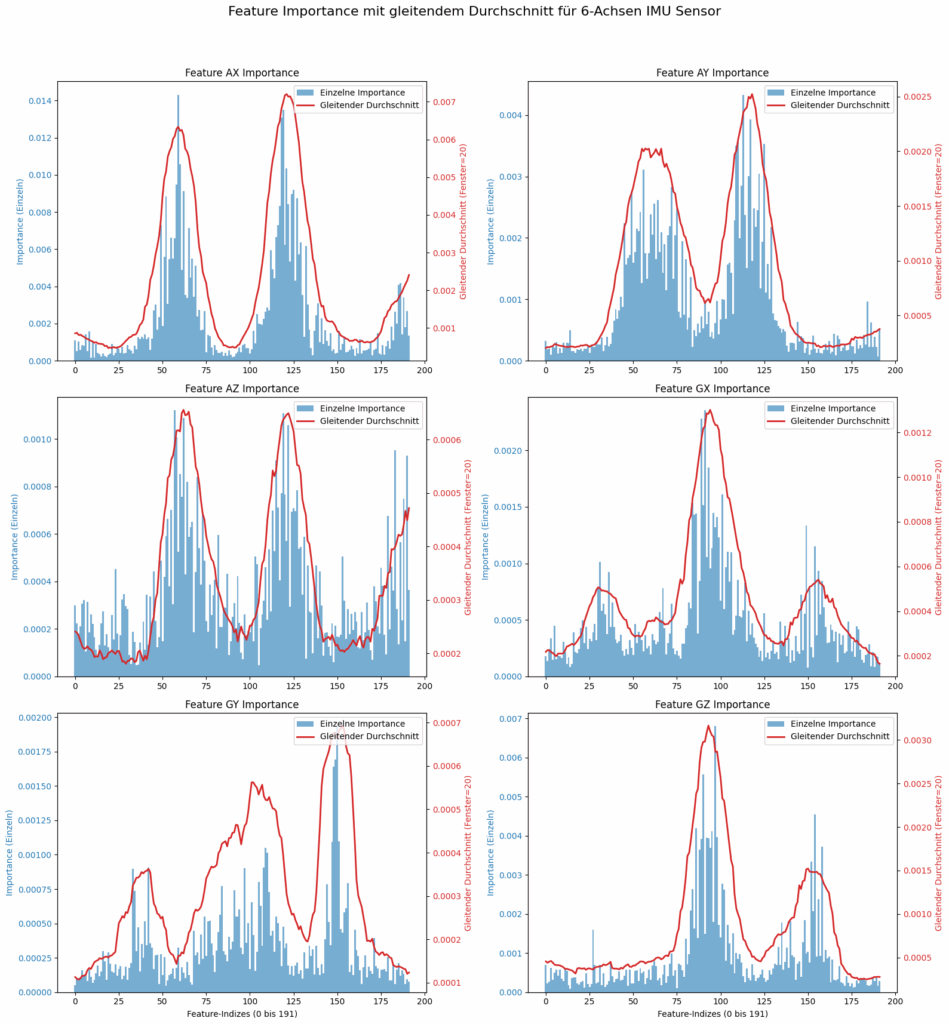
Das Bild zeigt die Analyse der Merkmalswichtigkeit für die IMU Sensordaten. Die Darstellung zeigt sechs Diagramme, von denen sich jedes auf eine spezifische Achse des 6-Achsen-IMU-Sensors bezieht: die Beschleunigungsachsen AX, AY, AZ und die Gyroskopachsen GX, GY, GZ. In jedem Diagramm wird die Wichtigkeit von Merkmalen entlang einer horizontalen Achse dargestellt die sich über das vorgegebene Sliding Window erstreckt, das 192 Features pro Sensor enthält.
Es gibt zwei überlagerte Darstellungen: Ein blaues Balkendiagramm visualisiert die „Einzelne Feature-Importance“ für jedes einzelne Feature und eine durchgehende rote Linie, die den „Gleitender Durchschnitt“ mit einer WINDOW_SIZE (Fenstergröße) von 20 darstellt. Diese geglättete Linie hilft dabei, die zugrundeliegenden Trends und die Bereiche mit der höchsten kumulativen Wichtigkeit leichter zu erkennen. Jedes Diagramm verwendet zwei vertikale Achsen. Die linke für die einzelnen Wichtigkeitswerte und die rechte, farblich passende, für die Werte des gleitenden Durchschnitts.
In den Diagrammen, wie bei AX, AY und AZ lassen sich deutlich zwei Hauptbereiche mit hoher Wichtigkeit erkennen, die als zwei große „Hügel“ in der roten Linie erscheinen. Wobei die Skalierung des AX Diagramms mit einem Max. von 1.4% max. deutlich über den anderen beiden Diagrammen (AY = 0.4% max. und AZ = 0.1% max.) liegt. Die Diagramme GX, GY und GZ haben eine andere Verteilung der Feature-Importance. Hier gibt es bei GX und GY jeweils 3 Hauptbereiche, wobei jeweils der mittlere die höchste Wichtigkeit besitzt. Der GZ Feature Block hat wieder nur 2 Hauptbereiche, von denen sich der höhere in der Mitte befindet und der niedrigere auf der rechten Seite. GZ hat mit einem max. von 0.7% auch den höchsten Peek im Vergleich zu den anderen Gyroskopachsen die GX = 0.2% max. und GY = 0.2% max. einen deutlich geringeren Anteil besitzen.
Insgesamt verdeutlicht die Visualisierung, welche Zeitabschnitte oder Merkmale innerhalb der Sensordaten für jede Achse die größte Bedeutung haben. Es ist deutlich zu erkennen, dass der Beschleunigungssensor wichtiger für die Unterscheidung der beiden Übungen ist und dass der AX Sensor mit einem max. von 1.4% bei weitem den größten Anteil daran hat. Es ist auch deutlich zu erkennen, dass die Randbereiche der Sliding Windows einen geringeren Einfluss auf das Modell haben was darauf hindeutet, dass die Sliding Windows groß genug gewählt sind.
Fazit zur 30-Tage scikit-learn Challenge
Die 30-tägige scikit-learn Challenge war ein interessantes Experiment das mir viele praktische Einblicke in die wichtigste ML-Bibliothek in Python gewährt hat. Angefangen bei der Installation, dem Laden von Daten und dem Trainieren eines ersten einfachen Modells über verschiedene Konzepte wie der Train-Test-Split und Modellbewertung habe ich viele verschiedene KI-Algorithmen bearbeitet. Z.B. k-Nearest Neighbors, Random Forest, Gradient Boosting, Support Vector Machines. Über das reine Anwenden von Algorithmen hinaus waren die zentralen Punkte, die Pipelines, die Datenvorbereitung und die Evaluation von Modellen und Hyperparametern mit Hilfe verschiedener Metriken. Besonders spannend fand ich auch das Thema Feature-Importance.
Alles in allem habe ich gelernt, dass Machine-Learning viel mehr ist als Gen-AI oder Deep-Learning und dass man selbst mit limitierten Ressourcen gute Ergebnisse erzielen kann, wenn man nicht einfach stupf auf Deep-Learning setzt und sich mit dem eigentlichen Problem auseinandersetzt und die richtigen Komponenten zusammenfügt.
Tag 30 fasst noch mal den gesamte End-to-End-Prozess des maschinellen Lernens zusammen. Von der Datenanalyse und dem Feature Engineering über das Training bis zur Validierung und der Feature-Importance. Das abschließende Mini-Projekt an Tag 30 war die perfekte Gelegenheit, alle erlernten Fähigkeiten zu kombinieren und das gewonnene Wissen zu festigen.
Ehrlicherweise muss ich aber zugeben, dass ich an „Tag 30“ nicht nur an einem Tag gearbeitet habe. Mir war klar, dass ich das nicht an einem Tag schaffe, daher habe ich schon an den vorherigen Tagen immer mal wieder ein wenig an „Tag 30“ gearbeitet um auch pünktich fertig zu werden. So weit so gut. Mal sehen, welches Thema ich mir als nächstes vorknöpfe …..
