TODO für Tag 4
- k-Nearest Neighbors versetehen
- k-Nearest Neighbors Classifier
- k-Nearest Neighbors Regression
- Überprüfen, wie sich der k-Wert auf Accuracy auswirkt
k-Nearest Neighbors
k-Nearest Neighbors ist ein einfaches, Klassifikationsverfahren mit dem man einen neuen Datenpunkt basierend auf seinen nächsten Nachbarn klassifiziert. Dabei wird die Klassenzugehörigkeit durch Mehrheitsentscheidung der Nachbarn bestimmt. Für jede Vorhersage wird die Distanz zu allen Trainingspunkten berechnet, um die k nächsten Nachbarn zu finden. Das ist jedoch bei großen Datensätzen sehr rechenintensiv (O(n) pro Vorhersage). K-NN sind auch als „lazy learner“ bekannt, da es keine Funktion aus den Trainingsdaten lernt, sondern sich stattdessen den Trainingsdatensatz „merkt“. Deshalb gibt es bei K-NN auch keine Trainingszeit.
Es gibt auch eine k-Nearest Neighbors Regression. Bei der Regression wird der Durchschnitt der Nachbarn genommen. In scikit-learn gibt es die beiden Nearest Neighbors-Regressoren KNeighborsRegressor und RadiusNeighborsRegressor. Der Hauptunterschied zwischen den Beiden liegt in der Art und Weise, wie sie Nachbarn für die Regression bestimmen.
| Merkmal | KNeighborsRegressor | RadiusNeighborsRegressor |
|---|
| Nachbarschaftsdefinition | Feste Anzahl von Nachbarn (k) | Alle Nachbarn innerhalb eines Radius |
| Parameter | n_neighbors | radius |
| Empfindlichkeit | Kann empfindlich gegenüber Ausreißern sein | Robuster gegenüber Ausreißern |
| Handhabung leerer Nachbarschaften | Immer k Nachbarn vorhanden | Kann keine Vorhersage treffen, wenn keine Nachbarn im Radius |
k-Nearest Neighbors Classifier
Das Folgende Python Skripte trainiert einen KNeighborsClassifier auf den Iris Datensatz. Dabei wird der Iris Datensatz mit der train_test_split Funktion in die Train und Test Daten aufgeteilt und 50% der Daten für das Training und 50% für den Test aufgeteilt. Der KNeighborsClassifier wird dann mit den Trainingsdaten trainiert und der accuracy_score der Testdaten ermittelt. Die Anzahl der Nachbarn wird auf 3 beschränkt.
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier, RadiusNeighborsClassifier
from sklearn.metrics import accuracy_score
# Iris-Daten laden
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Daten splitten
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=42)
# Modell instanziieren mit k=3
knn = KNeighborsClassifier(n_neighbors=3)
# Modell trainieren
knn.fit(X_train, y_train)
# Vorhersagen machen
y_pred = knn.predict(X_test)
# Genauigkeit berechnen
accuracy = accuracy_score(y_test, y_pred)
print(f"Genauigkeit mit k=3: {accuracy:.2f}")Die Ausgabe der Genauigkeit ist dann 97%.
Genauigkeit mit k=3: 0.97
Alternativ kann man auch den RadiusNeighborsClassifier verwenden, der als Parameter einen Radius bekommt. Dazu wird einfach nur die Zeile „knn = KNeighborsClassifier(n_neighbors=3)“ durch die Zeile „knn = RadiusNeighborsClassifier(radius=2)“ ersetzt. Für den Radius 2 ergibt sich dann eine Genauigkeit von 91%
Genauigkeit mit k=3: 0.91
Um die Modelle zu optimieren kann man mit den Parametern n_neighbors und radius herumprobieren, bis die Modelle für die Daten optimale Ergebnisse liefern. Mit dem folgenden Skript wird n_neighbors von von 1-20 durchprobiert und die Genauigkeit in einem Plot ausgegeben.
import matplotlib.pyplot as plt
accuracies = []
for k in range(1, 21):
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
acc = accuracy_score(y_test, y_pred)
accuracies.append(acc)
plt.plot(range(1, 21), accuracies, marker='o')
plt.title('k-NN: Genauigkeit für verschiedene k-Werte')
plt.xlabel('Anzahl der Nachbarn k')
plt.ylabel('Genauigkeit')
plt.grid(True)
plt.show()Die Genauigkeit des KNeighborsClassifier mit den Werten 1-20 für n_neighbors.
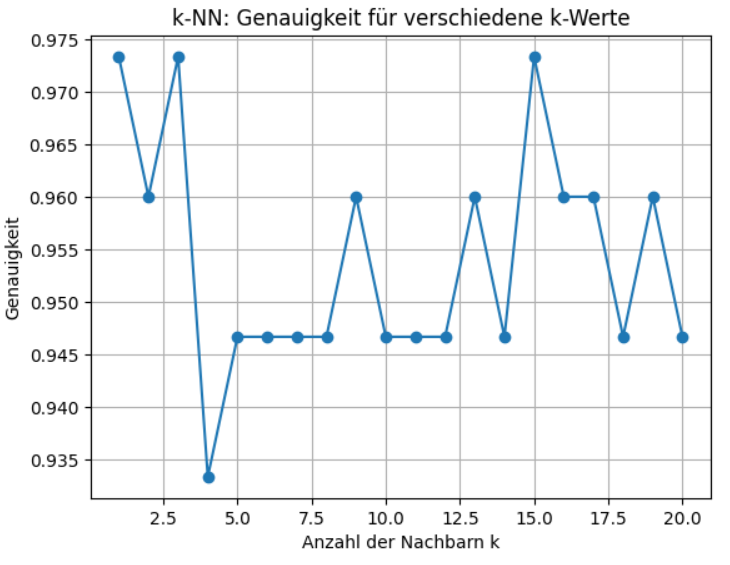
Wie man sieht, ist der KNeighborsClassifier für den Iris Datensatz sehr stabil und die Genauigkeit ist je nach n_neighbors zwischen 93% und 97%.
Das gleiche kann man nun auch für den RadiusNeighborsClassifier mit dem Parameter raduis machen.
import matplotlib.pyplot as plt
accuracies = []
for k in range(2, 11):
knn = RadiusNeighborsClassifier (radius=k)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
acc = accuracy_score(y_test, y_pred)
accuracies.append(acc)
plt.plot(range(2, 11), accuracies, marker='o')
plt.title('RadiusNeighborsClassifier Genauigkeit')
plt.xlabel('Radius')
plt.ylabel('Genauigkeit')
plt.grid(True)
plt.show()Hier sieht die Kurve aber ganz anders aus. Für den radius verwende ich hier eine Range von 2-11. Das Ergebnis sieht dann wie folgt aus:
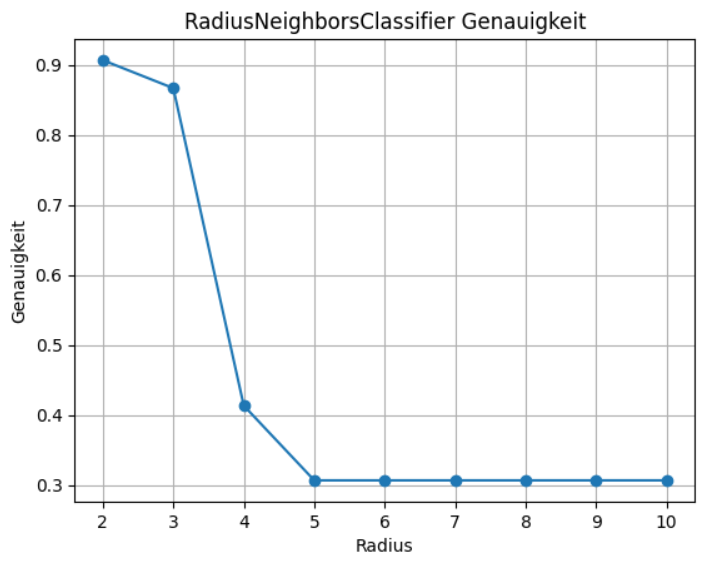
Bei einem Radius von 2 oder 3 ist die Genauigkeit extrem hoch (über 90% bzw. 85%). Ab Radius 4 stürzt die Genauigkeit komplett ab (auf ca. 40%). Ab Radius 5 bis 10 pendelt sich die Genauigkeit auf einem sehr schlechten Niveau bei etwa 30% ein.
- Kleine Radien (2, 3)
Die Nachbarschaft ist klein genug, dass die Punkte tatsächlich zur „richtigen“ Klasse gehören → hohe Genauigkeit. - Größere Radien (ab 4)
Der Radius wird so groß, dass viele Punkte aus anderen Klassen eingeschlossen werden → der Klassifikator verwässert → die Vorhersagen werden unsicher → Accuracy sinkt dramatisch. - Ab Radius 5
Der Radius ist schon so groß, dass fast das gesamte Feature-Space als „Nachbar“ gilt → das Modell verliert jegliche Präzision.
Beim Iris-Datensatz (wenige Punkte, gut separierbare Cluster) zeigt Radius-NN seine Schwächen während der KNeighborsClassifier sehr stabil ist.
Verwendung von KNeighborsRegressor
Der KNeighborsRegressor ist ein einfaches, aber wirkungsvolles Verfahren für Regressionsaufgaben, das auf dem Konzept der „nächsten Nachbarn“ basiert.
Bei einer Vorhersage sucht es die k nächsten Trainingspunkte im Feature-Raum und berechnet den Durchschnitt (oder ein gewichtetes Mittel) ihrer Zielwerte.
Hier ein einfaches Beispiel:
from sklearn.datasets import load_diabetes
from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
# Daten laden
diabetes = load_diabetes()
X = diabetes.data
y = diabetes.target
# Train/Test Split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Feature Skalierung (wichtig für k-NN)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# k-NN Regressor mit 5 Nachbarn
knn_reg = KNeighborsRegressor(n_neighbors=5)
knn_reg.fit(X_train_scaled, y_train)
# Vorhersagen
y_pred = knn_reg.predict(X_test_scaled)
# Bewertung: Mittlerer quadratischer Fehler (MSE)
mse = mean_squared_error(y_test, y_pred)
print(f"MSE auf Testdaten: {mse:.2f}")Ausgabe:
MSE auf Testdaten: 3047.45
Der MSE (Mean Squared Error) ist eine Kennzahl, die misst, wie stark die Vorhersagen eines Modells von den tatsächlichen Zielwerten abweichen. Zur Berechnung des MSE wird für jeden einzelnen Testdatenpunkt wird der absolute Fehler (quadriert damit sich negative und positive Fehler nicht gegenseitig aufheben und große Fehler stärker gewichtet werden) berechnet. Über die Summe der Fehler wird dann der Durchschnitt über alle Fehler gebildet.
MSE Formel:
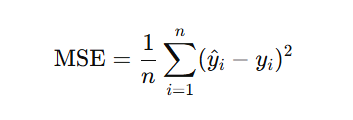

Was bedeutet dein Wert von 3047.45 konkret?
Im Mittel weicht dein k-NN-Modell bei der Vorhersage des Diabetes-Scores um etwa die Quadratwurzel von 3047.45 ab. Die Quadratwurzel von 3047.45 ist ca. 55.22. Im Durchschnitt liegt das Modell bei den Vorhersagen etwa 55 Einheiten daneben. Wenn der tatsächliche Score eines Patienten also z. B. bei 200 liegt, sagt das Modell im Mittel irgendetwas zwischen145 und 255 voraus (±55).
Zusammenfassung:
| Einsatzbereich | Klasse in scikit-learn | Vorgehensweise |
|---|---|---|
| Klassifikation (Kategorievorhersage) | KNeighborsClassifier | Mehrheit der k Nachbarn entscheidet Klasse |
| Klassifikation (Kategorievorhersage) | RadiusNeighborsClassifier | Nachbarn innerhalb eines Radius entscheidet Klasse |
| Regression (kontinuierliche Werte) | KNeighborsRegressor | Durchschnitt der k Nachbarn wird Wert |
