TODO für Tag 7
- Neue Features erzeugen (Polynomiale Features mit PolynomialFeatures)
- Feature Auswahl: Simple Methoden mit SelectKBest
Neue Polynomiale Features mit PolynomialFeatures erzeugen
Mit PolynomialFeatures von sklearn.preprocessing kann man aus bestehenden Features neue Features erzeugen, indem man die bestehenden Features potenziert oder multipliziert. So können komplexere Zusammenhänge zwischen den Features und dem Zielwert abgebildet werden, die mit rein linearen Modellen nicht abgebildet werden können.
Hier ein Beispiel:
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
import pandas as pd
# Beispiel-Daten
X = np.array([[2, 3],
[3, 5],
[5, 7]])
# PolynomialFeatures initialisieren
poly = PolynomialFeatures(degree=2, include_bias=False) # include_bias=False -> keine konstante 1-Spalte
# Transformieren
X_poly = poly.fit_transform(X)
# Ausgabe der neuen Feature-Namen
feature_names = poly.get_feature_names_out(['x1', 'x2'])
# Ergebnis als DataFrame
df = pd.DataFrame(X_poly, columns=feature_names)
print(df)Der Dataframe df enthalt nun folgende Werte
x1 x2 x1^2 x1 x2 x2^2 0 2.0 3.0 4.0 6.0 9.0 1 3.0 5.0 9.0 15.0 25.0 2 5.0 7.0 25.0 35.0 49.0
Durch die Anwendung von PolynomialFeatures bleiben die ursprünglichen Features (x1, x2) erhalten und es werden zusätzliche Features ergänzt. So schafft man neue Feature-Wechselwirkungen, die das Modell evtl. besser nutzen kann.
Hier eine Grafische Darstellung zum besseren Verständnis
import matplotlib.pyplot as plt
# Plotten
df.plot(marker='o')
plt.title('Polynomial Features')
plt.xlabel('Samples')
plt.ylabel('Feature Values')
plt.grid(True)
plt.legend(title='Features')
plt.show()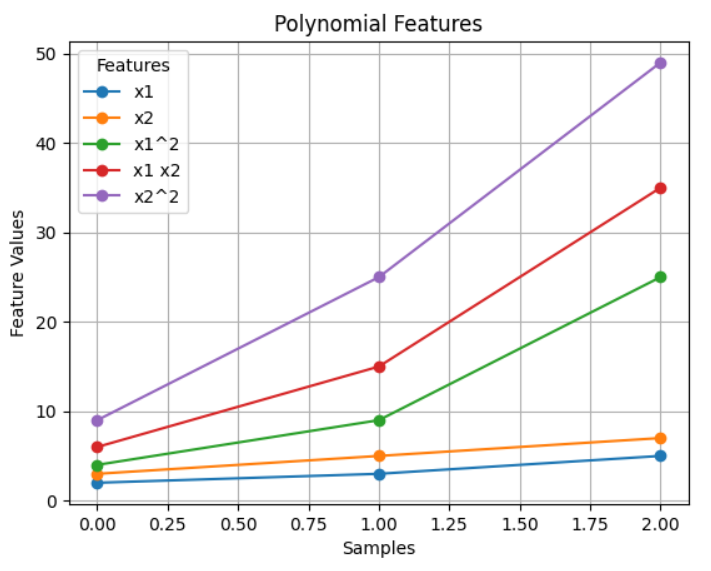
Plotten mit logarithmischer Y-Skalierung
import matplotlib.pyplot as plt
ax = df.plot(marker='o')
ax.set_yscale('log') # <-- Hier wird die Y-Achse logarithmisch gesetzt
plt.title('Polynomial Features (Logarithmische Skalierung)')
plt.xlabel('Samples')
plt.ylabel('Feature Values (log)')
plt.grid(True, which="both", ls="--")
plt.legend(title='Features')
plt.show()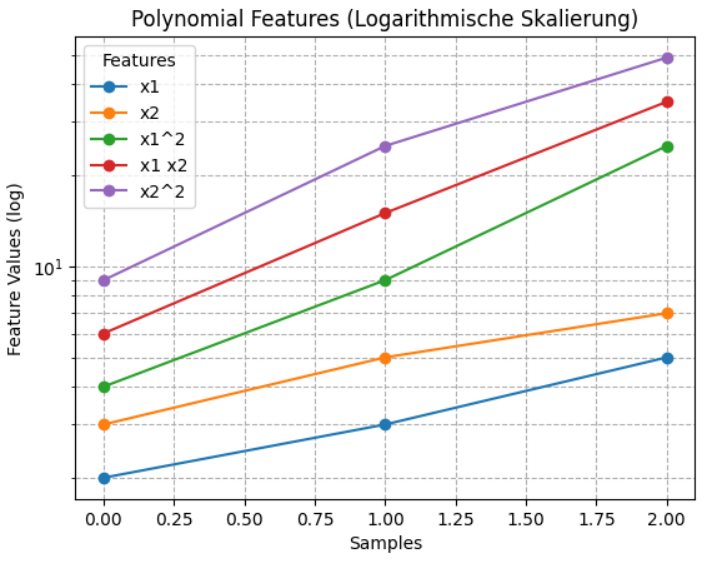
Die Logarithmische Skalierung ist besser, da die Feature-Werte stark unterschiedliche Größenordnungen haben. Dadurch werden Zusammenhänge sichtbar, die in einer linearen Skalierung untergehen würden. Außerdem verhindert sie, dass einzelne große Werte die gesamte Darstellung dominieren und hilft, Trends und Muster klarer zu erkennen.
Feature Auswahl: Simple Methoden mit SelectKBest
SelectKBest ist eine Filtermethode zur Feature-Auswahl. Sie bewertet jedes einzelne Feature unabhängig von den anderen und wählt die K besten Features aus – basierend auf einem statistischen Test.
Beispiel:
from sklearn.datasets import fetch_california_housing
from sklearn.feature_selection import SelectKBest, f_regression
import pandas as pd
# Daten laden
data = fetch_california_housing()
X = data.data
y = data.target
# SelectKBest initialisieren – behalte die 5 besten Features
selector = SelectKBest(score_func=f_regression, k=5)
# Feature Auswahl anwenden
X_selected = selector.fit_transform(X, y)
# Welche Features wurden ausgewählt?
selected_features = selector.get_support(indices=True)
# Ausgabe
print("Ausgewählte Feature-Indizes:", selected_features)
# Optional: Als DataFrame anzeigen
feature_names = data.feature_names
selected_feature_names = [feature_names[i] for i in selected_features]
print("Ausgewählte Feature-Namen:", selected_feature_names)Der Code lädt den California Housing Datensatz und wendet SelectKBest auf die Features an. Dafür wird SelectKBest mit dem statistischen Test f_regression konfiguriert, um die fünf Merkmale auszuwählen, die die stärkste lineare Beziehung zum Zielwert haben.
f_regression ist eine Funktion aus scikit-learn, die für jedes Feature einen linearen Regressions-Test gegen den Zielwert (y) durchführt. Sie berechnet den F-Wert (also das Verhältnis von erklärter Varianz zu nicht erklärter Varianz) und den p-Wert (die Wahrscheinlichkeit, dass das Ergebnis durch Zufall entstanden ist). Dazu wird für jedes Feature eine lineare Regression durchgeführt, um zu sehen, wie stark das Feature alleine den Zielwert erklären kann.
Mit selector.fit_transform() wird die ursprüngliche Eingabematrix immer weiter reduziert, bis nur noch die besten fünf Features enthalten sind.
Danach wird mit selector.get_support() ermittelt, welche Features ausgewählt wurden, und es wird zusätzlich eine Zuordnung der gewählten Indizes zu den ursprünglichen Feature-Namen erstellt. Die Ausgabe des Skripts sieht dann wie folgt aus:
Ausgewählte Feature-Indizes: [0 1 2 3 6]
Ausgewählte Feature-Namen: ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Latitude']
Von den ursprünglich 8 Features des California housing dataset sind also die 5 Features MedInc, HouseAge, AveRooms, AveBedrmsm und Latitude geblieben. Die anderen 3 Features Population, AveOccup und Longitude sind bei der Feature Auswahl entfallen.
Um nun herauszufinden, um wie viele Features man reduzieren kann ohne das die Qualität des Modells so weit absinkt, dass sie unter die Mindestanforderungen fällt, kann man die Anzahl der Features immer weiter reduzieren mit dem reduzierten Feature Set wieder ein Modell trainieren. Das geht dann z.B. wie folgt:
from sklearn.datasets import fetch_california_housing
from sklearn.feature_selection import SelectKBest, f_regression
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score, mean_squared_error
import matplotlib.pyplot as plt
import numpy as np
# Daten laden
data = fetch_california_housing()
X = data.data
y = data.target
feature_names = data.feature_names
# Daten splitten
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Listen zum Speichern der Ergebnisse
num_features_list = []
r2_scores = []
mse_scores = []
# Modelle trainieren (k = 8 bis 1)
for k in range(8, 0, -1):
if k == 8:
# Alle Features verwenden
X_train_k = X_train
X_test_k = X_test
else:
# Feature Auswahl mit SelectKBest
selector = SelectKBest(score_func=f_regression, k=k)
selector.fit(X_train, y_train)
X_train_k = selector.transform(X_train)
X_test_k = selector.transform(X_test)
# Modell trainieren
model = LinearRegression()
model.fit(X_train_k, y_train)
# Vorhersage
y_pred = model.predict(X_test_k)
# Scores berechnen
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
# Ergebnisse speichern
num_features_list.append(k)
r2_scores.append(r2)
mse_scores.append(mse)
# Ergebnisse plotten
fig, ax1 = plt.subplots()
color = 'tab:blue'
ax1.set_xlabel('Anzahl der Features')
ax1.set_ylabel('R^2 Score', color=color)
ax1.plot(num_features_list, r2_scores, marker='o', color=color, label='R^2 Score')
ax1.tick_params(axis='y', labelcolor=color)
ax1.invert_xaxis() # Größte Anzahl (8) links, 1 rechts
# Zweite Y-Achse für MSE
ax2 = ax1.twinx()
color = 'tab:red'
ax2.set_ylabel('MSE', color=color)
ax2.plot(num_features_list, mse_scores, marker='x', linestyle='--', color=color, label='MSE')
ax2.tick_params(axis='y', labelcolor=color)
# Titel und Grid
plt.title('Modellleistung vs. Anzahl der Features (California Housing)')
fig.tight_layout()
plt.grid(True)
plt.show()Der Python-Code führt eine einfache Analyse durch, wie sich die Leistung eines linearen Regressionsmodells auf dem California Housing Dataset ändert, wenn unterschiedlich viele Features (Merkmale) für das Training des Modells verwendet werden. Der Code testet die Performance eines linearen Regressionsmodells systematisch, indem es jeweils mit 8, 7, 6, …, 1 Features trainiert, wobei die Features basierend auf ihrer Korrelation mit der Zielvariablen ausgewählt werden, und die Ergebnisse (R² und MSE) visuell darstellt, um zu zeigen, wie sich die Modellgüte mit der Anzahl der verwendeten Features verändert. Die Ausgabe zeigt, dass sich die Modellleistung ab einer Anzahl von 5 Fetures deutlich verschlechtert.
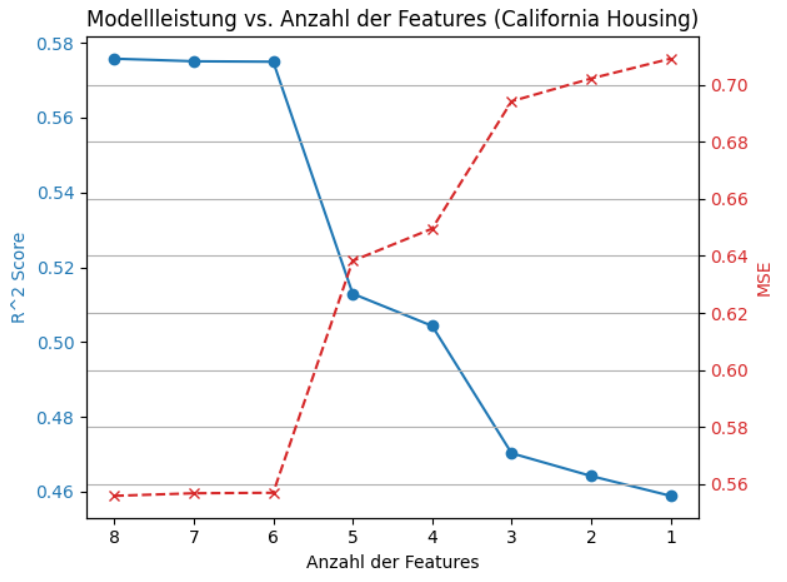
Diese Grafik zeigt sehr deutlich, wie schnell die Modellqualität fällt, wenn man Features entfernt, ob weniger Features vielleicht fast gleich gut sind wie alle Features und ab welchem Punkt das Modell richtig einbricht.
Eine Reduktion mit SelectKBest auf die wichtigsten Features spart Komplexität, aber zu starke Reduktion führt zu deutlich schlechterer Vorhersagequalität. Es ist also immer ein abwägen nötig und es ist zwingend erforderlich, sich intensiv mit den Features zu befassen, bevor man eine Feature Selektion mit SelectKBest in Erwägung zieht.
