TODO für Tag 5
- Lineare Regression verstehen und implementieren
- Interpretation der Koeffizienten
- Vorhersagen und Fehlermaße (MSE, R2)
Lineare Regression verstehen und implementieren
Das Ziel der linearen Regression ist es eine Gerade (oder Hyperplane in mehreren Dimensionen) zu finden, die den Zusammenhang zwischen denFeatures und einem Label am besten wiedergibt.scikit-learn stellt mit LinearRegression eine Klasse zur Verfügung, das diese Gewichte über Least Squares (kleinste Fehlerquadrate) optimiert.
Hier ist ein kleines Beispiel mit künstlichen Daten:
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# Beispiel-Daten (Feature: X, Target: y)
X = np.array([[1], [2], [3], [4], [5]]) # Features
y = np.array([2, 4, 5, 4, 5]) # Label
model = LinearRegression()
model.fit(X, y)
# Modell-Parameter
print("Steigung (Koeffizient):", model.coef_[0])
print("Achsenabschnitt (Bias):", model.intercept_)
# Vorhersage
X_test = np.array([[6], [7]])
y_pred = model.predict(X_test)
print("Vorhersagen für X_test:", y_pred)
# Visualisierung
plt.scatter(X, y, color='blue', label="Trainingsdaten")
plt.plot(X, model.predict(X), color='red', label="Regression")
plt.scatter(X_test, y_pred, color='green', label="Vorhersagen")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
plt.title("Lineare Regression Beispiel")
plt.show()Der Python-Code zeigt ein Beispiel für eine lineare Regression, bei der mit scikit-learn ein Modell auf kleinen Trainingsdaten trainiert wird. Zunächst werden die Featues (X) und die Label (y) als Arrays definiert, danach wird ein LinearRegression-Modell erstellt und mit den Trainingsdaten trainiert. Anschließend werden die erlernte Steigung und der Achsenabschnitt ausgegeben. Das Modell nutzt die gelernten Parameter, um Vorhersagen für neue Eingabewerte zu treffen.
Das Skript gibt folgenden Informationen über die Modellparameter und die Grafik aus.
Steigung (Koeffizient): 0.6 Achsenabschnitt (Bias): 2.2 Vorhersagen für X_test: [5.8 6.4]
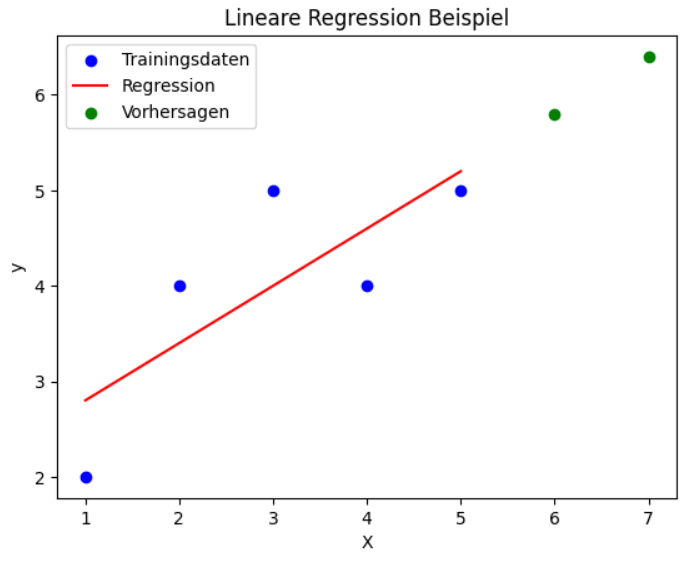
Die blauen Punkte repräsentieren die Trainingsdaten, die eine gewisse Streuung um eine gedachte Gerade aufweisen. Die rote Linie ist die ermittelte Regressionsgerade, die den Trend der Trainingsdaten bestmöglich beschreibt. Zusätzlich sieht man zwei grüne Punkte rechts im Diagramm, die die Vorhersagen des Modells für die Testdaten darstellen.
Interpretation der Koeffizienten
In dem Beispiel sind die Koeffizienten die Werte, die das Verhalten der gelernten linearen Funktion bestimmen.
- Steigung (Koeffizient
coef_)
Gibt an, wie stark sich der Zielwertyverändert, wenn sich der EingabewertXum eine Einheit erhöht. In deinem Fall ist der Wert der Steigung etwa 0,6. Das bedeutet: Wenn sichXum 1 erhöht, steigt die Vorhersageyim Durchschnitt um etwa 0,6. - Achsenabschnitt (Bias
intercept_)
Gibt den Wert vonyan, wennX = 0ist. Also, der Startpunkt der Regressionsgeraden auf der y-Achse. In dem Beispiel liegt dieser Bias bei etwa 2,2. Das heißt: Wenn X = 0 (was außerhalb der Trainingsdaten liegt), wird das Modell einen y-Wert von 2,2 vorhersagen.
Also steigt y um 0,6 wenn X um 1 steigt, und wenn X = 0, liegt y bei 2,2.
Vorhersagen und Fehlermaße (MSE, R2)
Zum Verständnis von Vorhersagen und Fehlermaße habe ich eine erweitere Version des Beispiels, erstellt, in dem der Mean Squared Error (MSE) und das Bestimmtheitsmaß R² (R2-Score) berechnet wird.
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
# Beispiel-Daten (Feature: X, Target: y)
X = np.array([[1], [2], [3], [4], [5]]) # Feature muss 2D sein
y = np.array([2, 4, 5, 4, 5]) # Zielwerte
# Modell erstellen
model = LinearRegression()
# Modell trainieren
model.fit(X, y)
# Modell-Parameter
print("Steigung (Koeffizient):", model.coef_[0])
print("Achsenabschnitt (Bias):", model.intercept_)
# Vorhersagen auf Trainingsdaten
y_train_pred = model.predict(X)
# Fehlermaße
mse = mean_squared_error(y, y_train_pred)
r2 = r2_score(y, y_train_pred)
print("Mean Squared Error (MSE):", mse)
print("R2-Score:", r2)
# Neue Vorhersagen
X_test = np.array([[6], [7]])
y_pred = model.predict(X_test)
print("Vorhersagen für X_test:", y_pred)
# Visualisierung
plt.scatter(X, y, color='blue', label="Trainingsdaten")
plt.plot(X, y_train_pred, color='red', label="Regression")
plt.scatter(X_test, y_pred, color='green', label="Vorhersagen")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
plt.title("Lineare Regression Beispiel")
plt.show()Um die Güte des Modells anhand von MSE und R² zu bewerten habe ich das Beispiel so erweitert. dass die beiden Werte werden berechnet und ausgegeben werde.
Steigung (Koeffizient): 0.6 Achsenabschnitt (Bias): 2.2 Mean Squared Error (MSE): 0.47999999999999987 R2-Score: 0.6000000000000001 Vorhersagen für X_test: [5.8 6.4]
MSE
Der MSE quantifiziert die durchschnittliche Größe der Fehler zwischen den tatsächlichen (beobachteten) Werten und den vorhergesagten Werten des Modells. Der MSE ist immer eine positive Zahl. Ein niedriger MSE deutet darauf hin, dass die Vorhersagen des Modells im Durchschnitt nah an den tatsächlichen Werten liegen. Das Modell passt gut zu den Daten. Ein hoher MSE deutet darauf hin, dass die Vorhersagen des Modells im Durchschnitt weit von den tatsächlichen Werten entfernt liegen. Das Modell passt schlecht zu den Daten.
Beim MSE gibt es keine universellen „guten“ oder „schlechten“ Werte, weil der Wert des MSE stark von der Skala der Zielvariablen abhängt. Wenn man beispielsweise Werte zwischen 0 und 10 vorhersagt, wäre ein MSE von 5 schlecht. Wenn man jedoch Werte zwischen 10.000 und 100.000 vorhersagen, ist ein MSE von 500 gut.
Der MSE sagt die durchschnittliche Größe der quadrierten Vorhersagefehler. Ein niedrigerer Wert ist besser. Ob ein spezifischer Wert „gut“ oder „schlecht“ ist, kann nur beurteilt werden, indem man ihn im Kontext der Skala der vorhergesagten Variable und im Vergleich zu anderen Modellen oder einer Basislinie betrachtet.
R2-Score
Der R2-Score gibt an, wie gut das Modell die Schwankungen der Zielvariablen abbildet. Dabei liegt der R2-Wert typischerweise zwischen 0 und 1.
- Ein hoher R2-Wert bedeutet, dass ein großer Teil der Varianz der abhängigen Variable durch das Modell erklärt wird. Das Modell passt gut zu den Daten und die unabhängigen Variablen sind gute Prädiktoren für die abhängige Variable.
Beispiel: R2 = 1: Das Modell erklärt 100% der Varianz der abhängigen Variable. Die Vorhersagen liegen exakt auf den tatsächlichen Werten. - Ein niedriger R2-Wert bedeutet, dass das Modell nur einen kleinen Teil der Varianz der abhängigen Variable erklärt. Viele der Schwankungen in der Zielvariablen bleiben unaufgeklärt, was darauf hindeuten kann, dass die unabhängigen Variablen das Phänomen nicht gut beschreiben oder dass wichtige Einflussfaktoren im Modell fehlen.
Beispiel:
R2 = 0 – Das Modell hat keine Varianz in der abhängigen Variable. Es ist nicht besser, als einfach immer den Durchschnittswert der abhängigen Variable vorherzusagen.
Der R2 Wert kann auch negativ werden, wenn das Modell schlechter abschneidet als ein Modell, das den Durchschnitt der Zielvariable vorhersagt. Dies tritt z.B. auf, wenn das Modell völlig ungeeignet für die Daten ist. Auch beim R2 gibt es keinen universellen Schwellenwert für „gut“ oder „schlecht“. Die Beurteilung hängt stark vom Anwendungsbereich (Domäne) ab.
Vergleich von R2 und MSE:
| Merkmal | MSE (Mean Squared Error) | R2-Score (Bestimmtheitsmaß) |
| Was es misst | Die durchschnittliche Größe der quadrierten Vorhersagefehler | Der Anteil der Varianz der Zielvariable, der durch das Modell erklärt wird. |
| Einheit/Skala | Hat die quadrierte Einheit der Zielvariablen. Der Wert ist abhängig von der Skala der Daten. | Ist dimensionslos. Der Wert ist unabhängig von der Skala der Daten. |
| Interpretation | Zeigt die durchschnittliche Fehlergröße. Ein niedrigerer Wert ist besser. | Zeigt die Modellgüte relativ zur Gesamtvarianz. Ein höherer Wert ist besser. |
| Wertebereich | Immer ≥ 0. Kein oberes Limit, hängt von der Datenskala ab. | Typischerweise 0 bis 1, kann aber auch negativ sein. |
| Beziehung | Ein niedriger MSE führt oft zu einem höheren R2, aber die genaue Beziehung hängt von der Gesamtvarianz der Daten ab. | R2 = 1 – (MSE * n / SST), wobei n die Anzahl der Datenpunkte ist und SST die Summe der quadrierten Gesamtabweichungen. Es gibt also eine direkte mathematische Verbindung auf demselben Datensatz. |
| Verwendung | Nützlich, um die tatsächliche Fehlergröße in den Einheiten der Daten zu verstehen. Gut für den Vergleich von Modellen auf demselben Datensatz. | Nützlich, um die erklärende Kraft des Modells zu verstehen und wie gut es die Streuung der Daten erfasst. |
